\[\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\tx}{\text} \newcommand{\p}{\partial\,} \end{align*}\]

概论

运放有如下特点：

• high voltage gain
• high input impedance
• low output impedance

此外，还要考虑：

• speed
• output voltage swings
• power dissipation

我们一般用如下几个参数来描述运放。

• Gain
• Small-signal Bandwidth
  • unity-gain $f_u$
  • 3-dB frequency $f_{3-\tx{dB}}$
• Large-Signal Behavior
• Output Swing
• Linearity
• Noise and Offset: determine the minimum signal level that can be processed
• Supply Rejection
• Slew Rate: $V_\tx{out}$ 对时间的比值（输入阶跃，输出的最大斜率）

One-Stage Op Amps

Simple OTA

我们考虑下图中的 Simple OTA(operational transconductance amplifier)

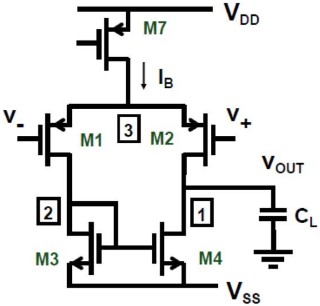
根据前几章的知识，我们容易求出：

\[A_v = g_{m1} \frac{r_O}{2}\] \[\tx{if } {\rm r_{O2}=r_{O4}=r_O} \tx{ then}\\ \tx{BW}=\frac{1}{2 \pi \dfrac{r_O}{2}(C_L+C_{n1})}\]

从而 $\tx{GBW}=\dfrac{g_{m1}}{2\pi(C_L+C_{n1})}$，$C_{n1}$ 指结点 1 处的电容。

这种结构的确定就是直流增益 $A_\tx{dc}$ 很难超过 40dB，所以我们采用下面的方法来增大输出电阻。

Telescopic Cascode Op Amps

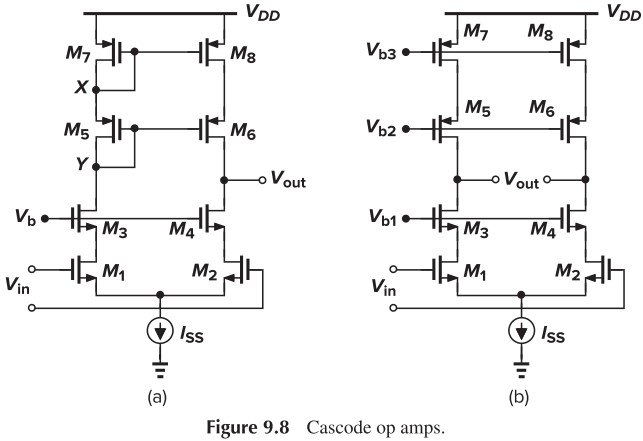
套筒式的优点就是输出阻抗放大了 $(g_m r_{DS})$ 倍，我们可以用下表来对比一下：

$$ \begin{aligned} A_v &= (g_m r_{DS})_1\\ R_\tx{out} &= r_{DS1} \end{aligned} $$	$$ \begin{aligned} A_v &= (g_m r_{DS})_1(g_m r_{DS})_2\\ R_\tx{out} &= r_{DS1}(g_m r_{DS})_2 \end{aligned} $$
$$ \tx{BW} = \frac{1}{2\pi R_\tx{out}C_L}\\ \tx{GBW} = \frac{g_{m1}}{2\pi C_L} $$
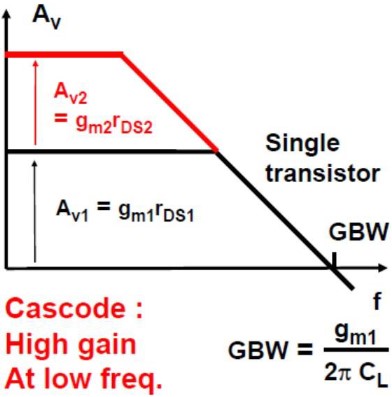注意纵轴取了 log，$A_{v1}$ 和 $A_{v2}$ 实际是相乘而非相加。

可以看出，虽然增益增大，但仅增大低频增益，带宽反而减小了。

另外，the output swings of telescopic cascode op amps are limited. 我们考虑 Fig. 9.8b，output swing 为 $2[V_{DD}-(V_{OD1}+V_{OD3}+V_{ISS}+\vert V_{OD5} \vert + \vert V_{OD7} \vert)]$（总电压减去 overdrive 电压和电流源电压，2 是源于差分）这种缺陷在输入与输出短接时会更明显。我们考虑 Fig. 9.9

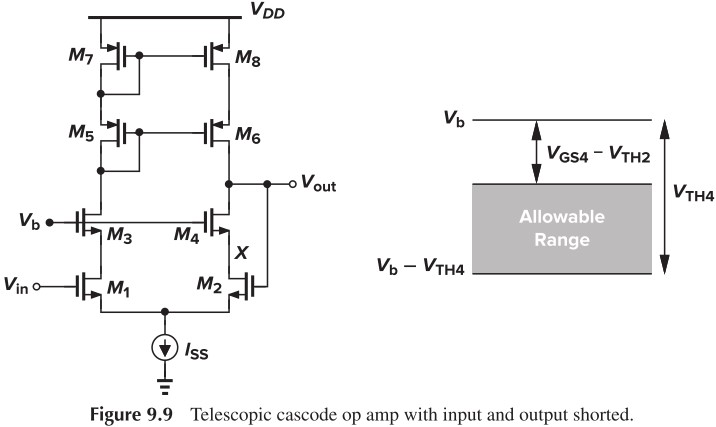
由于：

\[\begin{cases} V_\tx{out} \leq V_X + V_\tx{TH2}\\ V_\tx{out} \geq V_b-V_\tx{TH4}\\ V_X=V_b-V_{GS4} \end{cases}\\ \Rightarrow V_b-V_\tx{TH4} \leq V_\tx{out} \leq V_b-V_{GS4}+V_\tx{TH2}\\ \Rightarrow V_\max - V_\min = V_\tx{TH4}-(V_{GS4}-V_\tx{TH2})\]

可见输出摆幅进一步被限制了。

Folded-Cascode Op Amps

the drawbacks of telescopic cascode op amps:

• limited output swings
• difficulty in choosing equal input and output CM levels

In order to alleviate the drawbacks, a “folded-cascode” op amp can be used.

先对比大信号的特性。Two important differences between the two circuits in Fig. 9.14 are:

1. (b) requires more bias current than (a)
   • (a): $I_1,I_2$
   • (b): $I_{SS},I_1,I_2$ which means that (b) consumes more power.
2. (b) has a wider voltage swing, especially when input and output shorted.
   • (a): the input CM level cannot exceed $V_{b1}-V_{GS3}+V_\tx{TH1}$
   • (b): the input CM level cannot exceed $V_{b1}-V_{GS3}-\vert V_\tx{THP}\vert$

---

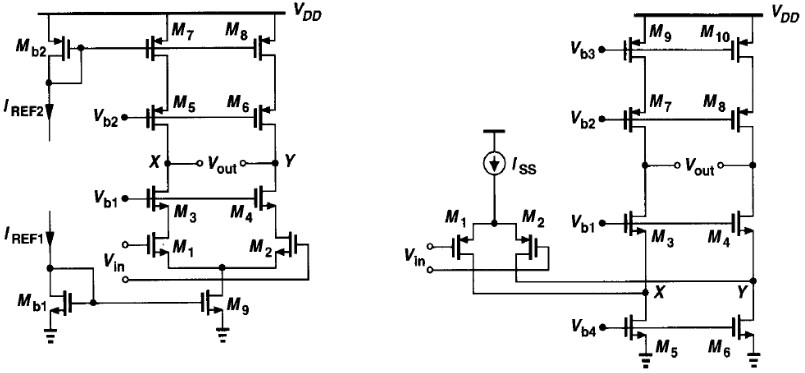
下面对比小信号增益。具体计算过程请看老师的 PPT，这里就不写了，反正都是用 $G_m R_\tx{out}$ 计算得出的。

\[折叠式：\\ \vert A_v \vert \approx g_{m1} \{[g_{m3}r_{O3}(r_{O1}\Vert r_{O5})] \Vert [g_{m7} r_{O7}r_{O9}]\}\\ 套筒式：\\ A_v \approx g_{m1}[(g_{m3}r_{O3}r_{O1})\Vert (g_{m5}r_{O5}r_{O7})]\]

注意到式中，折叠式多了一个 $r_{O1}\Vert r_{O5}$，另外，PMOS 的 $g_{m1}$ 也比 NMOS 小，这导致它的增益比套筒式小 2~3 倍。

---

另外，折叠式输入端的电容也会比套筒式大，导致极点更趋近于低频（见下图）。

---

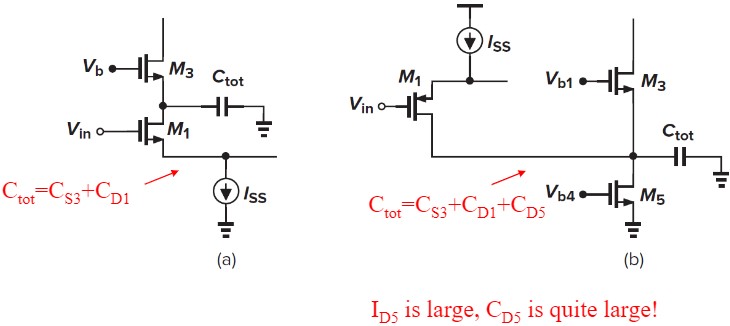
总结：the drawbacks of folded-cascode op amp:

• consumes more power 功耗大
• the gain is 2~3 times lower than telescopic cascode 增益小
• the pole is quite closer to the origin than that associated with the source of cascode devices in a telescopic topology 极点靠近原点，速度会变慢

为了增大电压摆幅，就不得不忍受这些缺点😕。

Two-Stage Op Amps

为了克服前面 one-stage op amps 的种种缺点，我们可以用 two-stage op amps. 第一个 stage 用来提供高增益，可以采用之前学过的各种高增益电路；第二个 stage 用来增大摆幅，一般采用简单的 CS stage。

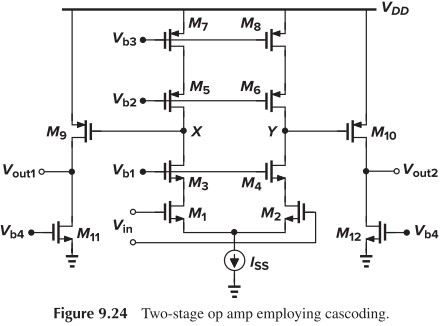
以 Fig. 9.24 的电路为例，它的增益如下：

\[A_v \approx {g_{m1,2}[(g_{m3,4}+g_{mb3,4})r_{O3,4}r_{O1,2}]\Vert (g_{m5,6}+g_{mb5,6})r_{O5,6}r_{O7,8}}\\ \times [g_{m9,10}(r_{O9,10}\Vert r_{O11,12})]\]

输出电压摆幅为 $V_{DD}-\vert V_{OD9,10}\vert-V_{OD11,12}$

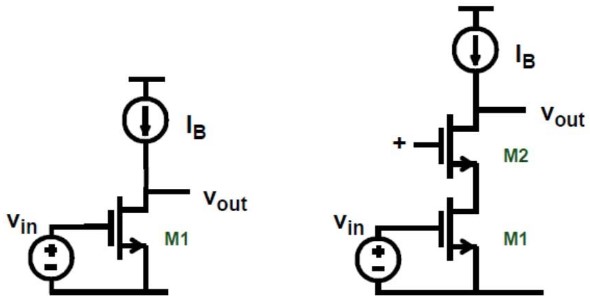
Gain Boosting

Basic Idea

One-Stage Op 的增益不够，Two-Stage Op 的速度又太慢了（电容太大），为了解决这些问题，我们又提出了 Gain Boosting. 它的原理如下：在单个 CS Stage 前面再加一个放大器，并且将反相输入端和 S 是连在一起的

我们可以轻松算出增益为 $-A_1g_mr_O$，也就是说，原本的跨导只有 $g_{m}$，现在增大到了 $A_1g_m$

我们可以将这个结构看成是一个更牛逼的 MOS 管，并放到之前的电路中，比如下图中的 degenerated stage

容易算出 $V_{GS} = (V_\tx{in}-R_SI_\tx{out})A_1 - R_S I_\tx{out}$ 且 $I_\tx{out}=g_m V_{GS}$，则：

\[G_m = \frac{I_\tx{out}}{V_\tx{in}}=\frac{A_1g_m}{1+(A_1+1)g_m R_S}\]

注意到式子中，分子中的 $g_m$ 增大了 $A_1$ 倍，而分母中的 $g_m$ 增大了 $(1+A_1)\approx A_1$ 倍。

$R_\tx{out}$ 的计算如下：$I_{r_O}=\dfrac{V_X-R_SI_X}{r_O}$，且 $I_0 = (-A_1R_SI_X-R_SI_X)g_m$，从而：

\[I_X = (-A_1R_SI_X-R_SI_X)g_m + \frac{V_X-R_SI_X}{r_O}\\ \Downarrow\\ R_\tx{out} = r_O+(A_1+1)g_m r_O R_S+R_S\]

由于 $G_m$ 和 $R_\tx{out}$ 均增大了，所以总的增益也增大了。

 考虑 Fig. 9.28 从源端看进去的电阻，计算过程与上面类似，在此直接给出结果： $$ R_X = \frac{R_D+r_O}{1+(A_1+1)g_m r_O} $$ 可以看出分母中的 $g_m$ 同样增大了 $(1+A_1)$ 倍。

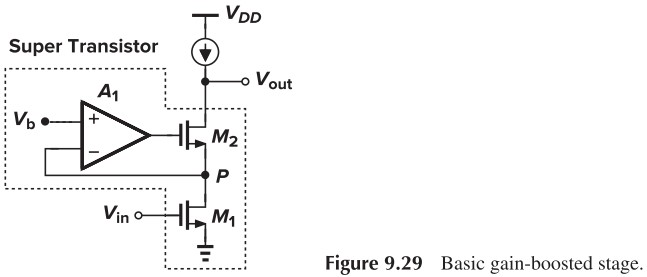
再来看一个例子，这次将 Gain Boost 放到输出管上（Fig. 9.29），它的输出电阻和之前 degenerated stage 是类似的，而由于 M2 的源端电阻很小（参考上面例题），所以 $r_{O1}$ 几乎不分流，$I_{D1}=g_m V_\tx{in}$ 全部流到输出端，从而：

\[\begin{aligned} \vert A_v \vert &\approx g_{m1}\left[ r_O+(A_1+1)g_m r_O R_S+R_S \right]\\ &\approx g_{m1}g_{m2}r_{O1}r_{O2}(A_1+1) \end{aligned}\]

看来 Gain Boost 用来放大输出电阻也挺好用的。

Circuit Implementation

虽然之前的 Gain Boost 都是用双端的 Op 来实现，但其实用单端的放大器就能实现。As shown in Fig. 9.32(a), if $I_1$ is ideal, then $\vert A_1 \vert=g_{m3}r_{O3}$, yielding $\vert A_v \vert \approx g_{m1}r_{O1}g_{m2}r_{O2}(g_{m3}r_{O3}+1)$

但 (a) 有一个坏处就是 P 点处的电压必须高于 $V_{GS3}$。为了增大摆幅，我们将 nmos 换成 pmos，即 Fig. 9.32(b)，这样的话增益不变，但 $V_P=V_{GS1}-V_{TH1}$。

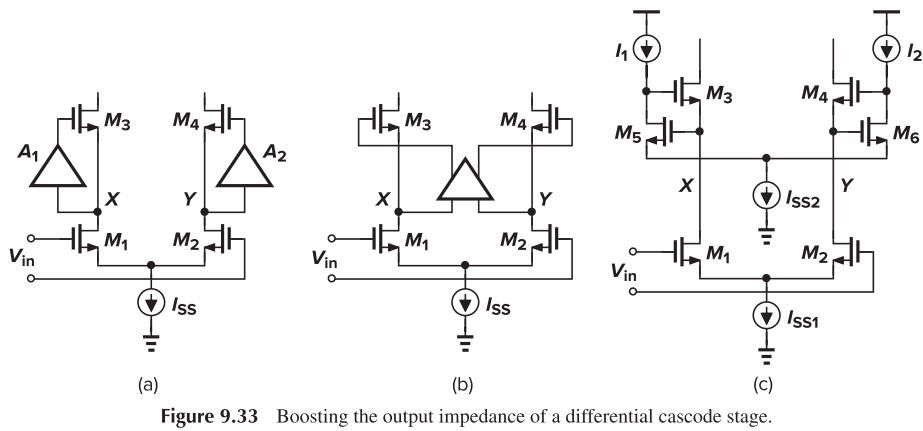
我们还可以进一步用在差分放大器上（Fig. 9.33），但具体分析我懒得写了。

Frequency Response

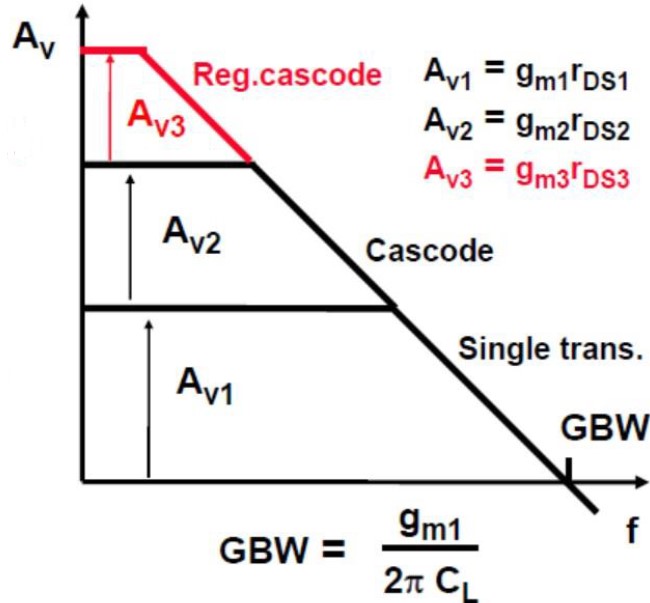
具体分析过程和之前分析频率响应是一样的，我这里就不写了，自己看书。从下图中可以看出 Gain Boosting 依然是增大增益、减小了带宽、GBW 不变。

小结

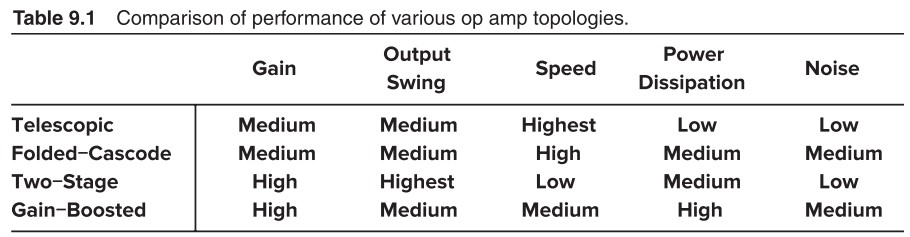
让我们回忆一下之前的内容：

我们嫌弃 CS Stage 的增益太小，于是用了 Cascode，多级 Cascode 就是 Telescopic，但是多级会消耗太多裕度，所以用了 Folded-Cascode，但 Folded-Cascode 只是消除了输入管的裕度损耗，堆叠的输出管还是会消耗很多裕度，所以我们又用了 Two-Stage 来减小输出管的裕度损耗，同时也进一步增大了增益。但 Two-Stage 的速度又不够快，所以又用了 Gain-Boosted 实现高增益且速度较快。

可以看出，有得必有失。当我们解决一个问题时，另一个问题就会冒出来，所以要权衡得失。

吐槽：上表中最菜的就是 Folded-Cascode，摆幅没提高多少，速度和功耗反而没 Telescopic 好。那我们为什么要学啊(╯‵□′)╯︵┻━┻

Common-Mode Feedback

Basic Concept

下面先来说说什么是 common-mode feedback (CMFB)，为了让共模输出稳定，我们构造如下的共模反馈电路：

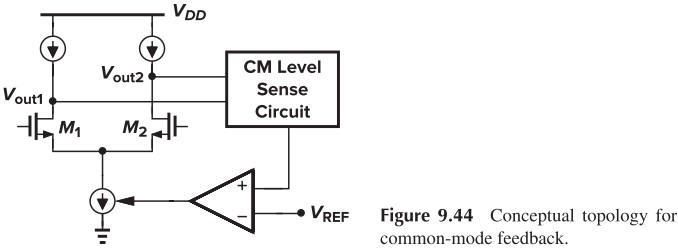
反馈电路包括三部分：

• sensing the output CM level
• comparison with a reference
• returning the error to the amplifier’s bias network

前两个还好理解，但第三个为什么反馈回 $I_{SS}$ 能使共模输出稳定呢？我们考虑下面这个 differential negative feedback

由于电流镜会存在误差，所以不可避免地，$I_{D3,4}\neq \frac{I_{SS}}{2}$，那么在 $X,Y$ 处，为了使上下电流相匹配，那么就会出现两种情况：

• $I_{D3,4}>\frac{I_{SS}}{2}$, M3 and M4 enter the triode region so that their drain currents fall to $I_{SS}/2$
• $I_{D3,4}<\frac{I_{SS}}{2}$, M5 enters the triode region, thereby producing only $2I_{D3,4}$

任意一种情况都是不我们希望的，所以我们需要调整 $I_{SS}$ 使其与 $I_{D3,4}$ 相匹配。

于是我们提出下图中的电路，其中，$R_1,R_2$ 负责获取共模电平，然后通过运放控制下面的偏置电流（当然，控制 $I_{SS}$ 也是可以的）。