\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}}
\newcommand{\bd}{\boldsymbol}
\newcommand{\tx}{\text}
\newcommand{\L}{\mathscr{L}}
\newcommand{\p}{\partial\,}
\end{align*}\]
- Among the output noise and the input-referred noise, which one is more popular to be used in the circuit simulation? Why?
Devices are often specified with input-referred noise, because, with an amplifier for example, the output noise will depend on gain so is not constant.
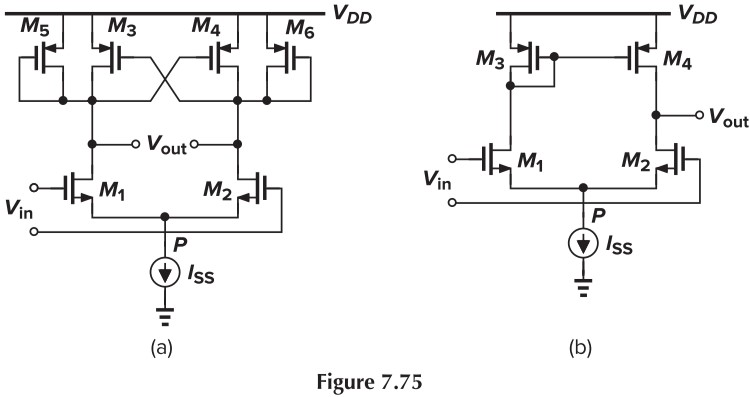
7.12 Assuming that $λ = γ = 0$, calculate the input-referred thermal noise voltage of each circuit in Fig. 7.75. For part (a), assume that $g_{m3,4} = 0.5g_{m5,6}$.

解:(a)
\[\begin{aligned} |A_v| &= g_{m1,2}R_\tx{out}\\ \overline{V_{n,\tx{out}}^2} &= 4kT \gamma (2g_{m1,2}+2g_{m3,4}+2g_{m5,6}) R_\tx{out}^2\\ &= 4kT \gamma (2g_{m1,2}+3g_{m5,6}) R_\tx{out}^2\\ \overline{V_{n,\tx{in}}^2} &= 4kT \gamma (\frac{2}{g_{m1,2}}+\frac{3g_{m5,6}}{g_{m1,2}^2}) \end{aligned}\](b) The input-referred noise voltage of the five-transistor OTA is the same as that of the fully-differential circuit.
\[\begin{aligned} G_m&=g_{m1,2}\\ \overline{I_{n,\tx{out}}^2} &= 4kT \gamma (g_{m1}+g_{m2}+g_{m3}+g_{m4})\\ \overline{V_{n,\tx{in}}^2} &= \frac{\overline{I_{n,\tx{out}}^2}}{G_m^2} = 4kT\gamma \left(\frac{2}{g_{m1,2}}+\frac{2g_{m3,4}}{g_{m1,2}^2}\right) \end{aligned}\]