SCUTEEE

电流镜

\[\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\tx}{\text} \newcommand{\L}{\mathscr{L}} \newcommand{\p}{\partial\,} \end{align*}\]

Basic Current Mirrors

Current source 很有用，前几章中电流源有如下作用：

  • 为电路提供合适的静态工作点
  • 起一个大电阻的作用，但不消耗过多的电压 裕度
  • 工作在饱和区的MOS管可以当作电流源

但怎么使得 MOSFET operate as a stable current source? 最简单的，就是用 resistive bias (Fig. 5.2)

Figure 5.2 Definition of current byresistive divider
\[I_\tx{out} \approx \frac{1}{2} \mu_n C_\tx{ox} \frac{W}{L} \left(\frac{R_2}{R_1+R_2}V_{DD}-V_\tx{TH}\right)\]

但式中的 $\mu_n,V_\tx{TH},R$ 都是会随温度变化的，所以这种方法并不可靠。

实际在电路中，有一个标准电流源 $I_\tx{REF}$（在 Chapter 12 会介绍），我们可以用利用 $I_\tx{REF}$ 复制出其他电流源：

  • 利用 $I_D$-$V_{GS}$ 关系，令 $I_D=I_\tx{REF}$，得到固定的 $V_{GS}$（Fig. 5.5a）
    • 我们之前都是 $V_{GS}$ 决定 $I_D$，这里是反过来的
    • 但这要求 MOS 是 dioded connected（保证它处在饱和区）
  • 将 $V_{GS}$ 作为另一个管子的 $V_{GS}$，得到 $I_\tx{out}$（Fig. 5.5b）
Figure 5.5(a) Diode-connected deviceproviding inverse function; (b) basic current mirror

Fig. 5.5(b) 就是 电流镜 current mirror。公式表述为：

\[\begin{aligned} I_\tx{REF} &= \frac{1}{2} \mu_n C_\tx{ox} \left(\frac{W}{L}\right)_1(V_{GS}-V_\tx{TH})^2\\ I_\tx{out} &= \frac{1}{2} \mu_n C_\tx{ox} \left(\frac{W}{L}\right)_2(V_{GS}-V_\tx{TH})^2 \end{aligned}\]

从而：

\[I_\tx{out} =\frac{(W/L)_2}{(W/L)_1} I_\tx{REF}\]

find the drain current of $M_4$ if all of the transistors are in saturation.

FIgure 5.7

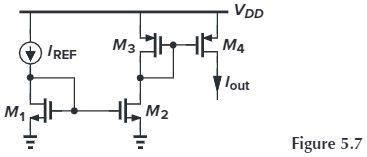
首先，$I_{D2}=\frac{(W/L)_2}{(W/L)_1} I_\tx{REF}$，然后，$I_{D4}=\frac{(W/L)_4}{(W/L)_3} I_{D3}$，所以 $I_{D4}=\alpha\beta I_\tx{REF}$，$\alpha,\beta$ 是对应的 $W/L$ 比例
我们只需要记住 $I_D$ 与 $(W/L)$ 成比例即可。
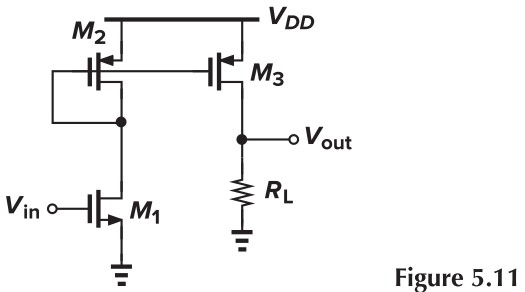
另外注意到电流镜对电流有缩放的作用，利用这点可以提高增益（如下 Fig. 5.11）

Figure 5.11

当尺寸缩小时，$W/L$ 很难精确控制（因为 $L_\tx{eff} = L_\tx{drawn} - 2L_D$，$L_D$ 会导致误差），此时我们可以采用多管并联/串联的方式来调整 W 或 L（Fig. 5.10）

Figure 5.10 Current mirrors providing IREF div 2 from IREF by (a) half-width device and (b) series transistors

Cascode Current Mirrors

上面看起来很美好，但如果考虑上沟道长度调制效应：

\[\begin{aligned} I_{D1} &= \frac{1}{2} \mu_n C_\tx{ox} \left(\frac{W}{L}\right)_1(V_{GS}-V_\tx{TH})^2(1+\lambda V_{DS1})\\ I_{D2} &= \frac{1}{2} \mu_n C_\tx{ox} \left(\frac{W}{L}\right)_2(V_{GS}-V_\tx{TH})^2(1+\lambda V_{DS1}) \end{aligned}\]

就会发现：

\[\frac{I_{D2}}{I_{D1}}=\frac{(W/L)_2}{(W/L)_1}\cdot \frac{1+\lambda V_{DS2}}{1+\lambda V_{DS1}}\]

$V_{DS1}=V_{GS1}$ 是个恒定值，但 $V_{DS2}$ 却可能会变。为了抑制这种效应，我们有两种方法：

  • 方法一：令 $V_{DS2}=V_{DS1}=V_{GS1}$
  • 方法二：令 $V_{DS1}=V_{DS2}$

当然啦，我们并不是把对应点直接连起来，而是令上面电压尽可能接近。

方法一

Figure 5.12 Cascode current source

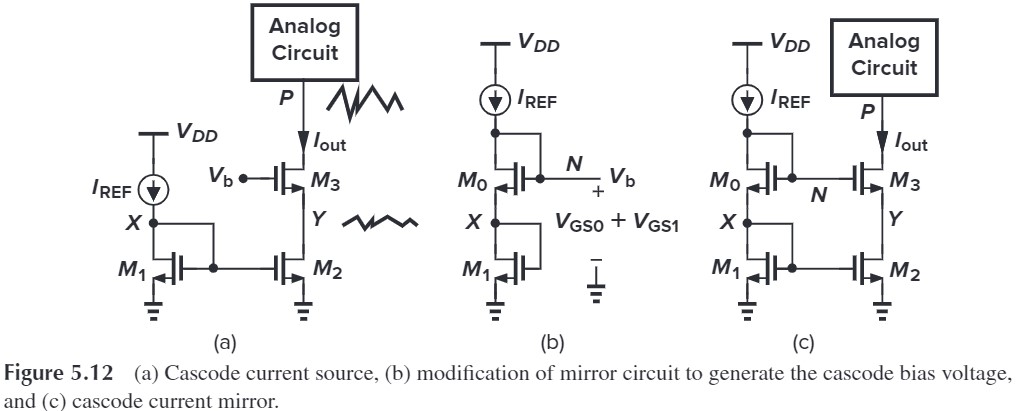
Cascode device can shiel a current source, thereby reducing the voltage variations across it (Fig. 5.12a) To ensure $V_{DS2}=V_{DS1}$, we must generate $V_b-V_{GS3}=V_{DS1}(=V_{GS1})$, i.e $V_b=V_{GS3}+V_{GS1}$. By adding $M_0$, we have $V_b = V_{GS0}+V_{GS1}$ (Fig. 5.12c), therefore $V_Y=V_X$

补充：对宽长比的要求：$L_2=L_1$，$L_3=L_0$，$W_3/W_0 = W_2/W_1$（利用多管并联来提高精确度）

We can plot $I_X$ s $V_X$ drops:

Figure 5.15

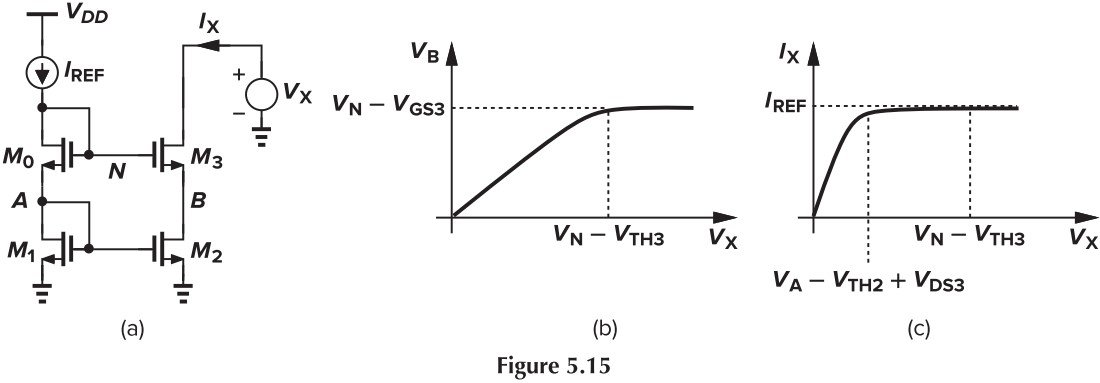
这种方法的优点是：阻抗高、输出电流值精确，但这是以牺牲电压裕度为代价的。我们可以比较一下 Fig. 5.14 (a) 和 (b) 的电压裕度：

Figure 5.14 headroom consumed by a cascode mirror

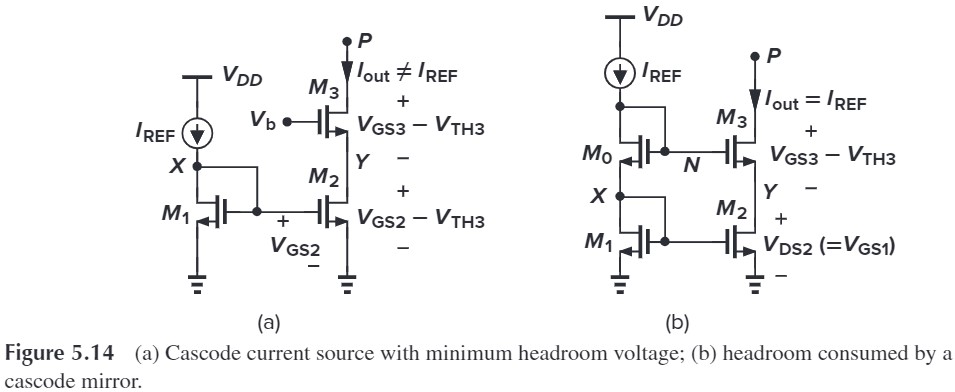
For simplicity, 忽略 body effect, 并假设 all of the transistors are identical. 那么，$P$ 处的最小电压为：

  • (a) $V_P=(V_{GS3}-V_\tx{TH})+(V_{GS2}-V_\tx{TH})$
  • (b) $V_P=V_N - V_\tx{TH}\(=V_{GS0}+V_{GS1}-V_\tx{TH}\)=(V_{GS0}-V_\tx{TH})+(V_{GS1}-V_\tx{TH})+V_\tx{TH}$

这两者的差异在于，(a) 中电压必须走 $Y$ 支路，从而必须有 $V_Y=V_{GS2}-V_\tx{TH}$；而 (b) 中电压可以走另一条路 $X$，从而 $V_X=V_{GS1}$，这样就少减了个 $V_\tx{TH}$，裕度就减少了。

那么我们为啥不用 (a) 呢？因为 (a) 不能保证 $M_1$, $M_2$ 的 $V_{DS}$ 相等，我们必须让 $V_b$ track $V_{GS3}+V_{DS2}$（即 $V_{GS3}+V_{DS1}=V_{GS3}+(V_{GS1}-V_\tx{TH})$）。那么有办法实现这一点吗？下面我们来讨论一下。

方法二

注意到 Fig. 5.14 (a) 中，我们要让 $V_X=V_Y=V_{GS2}-V_\tx{TH}$，即 $V_{DS1}=V_{GS2}-V_\tx{TH}$。However，Since $M_1$ is a diode-connected device, it appears impossible to expect a $V_{DS1}$ less than one threshold. 于是我们采用 Fig. 5.16(a) 中电路，令 $I_\tx{REF}R_1=V_\tx{TH}$，那么我们就有 $V_{DS1} = V_{GS1}-I_\tx{REF}R_1=V_{GS1}-V_\tx{TH}$，但由于 $R$ 可能会变，这种方式并不精确。

Figure 5.16 (a) Use of IR drop to improve accuracy of current mirror, (b) generation of Vb, and (c) alternative generation of Vb

那么我们可以换种方式，见 Fig. 5.18a，我们把电阻换成 MOS 管，那么，$V_{DS1}=V_{GS1}-V_{DS0}$，效果好像差不多诶！

Figure 5.18 Modification of cascode mirror for low-voltage operation

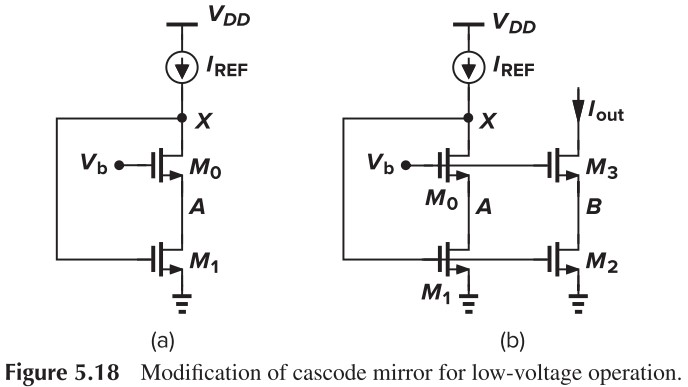
然后我们再将 $V_b$ 连在一起（Fig. 5.18），这么一来，$V_A=V_B=V_b-V_\tx{TH}$，就保证了 $V_{DS1}=V_{DS2}$

$V_b$ 的取值要保证 $M_0$，$M_1$ 都饱和，即：

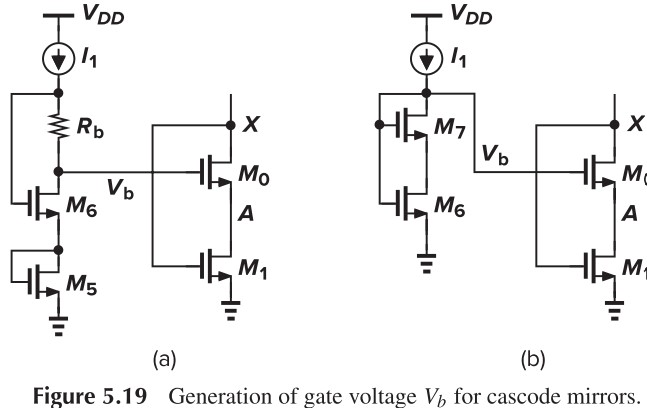
\[\begin{cases} V_b - V_\tx{TH0} \leq V_X = V_{GS1}\\ V_{GS1}-V_\tx{TH1}\leq V_A = V_b - V_{GS0} \end{cases}\\ \Downarrow\\ V_{GS0}+(V_{GS1}-V_\tx{TH1})\leq V_b \leq V_{GS1}+V_\tx{TH0}\]

We can generate $V_b$ with the circuits in Fig. 5.19（具体分析咱就不说了）

Figure 5.19 Generation of gate voltage Vb for cascode mirrors

Active Current Mirrors

Differential Pair with Passive Load

Figure 5.23 (a) Differential pair with current-source load; (b) circuit for calculation of Gm; (c) circuit for calculation of Rout

这个电路没什么好说的，用电流源当负载，其增益计算如下：

\[\begin{aligned} |A_v| &= G_m R_\tx{out}\\ G_m &= \frac{I_\tx{out}}{V_\tx{in}}= g_{m1}\frac{V_\tx{in}}{2} \Big/V_\tx{in}=\frac{g_{m1}}{2}\\ R_\tx{out} &= r_{O4} \Vert \left[ r_{O2}+(1+g_{m2}r_{O2})(r_{O1}\Vert \frac{1}{g_{m1}})\right]\\ &\approx r_{O4} \Vert 2r_{O2} \end{aligned}\]

唯一要注意的是 $R_\tx{out}$ 的计算。另外说说这个电路的缺点：$M_1$ 那边的电流被浪费了，并且没有对增益作出贡献。

Differential Pair with Active Load

Five-transistor OTA 这个电路十分重要！！请好好学！

Figure 5.26 (a) Concept of combining the drain currents of M1 and M2, (b) realization of (a), and (c) response of the circuit to differential inputs

首先我们从感性上看看这个电路是如何工作的。假设输入了正的差分电压，即 $V_\tx{in1} \uparrow$，这会导致 $I_{D1}\uparrow$，电流源会将这个电流按比例 copy 到输出，从而 $V_\tx{out}=I_{D1}(r_{O2}\Vert r_{O4})$ 会增大；同时，$V_\tx{in2}\downarrow$，$I_{D2}\downarrow$，从而共源输出 $V_\tx{out}=I_{D2}(r_{O2}\Vert r_{O4})$ 也会增大。这么一来，在两边作用下，增益为为 $g_m(r_{O2}\Vert r_{O4})$

Large-Signal Analysis

Figure 5.27 Differential pair with active current mirror a
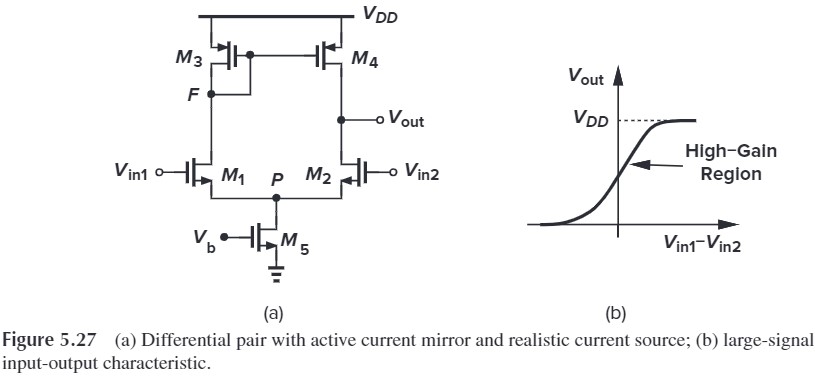
  • 正常情况下，五管均应该饱和
  • 若 $V_\tx{in1}\gg V_\tx{in2}$，那么 $M_1$ 关闭，那么 $M_3$ 也不会有电流，$M_3$ 要么是饱和要么关闭，而由于没有电流，所以只能是关闭，因此 $V_F=V_{DD}$。因此 $M_4$ 也关闭，从而 $V_\tx{out}=0$。此时 $M_2,M_5$ is in deep triode region
  • 类似的，若 $V_\tx{in2}\gg V_\tx{in1}$，那么 $M_2$ 关闭，$I_{D2}=0$，从而 $M_4$ is in deep triode region，$V_\tx{out}=V_{DD}$。此时 $M_1,M_3,M_5$ 均饱和。

For $M_2$ to be saturated, $V_\tx{out}$ cannot be less than $V_\tx{in,CM}-V_\tx{TH}$. Thus, to allow maximum output swings, minimum CM level is given by $V_{GS1,2}+V_{DS5,\tx{min}}$

If $V_\tx{in1}=V_\tx{in2}$, the CM output is $V_\tx{out}=V_F=V_{DD}-\vert V_{GS3} \vert$

Small-Signal Analysis

Approximate Analysis

We simply use the lemma $\vert A_v \vert = G_m R_\tx{out}$ to calculate the gain.

For the calculation of $G_m$, consider Fig. 5.32. The current producted by $M_1$ is copied to $I_\tx{out}$ by current mirror. Therefore, $I_{D1}=\vert I_{D3}\vert = \vert I_{D4}\vert = g_{m1,2}V_\tx{in}/2$ and $I_{D2}=-g_{m1,2}V_\tx{in}/2$. yielding $I_\tx{out}=-g_{m1,2}V_\tx{in}$ and hence $\vert G_m \vert = g_{m1,2}$

Figure 5.32 (a) Circuit for calculation of Gm; (b) circuit of (a) with node P grounded
Figure 5.33 (a) Circuit for calculating Rout; (b) substitution of a resistor for M1 and M2

To calculate $R_\tx{out}$, we use the circuit in Fig. 5.33. We replace $M_1,M_2$ with $R_{XY}=2r_{O1,2}$, and the current on it is

\[I_{1,2}=\frac{V_X}{2r_{O1,2}+(1/g_{m3})\Vert r_{O3}}\]

We multiply this current by $(1/g_{m3})\vert r_{O3}$ to obtain the gate-source voltage of $M_4$ and then multiply the result by $g_{m4}$. It follows that

\[I_X = \frac{V_X}{2r_{O1,2}+(1/g_{m3})\Vert r_{O3}}\left[ 1+\left(\frac{1}{g_{m3}}\Vert r_{O3}\right)g_{m4} \right]+\frac{V_X}{r_{O4}}\]

For $2r_{O1,2}\gg (1/g_{m3})\Vert r_{O3}$, we have

\[R_\tx{out} \approx r_{O2} \Vert r_{O4}\]

The overall voltage gain is approximately equal to $\vert A_v \vert = G_m R_\tx{out} = g_{m1,2}(r_{O2}\Vert r_{O4})$

Exact Analysis

就是用小信号模型求解，此处仅给出结果：

\[\vert A_v \vert = g_{m1,2}(r_{O2}\Vert r_{O4}) \frac{2g_{m4}r_{O4}+1}{2(g_{m4}r_{O4}+1)}\]

就是之前的结果乘上一个系数。

    This is a free website. If you want to support us, please share our website with others!
    © SCUTEEE 2020, All Rights Reserved.
    搜索