\[\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\tx}{\text} \newcommand{\p}{\partial\,} \end{align*}\]

General Considerations

In summary, if a negative-feedback circuit has a loop gain that satisfies two conditions:

\[\begin{aligned} \vert H(j\omega_0) \vert &\geq 1\\ \angle H(j\omega_0) &= 180^\circ \end{aligned}\]

For the oscillation to begin, a loop gain of unity or greater is necessary.

Ring Oscilators

A ring oscillator consists of a number of gain stages in a loop. We start from single-stage feedback to multi-stage feedback.

电路一

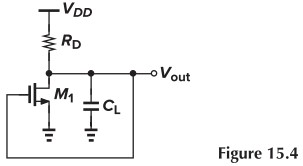
From Fig. 15.4, the open-loop circuit contains only one pole, thereby providing a maximum frequency dependent phase shift of $90^\circ$ (at a frequency of infinity). Added by a dc phase shift of $180^\circ$, the max total phase shift is $270^\circ< 360^\circ$. The loop therefore fails to sustain oscillation growth.

电路二

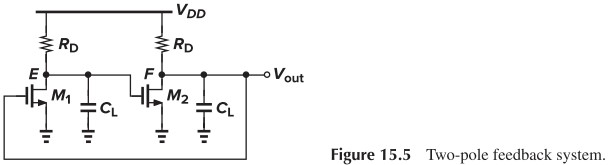
• two pole → $180^\circ$
• dc phase shift → $360^\circ$

the circuit achieve a total phase shift of $360^\circ$ at DC. As a result, it simply “latches up” rather than oscillates.（即反馈导致 $V_E$ 电压不断上升，直到固定到 $V_{DD}$）

电路三

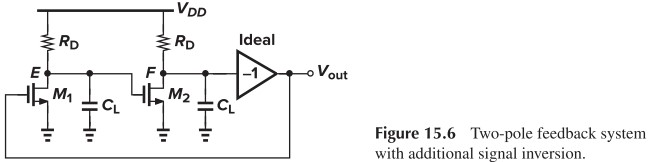
• dc phase shift → $540^\circ$
• two pole → $180^\circ$

The frequency-dependent phase shift can reach $180\circ$ at a frequency of infinity. Since the loop gain vanishes at very high frequencies, we observe that the circuit does not satisfy both of Barkhausen’s criteria at the same frequency.

电路四

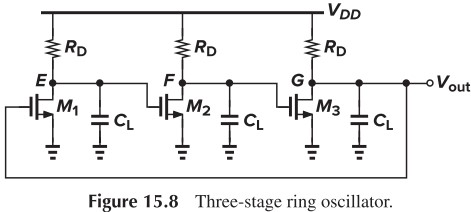
• dc phase shift → $540^\circ$
• two pole → $270^\circ$

The total phase shift around the loop $\phi$ equals $-180^\circ$ at $\omega<\infty$. This circuit indeed oscillates if the loop gain is sufficient.

从上面几个案例，我们可以总结如下分析步骤：

1. 判断 dc phase shift
2. 判断 pole 带来的 phase shift
3. 把 1 和 2 相加，看在 $(0,\infty)$ 内 total phase shift 能否够 360 （并且 360 时不能在 0 或 $\infty$）
4. 判断在 360 时 gain 是否大于等于 1

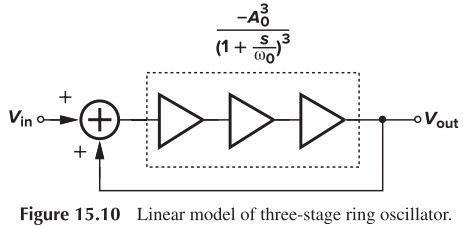
下面我们继续分析最后一个 3 级振荡器，我们还需要考虑增益。设每一级的传输函数为 $\dfrac{-A_0}{1+s/\omega_0}$，则 loop gain 为：

\[H(s) = -\frac{A_0^3}{(1+\dfrac{s}{\omega_0})^3}\]

要使相移达到 $180^\circ$，则每一级贡献 $60^\circ$，即：

\[\arctan \frac{\omega_\tx{osc}}{\omega_0} = 60^\circ\\ \Rightarrow \omega_\tx{osc} = \sqrt{3} \omega_0\]

代入 loop gain，得到：

\[\frac{A_0^3}{\left[\sqrt{1+(\dfrac{\omega_\tx{osc}}{\omega_0})}\right]^3} = 1\\ \Rightarrow A_0 = 2\]

总结, a three-stage ring oscillator requires a low-frequency gain of 2 per stage, and it oscillates at a frequency of $\sqrt{3} \omega_0$, where $ω_0$ is the 3-dB bandwidth of each stage

LC Oscillators

Basic

我们先来回顾一下电路与高频的知识。

对于 LC 并联电路，我们有：

\[Z = \frac{1}{j\omega C+\dfrac{1}{j\omega L}}\]

当 $j\omega C = \dfrac{1}{j\omega L}$，即 $\omega = 1/\sqrt{LC}$ 时，$Z=\infty$，此时为谐振状态（电路的知识）

---

考虑上电感的电阻

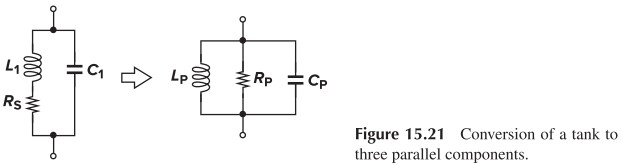
对于 Fig. 15.21a，

\[Z = \frac{(R + j \omega L) \frac{1}{j\omega C} }{ R + j(\omega L - \frac{1}{\omega C})}\]

当 $\omega = 1/\sqrt{LC}$ 时，$Z$ 达到最大值 $\dfrac{L}{CR}$。完整的幅频特性如下图所示：

有时候我们希望电阻也是并联的，这样好算一点。转换的方法如下（具体推导过程略）

\[C_p=C_1\\ L_p=L_1\\ R_p \approx \frac{L_1^2 \omega^2}{R_S} =Q^2 R_S\\\]

转换成并联后，我们可以写出其 $Q$ 值为 $Q_p = \dfrac{R_p}{\omega_p L}=R_p \omega_p C= R_p \sqrt{\dfrac{C}{L}}$

Cross-Coupled Oscillator

我们将 LCR 振荡网络作为负载。当只有一级时，CS 贡献 $180^\circ$，RLC 贡献 $-90^\circ\sim 90^\circ$，加起来不够 $360^\circ$

如果再增加一级，CS 贡献 $360^\circ$，RLC 贡献 $-180^\circ\sim 180^\circ$，那么在谐振频率处刚好是 $360^\circ$，可以起振。注意对比之前 2 级反相的情况，由于之前的 0 相移在 DC，所以被锁定，无法振荡。

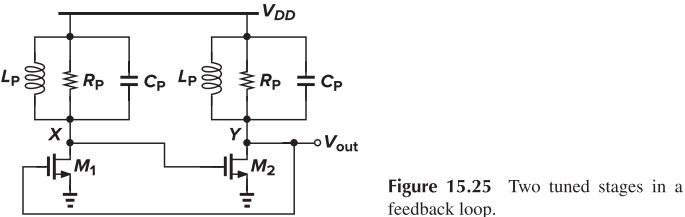
我们从另一个角度来理解为什么上面这种解法可以振荡。我们将电路整理一下就会发现，下面两个MOS组成了负阻（前面某道练习题有说），负阻抵消了振荡的电阻损耗，使得振荡可以维持下去。

下面我们来详细研究一下这个负阻结构。

考虑 Fig. 15.33b 的小信号模型，有：

\[\begin{cases} V_X - V_1 + V_2 = 0\\ I_X = g_{m2}V_2 = - g_{m1}V_1 \end{cases}\\ \Rightarrow V_X + \frac{I_X}{g_{m1}} + \frac{I_X}{g_{m2}} = 0\\ \Rightarrow \frac{V_X}{I_X} = -\frac{1}{1/g_{m1}+1/g_{m2}}\]

若 $g_{m1}=g_{m2}=g_m$，则这个电路具有一个负阻 $-\dfrac{2}{g_m}$。

要让 $-\dfrac{2}{g_m}$ 抵消两个 $R_P$，则 $g_m = \frac{1}{R_P}$，此时的差分增益为 $g_m R_P = 1$，这也是差分增益的最小要求。

---

另一种负阻结构如下图所示：

根据小信号模型容易写出：

\[V_X = (I_X - \frac{-I_X}{C_1 s}g_m) \frac{1}{C_2 s}+\frac{I_X}{C_1 s}\\ \Rightarrow \frac{V_X}{I_X}=\frac{g_m}{C_1 C_2 s^2}+\frac{1}{C_2 s}+\frac{1}{C_1 s}\]

注意到第一项是负的（$s^2=-\omega^2$），所以 Fig. 15.17c 的结构是可以振荡的。

Colpitts Oscillator

详细分析看书，我这里只是简单说一下。首先我们需要把这个看作一个 CG Stage，输出的电压经过电容分压后再放大 $g_m R_D$ 倍（忽略 $g_{mb}$），以弥补 $R_P$ 的损耗。其振荡频率为：

\[\omega_R^2 = \frac{1}{L_P C}\\ C=\frac{1}{1/C_1+1/C_2}\]

而放大倍数需要满足：

\[g_m R_P = \frac{(C_1+C_2)^2}{C_1C_2}\]

关于这个式子的来源嘛，书上列举了一大堆公式，你可以去看一下。我们一般把这个表示为 $\frac{C_1}{C_2}$ 的函数，即：

\[g_m R_P = \frac{C_1}{C_2}(1+\frac{C_2}{C_1})^2 \geq 4\\\]

最小值可以在 $\frac{C_1}{C_2} = 1$ 时取得.

相关论文：Output voltage analysis for the MOS Colpitts oscillator

Voltage-Controlled Oscillators

现在我们想要让电压能控制频率，而要改变谐振频率，则必须改变 L 或 C，由于电感很难改变，所以我们必须用0可变电容。在半导体器件中，我们知道二极管两边的反偏电容会随着电压改变，即：

\[C_\tx{var} = \frac{C_0}{(1+\dfrac{V_R}{\phi_B})^m}\]

电路图见 Fig. 15.53

---

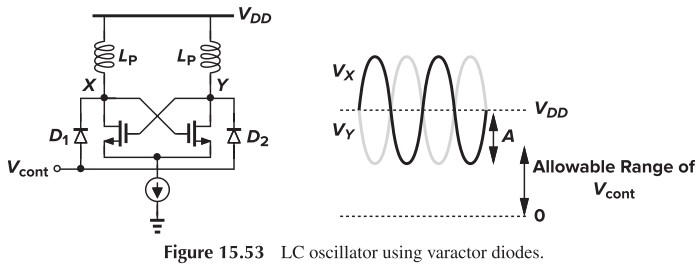
对于 Ring Oscillators，对于 N 个反相器组成的延时电路，其振荡频率是 $(2NT_D)^{-1}$。我们可以通过改变反相器的延时时间来改变周期，具体电路如下：

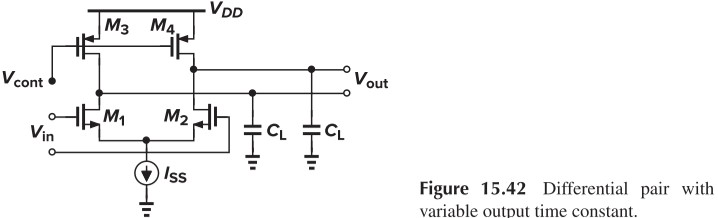
其中，M3、M4 处于深度线性区，对应的 RC 延时为：

\[\begin{aligned} \tau &= R_{3,4} C_L\\ &=\frac{C_L}{\mu_p C_\tx{ox} (\frac{W}{L})_{3,4}(V_{DD}-V_\tx{cont}-\vert V_\tx{THP}\vert)} \end{aligned}\]

Mathematical Model of VCOs

我们知道，相位是频率的积分，频率是相位的微分（就像速度和路程一样），那么，当频率变快时，相位的积累速度就会变快。可以参考下面这幅图：

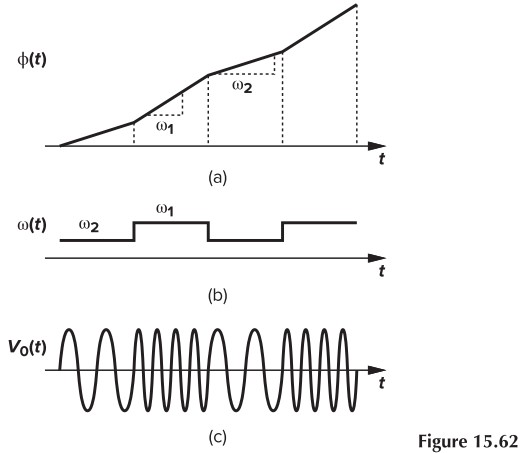
用公式表述如下：

\[\begin{cases} \phi = \int \omega \dif t + \phi_0\\ \omega_\tx{out}=\omega_0 + K_{VCO}V_\tx{cont} \end{cases}\] \[\begin{aligned} V_\tx{out}(t) &= V_m \cos\left( \int \omega_\tx{out} + \phi_0 \right)\\ &=V_m \cos (\omega_0 t+K_{VCO}\int V_\tx{cout} \dif t+\phi_0) \end{aligned}\\ \Rightarrow\phi_{ex} = K_{VCO} \int V_\tx{cont} \dif t\\ \Rightarrow\frac{\phi_{ex}}{V_\tx{cont}}(s) = \frac{K_{VCO}}{s}\]

从公式中可以看出，VCO 实际上是一个积分器！为什么要说这个呢？因为后续我们可能需要对系统进行建模，需要求出系统函数（也就是信号与系统中学的拉普拉斯变换啦！忘了的同学可以去看本站的相关笔记）。