\[\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\tx}{\text} \newcommand{\p}{\partial\,} \end{align*}\]

Basic Idea of Reference

集成电路中会用到很多基准电压，比如：

1. Supply-independent biasing
2. Proportional to absolute temperature (PTAT) reference
3. Constant-Gm behavior reference
4. Temperature independent reference

为啥要这么多基准呢？理想情况下，我们希望基准电压（1）不受 supply 影响；（2）不受温度影响。但遗憾的是，我们无法满足所有要求，所以只能分别满足要求。

Supply-Independent Biasing

In previous chapters of current mirrors, we has implicitly assumed that a $I_\tx{REF}$ that does not vary with $V_{DD}$ is available. In this chapter, we will discuss how to generate $I_\tx{REF}$

Solution1: use a resistor (Fig. 12.1b) to generate a $I_\tx{REF} = \dfrac{V_{DD}}{R_1+1/g_{m1}}$. Obivously, it’s sensitive to $V_{DD}$, so it doesn’t work.

Solution2: make $I_\tx{REF}$ be a replica of $I_\tx{out}$ (Fig. 12.2) $I_\tx{REF}$ is bootstrapped（引导、自举）to $I_\tx{out}$, i.e. $I_\tx{out} = KI_\tx{REF}$

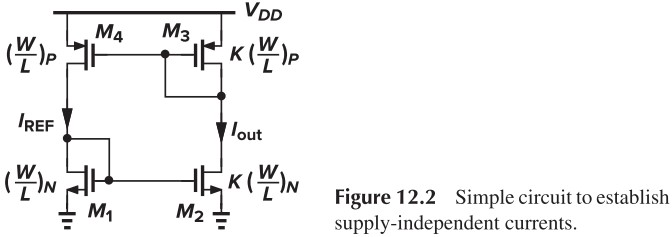
How do we calculate these currents? If $M_1$–$M_4$ operate in saturation and $λ ≈ 0$, than any current is possible! To uniquely define the currents, we add another constraint to the circuit (Fig. 12.3a)

\[\begin{aligned} V_{GS1} &= V_{GS2}+I_{D2}R_S\\ \sqrt{\dfrac{2I_\tx{out}}{\mu_n C_\tx{ox}(W/L)_N}}+V_\tx{TH1} &= \sqrt{\dfrac{2I_\tx{out}}{\mu_n C_\tx{ox} K (W/L)_N}} + V_\tx{TH2} + I_\tx{out} R_S\\ &\Downarrow \tx{if } V_\tx{TH1} = V_\tx{TH2}\\ \sqrt{\dfrac{2I_\tx{out}}{\mu_n C_\tx{ox} K (W/L)_N}} \left(1 - \frac{1}{\sqrt{K}}\right) &= I_\tx{out} R_S\\ &\Downarrow\\ I_\tx{out} &= \frac{2}{\mu_n C_\tx{ox} (W/L)_N} \cdot \frac{1}{R_S^2} \left( 1 - \frac{1}{\sqrt{K}} \right)^2 \end{aligned}\\\]

由于 the sources of $M_1$ and $M_2$ are at different voltages, 所以 $V_\tx{TH1} = V_\tx{TH2}$ 实际上会存在误差。我们可以改用 Fig. 12.2b 的电路来消除这种误差。

由于上面均忽略了 channel-length modulation，所以我们一般用长沟道来制作这部分电路，同时这也会减小 flicker noise （真不错！🥰）

但是！但是！这个电路还有一个问题！在启动时，电流为 0，所有的管子都不会打开！因此我们需要加上 $M_5$，这样就在 VDD、M3、M5、M2、GND 之间形成一条通路，就有电流啦！

Temperature-Independent References

If two quantities having opposite temperature coefficients (TCs), for example $V_1,V_2$, we can choose $\alpha_1,\alpha_2$ such that:

\[\alpha_1 \frac{\p V_1}{\p T}+ \alpha_2 \frac{\p V_2}{\p T}=0\]

so we can obtaining a reference voltage:

\[V_\tx{REF} = \alpha_1 V_1 + \alpha_2 V_2\\ \Rightarrow \frac{\p V_\tx{REF}}{\p T} = \alpha_1 \frac{\p V_1}{\p T}+ \alpha_2 \frac{\p V_2}{\p T}=0\]

Negative-TC Voltage

The forward voltage of a pn-junction diode (i.e. base-emitter voltage of bipolar transistors) exhibits a negative TC. 下面我们来求 $\p V_{BE}/ \p T$

The forward current of pn-junction is

\[\begin{aligned} I_C &= I_S [\exp(V_{BE} /V_T)-1]\\ &\approx I_S \exp(V_{BE} /V_T)\\ &= I_S \exp(qV_{BE}/kT) \end{aligned}\\ \Rightarrow V_{BE} = \frac{kT}{q}\ln (I/I_S)\quad\]

• $V_T \equiv \frac{kT}{q}$
• The saturation current $I_S \propto \mu k T n_i^2$ （参考 半导体物理器件 2.5 与 4.9）
• The mobility of minority carriers $\mu\propto \mu_0 T^m, m\approx -3/2$
• The intrinsic carrier $n_i^2 \propto T^3 \exp(-E_g/kT)$

Thus,

\[I_S = b T^{4+m} \exp \frac{-E_g}{kT}\\ b \tx{ is a prop. factor}\]

Assume that $I_C$ is held constant. Thus

\[\frac{\p V_{BE}}{\p T} = \frac{\p V_T}{\p T} \ln \frac{I_C}{I_S} - \frac{V_T}{I_S} \frac{\p I_S}{\p T}\]

其中，第一项为

\[\begin{aligned} \frac{\p V_T}{\p T} \ln \frac{I_C}{I_S} &= \frac{k}{q} \ln \left(\exp \frac{qV_{BE}}{kT} \right)\\ &= \frac{V_{BE}}{T} \end{aligned}\]

第二项为

\[\begin{aligned} \frac{V_T}{I_S} \frac{\p I_S}{\p T} &= (4+m) \frac{V_T}{T} + \frac{E_g}{kT^2} V_T\\ &= \frac{(4+m)V_T+E_g/q}{T} \end{aligned}\]

总的为：

\[\frac{\p V_{BE}}{\p T} = \frac{V_{BE}-(4+m)V_T-E_g/q}{T}\]

At $T=300\tx{K}$, $\p V_{BE}/ \p T \approx -1.5 \tx{mV/K}$

Positive-TC Voltage

If two bipolar transistors operate at unequal current densities, then the difference between their base-emitter voltages is directly proportional to the absolute temperature.

\[\begin{aligned} \Delta V_{BE} &= V_{BE1}-V_{BE2}\\ &= V_T \ln \frac{nI_0}{I_{S1}}-V_T \ln \frac{I_0}{I_{S2}}\\ &= V_T \ln n \end{aligned}\\ \Rightarrow \frac{\p \Delta V_{BE}}{\p T} = \frac{k}{q}\ln n\]

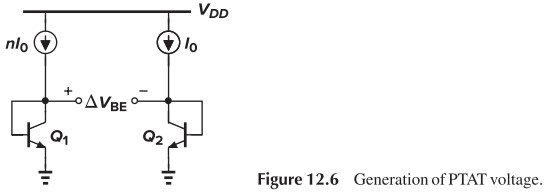
感觉这样有点取巧，本质上就是负负得正嘛……

Example 12.2 要使 TC=+1.5mV/K 以抵消 BE voltage 的 TC（$T=300K$），那么 $n$ 要取多大？

  代入 $\dfrac{k}{q} \ln n = 1.5 \tx{mV/K}$，其中 $k/q = V_T/T = 0.087 \tx{mV/K}$，得到 $\ln n \approx 17.2$，即 $n = e^{17.2} = 2.95\times 10^7$
  可见这个数很大，无法实现，所以需要修改电路。一种修改方法如下：
   修改后，右边的 $I_0$ 减小为 $\dfrac{I_0}{m}$，从而加大左右电流相对的差异，变相“增大”了 $n$。相关公式修改为：
$$ \begin{aligned} \Delta V_{BE} &= V_T \ln \frac{n I_0}{I_S} - V_T \ln \frac{I_0}{m I_S}\\ &= V_T \ln (nm) \end{aligned} $$
  但其实这还不够，后面会讨论其他方法。

Bandgap Reference

With the negative- and positive-TC voltages obtained above, we can write $V_\tx{REF} = \alpha_1 V_{BE} + \alpha_2 (V_T \ln n)$. At room temperature, $\p V_{BE}/ \p T \approx -1.5 \tx{mV/K}$, and $\p V_{T}/ \p T \approx +0.087 \tx{mV/K}$, therefore

\[\alpha_1 \times (-1.5) = \alpha_2\ln n \times (+0.087)\]

We choose $\alpha_1=1$ so that $\alpha_2\ln n = 17.2$, indicating that for zero TC

\[V_\tx{REF} \approx V_{BE}+17.2 V_T\\ \tx{一般基准电压为 1.25 V}\]

Let us now devise a circuit that adds $V_{BE}$ to $\Delta V_{BE}$

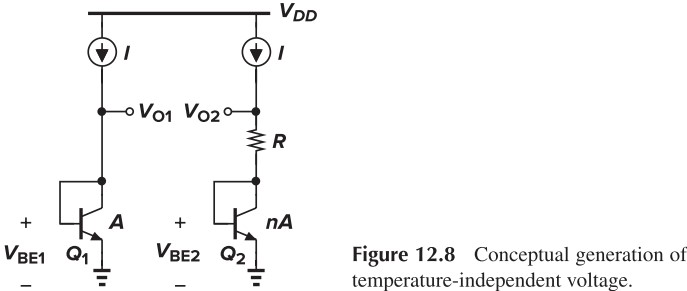
Cosider the circuit shown in Fig. 12.8, $Q_2$ 是 $n$ 个管子并联，并且我们利用某种方法使得 $V_{O1}$ 和 $V_{O2}$ 相等。那么，我们有：

\[V_{O1} = V_{O2} = RI+V_{BE2}\\ \Rightarrow RI = V_{O1}-V_{BE2} = V_{O1}-V_{O2} = V_T \ln n\\ \Rightarrow V_{O2}=V_{BE2}+R_I = V_{BE2}+V_T \ln n\]

我们可以利用运放来使 $V_{O1}$ 和 $V_{O2}$ 相等，即：

\[\begin{aligned} V_\tx{out} &= V_{BE2}+\frac{V_T \ln n}{R_3}(R_3+R_2)\\ &=V_{BE2}+(V_T \ln n)(1+\frac{R_2}{R_3}) \end{aligned}\]

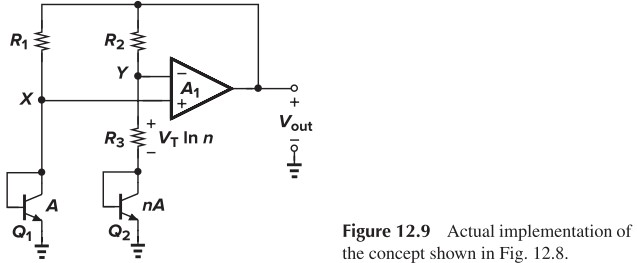
根据之前的分析，$\ln n(1+\frac{R_2}{R_3})$ 大约是 $17.2$，我们可以将 $\frac{R_2}{R_3}$ 取大一点，这样 $n$ 就不会太大。

但有时候运放会存在 Offset（失调电压），即下图中的 $V_{\tx{OS}}$，此时我们的参考电压会变为：

\[\begin{aligned} V_\tx{out} &= V_{BE2}+\frac{R_3+R_2}{R_3}(V_{BE1}-V_\tx{OS}-V_{BE2})\\ &=V_{BE2}+(1+\frac{R_2}{R_3})(V_T \ln n-V_\tx{OS}) \end{aligned}\]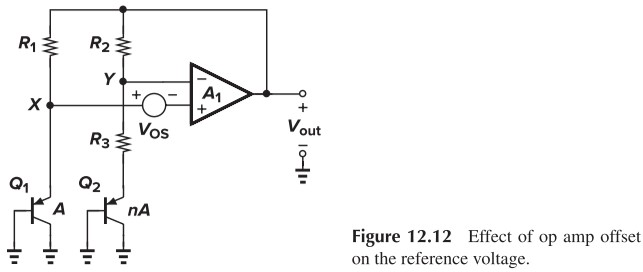

要减小 $V_\tx{OS}$ 的影响，就要增大 $V_T\ln n$，我们可以用下面的电路。注意到这个电路中有两点不同

1. $R_2=mR_1$，这导致 $\Delta V_{BE}=V_T \ln(mn)$
2. 下面串联了两个 BJT，这导致 $\Delta V_{BE}\times 2$

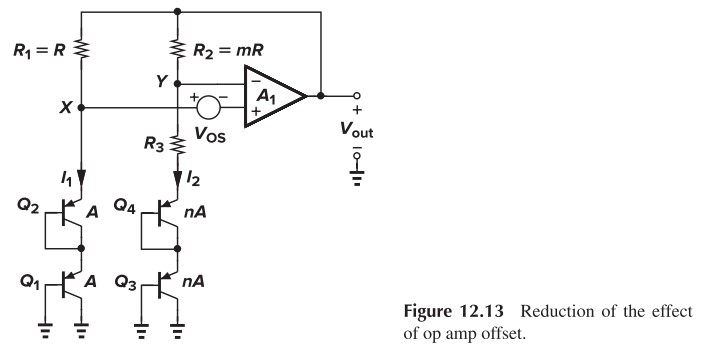
从而输出为：

\[\begin{aligned} V_\tx{out} &= V_{BE3}+V_{BE4}+\frac{R_3+R_2}{R_3}(2V_T\ln(mn))\\ &=2V_{BE}+(1+\frac{R_2}{R_3})[2V_T \ln (mn)-V_\tx{OS}] \end{aligned}\]

PTAT Current Generation