\[\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\tx}{\text} \newcommand{\L}{\mathscr{L}} \newcommand{\p}{\partial\,} \end{align*}\]

Cascode Stage

如果将两个 MOS 管按 Fig. 3.59 那样连起来，就是 cascode（表示 cascade triodes）。$M_1$ 受 $V_\tx{in}$ 调控产生电流，流经 $M_2$ 后产生 $V_\tx{out}$

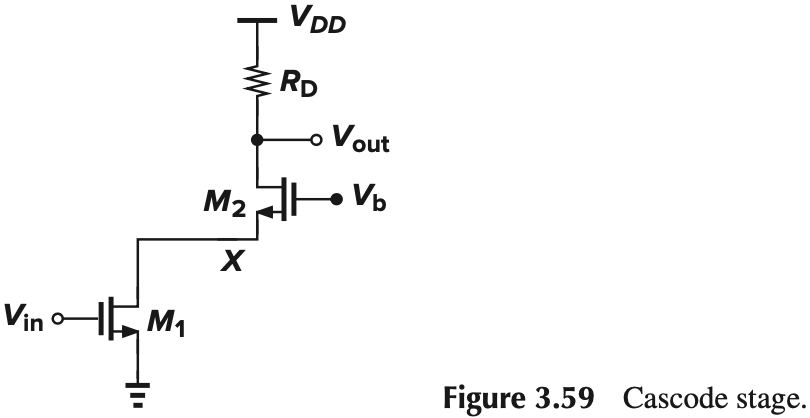
我们可以利用 CS stage 和 CG stage 的公式简略分析一下。假设两管都饱和，并且 $\lambda=\gamma=0$，那么：

• 对 $M_1$ 来说，负载是从 $M_2$ 源端看进去的电阻，故 $A_{v1}=-\dfrac{g_{m1}}{g_{m2}}$
• 对 $M_2$ 来说，$A_{v2}=g_{m1}R_D$

从而总的增益为：$A_v = A_{v1}A_{v2}=-g_{m1}R_D$，这个结果和 CS stage 是一样的（Fig. 3.60b）

注意到如果 $M_1,M_2$ 上的电流相等，那么它们的偏置必须满足一定的要求，并且输出幅度也会受偏置影响，具体分析如下：

1. 两管工作在饱和区：
   • $V_\tx{in}>V_\tx{TH1}$ 且 $V_\tx{in}-V_\tx{TH1} \leq V_X$
   • $V_b-V_X>V_\tx{TH2}$ 且 $V_b-V_\tx{TH2} \leq V_\tx{out}$
2. 电压间满足一定关系：
   • $V_X=V_b-V_{GS2}$
   • $V_\tx{in}=V_{GS1}$

从而：

\[\begin{aligned} V_\tx{out} &\geq V_\tx{in} - V_\tx{TH1}+V_{GS2}-V_\tx{TH2}\\ &=(V_{GS1}-V_\tx{TH1})+(V_{GS2}-V_\tx{TH2}) \end{aligned}\]

说明输出电压的下限是两管 overdrive voltage 之和。

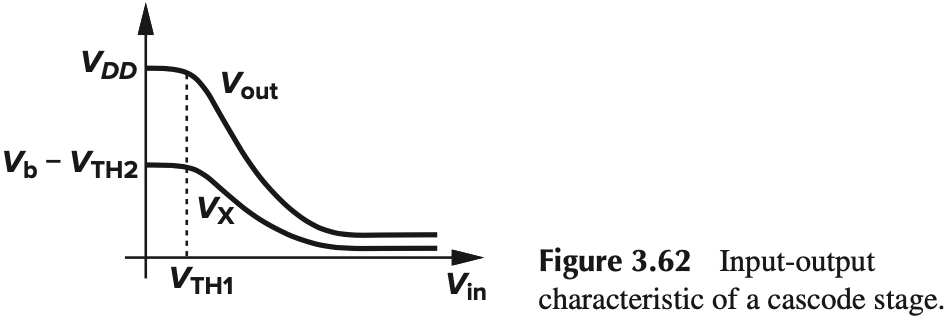
以上只是饱和区的情况，完整的 large-sianl behavior 如下（分析过程略）：

---

小信号模型如下：

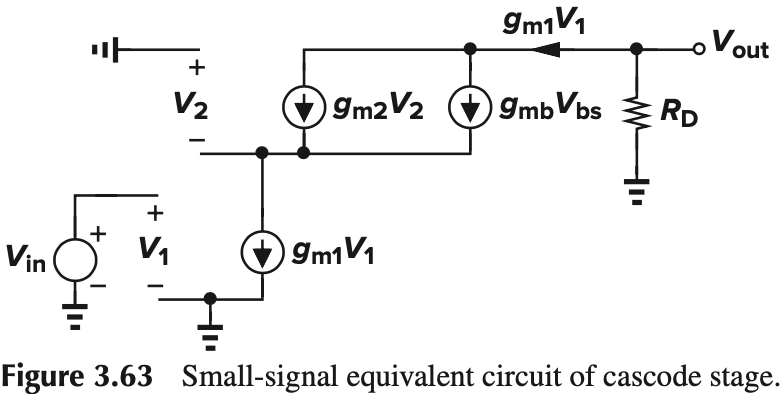
注意到输出端的电流只能是 $g_{m1}V_1$，从而 $A_v = -g_{m1}R_D$，与 $M_2$ 无关。但这是忽略了 $M_1$ 的 $r_{O1}$ 的结果（$g_{mb1}$ 忽不忽略都一样），如果考虑上沟道长度调制，结果会不同。如图 Fig. 3.64，$r_O$ 会起到一个分流的作用。因此：

\[I_{D2} = g_{m1}V_\tx{in} \frac{g_{m2}+g_{mb2}}{\frac{1}{r_{O1}}+(g_{m2}+g_{mb2})}\]

$(g_{m2}+g_{mb2})$ 为从 $M_2$ 源端看进去的电导。从而增益为：

\[A_v = g_{m1} \frac{g_{m2}+g_{mb2}}{\frac{1}{r_{O1}}+(g_{m2}+g_{mb2})} R_D\]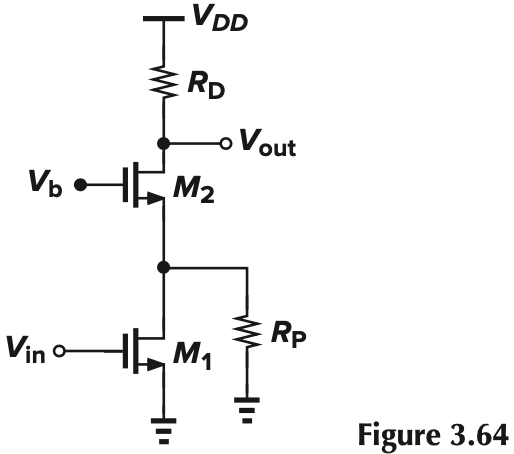

---

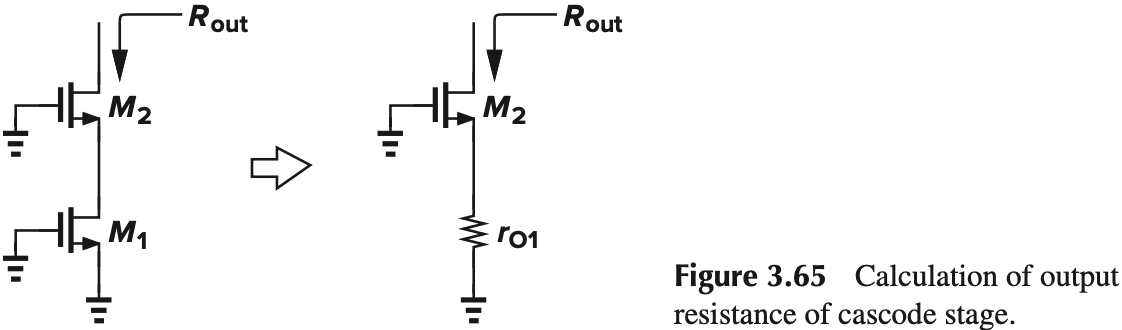
下面来计算输出电阻。注意到 $M_1$ 可以当作是 degeneration resister $r_{O1}$，从而输出电阻与前面（CS Stage with Source Degeneration）的一样：

\[\begin{aligned} R_\tx{out} &= [1+(g_{m2}+g_{mb2})r_{O2}]r_{O1}+r_{O2}\\ &\approx (g_{m2}+g_{mb2})r_{O2}r_{O1} \end{aligned}\]

注意到输出电阻可以看作是 $r_{O1}$ 增大了 $(g_{m2}+g_{mb2})r_{O2}$ 倍，如果级联多级，我们可以得到很高的输出电阻（当然，trade off 是电压摆幅减小）

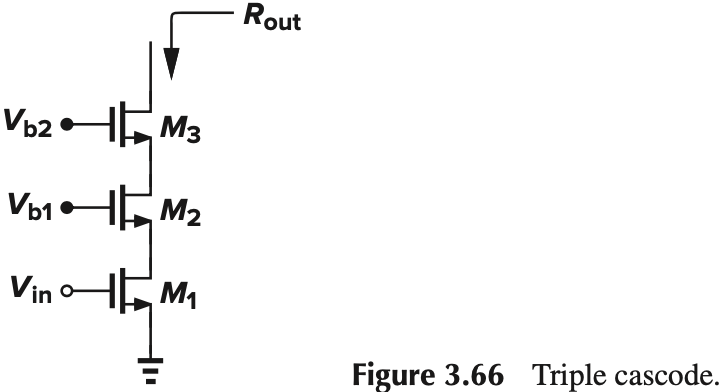
输出阻抗大有什么用呢？这里我们要介绍 Shielding Property，由于输出阻抗大，当输出电压变化时，反应到源端的电压变化就会小。我们用下面这里例子来说明。

$V_X$ is higher than $V_Y$ by $\Delta V$. Calculate the resulting difference between $I_{D1}$ and $I_{D2}$ if $λ≠0$.

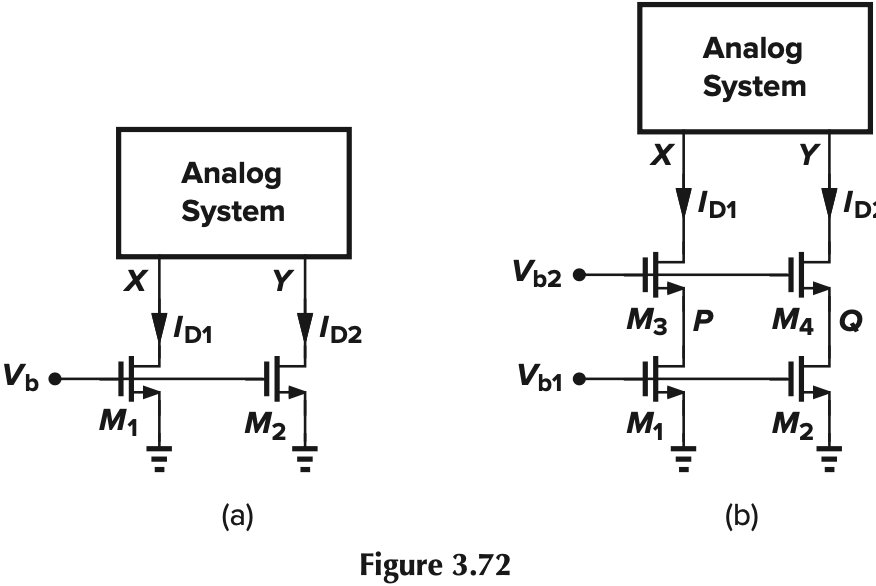
(a) We have
$$ \begin{aligned} I_{D1}-I_{D2} &= \frac{1}{2} \mu_n C_\tx{ox} \frac{W}{L} (V_b-V_\tx{TH})^2 (\lambda V_{DS1}-\lambda V_{DS2})\\ &=\frac{1}{2} \mu_n C_\tx{ox} \frac{W}{L} (V_b - V_\tx{TH})^2 (\lambda \Delta V) \end{aligned} $$
(b) Cascode 起到分压的作用
$$ \begin{aligned} \Delta V_{PQ} &= \Delta V \frac{r_{O1}}{[1+(g_{m3}+g_{mb3})r_{O3}]r_{O1}+r_{O3}}\\ &\approx \frac{\Delta V}{(g_{m3}+g_{mb3})r_{O3}} \end{aligned} $$
Thus,
$$ I_{D1}-I_{D2}=\frac{1}{2} \mu_n C_\tx{ox} \frac{W}{L} (V_b - V_\tx{TH})^2 \frac{\lambda \Delta V}{(g_{m3}+g_{mb3})r_{O3}} $$
In other words, cascoding reduces the mismatch between $I_{D1}$ and $I_{D2}$ by a factor of $(g_{m3} + g_{mb3})r_{O3}$.（个人觉得这就是简单的加大电阻来减小电流变化🧐）

The shielding property of cascodes diminishes if the cascode device enters the triode region. because
$$ I_{D2}=\frac{1}{2}\mu_n C_\tx{ox} \left(\frac{W}{L}\right)_2\left[ 2(V_{b2}-V_P-V_\tx{TH2})(V_X-V_P)-(V_X-V_P)^2 \right] $$
As $V_X$ decreases, $V_P$ also drops, so that $I_{D2}$ remains constant.

由于这个特性十分重要，我上网搜了些资料，然后在知乎上发现了一篇很好的文章 模拟电路基础之运放的增益计算（三）cascode，里面提到一种很有趣的理解方法，在此记录一下。

我们考虑共栅管的小信号模型。由于 G 是接恒压源，可看作地，从而 $V_{GS}=-V_S$，所以图中电流源方向是反的。

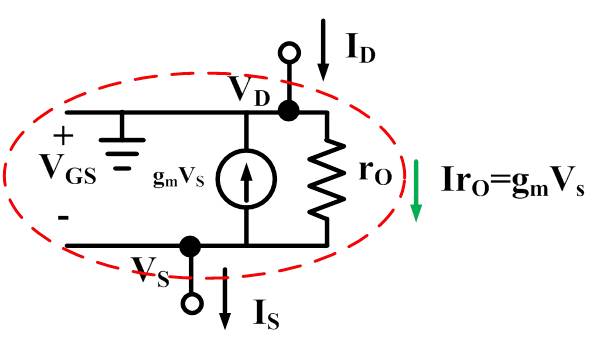
根据 KCL，如果我们把整个管看作一个结点，则 $I_S=I_D$（此处指直流大信号）。所以，这个 $g_mV_S$ 的电流，其实是“自生自灭”的！无路可退的这个 mos 人，只好把一肚子的怨气深埋在心底，自己消化掉。

所以，流过 $r_O$ 的电流，就是反方向的 $g_mV_s$，这样看来，这个 mos 上的压降 $V_{DS}$就等于 $r_og_mV_S$

因此，当我们计算 $V_D$ 的电压时，有：

\[\begin{aligned} V_D&=V_S+V_{DS}\\ &=V_S+r_Og_mV_S\\ &=(1+r_Og_m)V_S \end{aligned}\]

因为我们的 $g_mr_O$ 一般能够达到一百以上，所以 $V_D$ 就大约等于 $g_mr_OV_S$。因此我们可以得到一个 Golden Rule：从 s 看到 d，电压被放大了 $g_mr_O$ 倍；从 d 看到 s，电压被缩小了 $g_mr_O$ 倍。（前提：g 接恒压源且 mos 工作在饱和区）

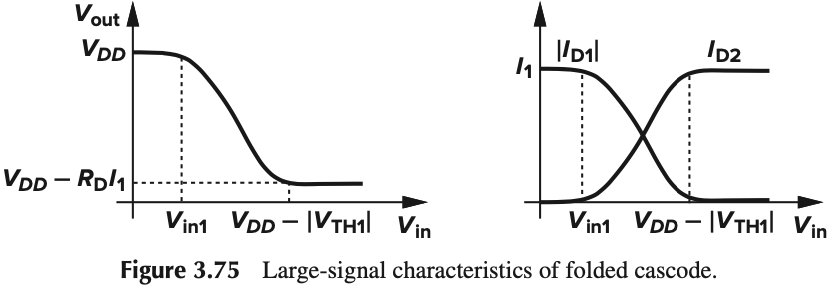
Folded Cascode

之前两个都是 NMOS，现在是一个 PMOS 给 NMOS 提供电流。

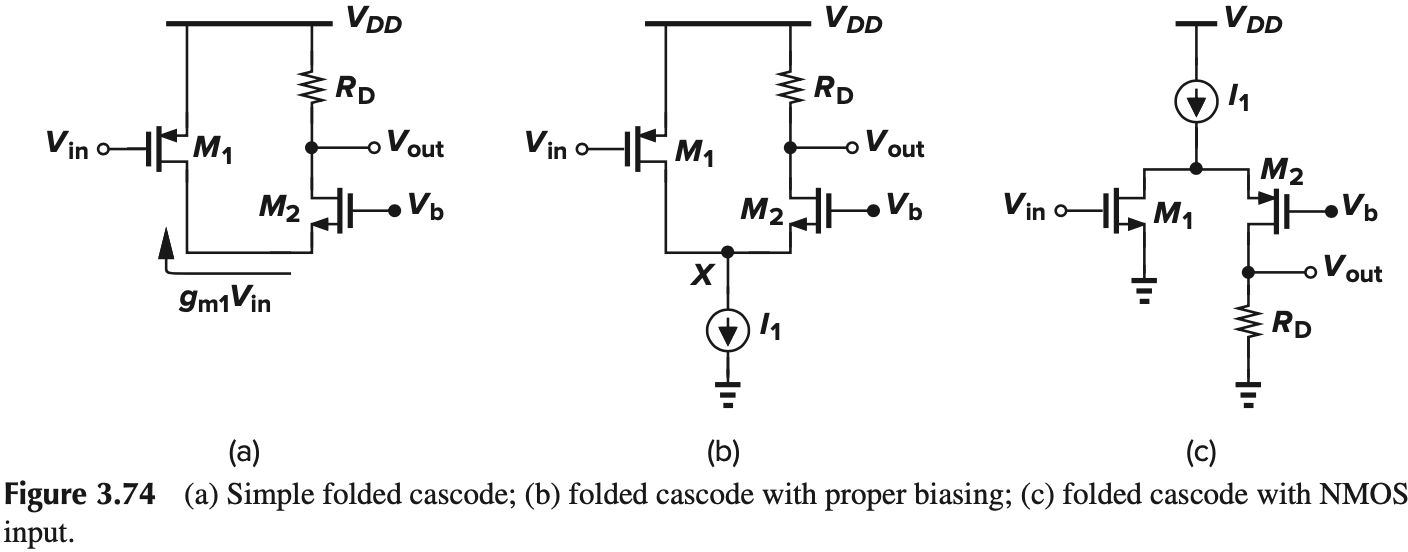
$I_1$ 用于提供直流偏置，显然 $\vert I_{D1}\vert+I_{D2}=I_1$，如果 $I_{D1}$ 变小，就会使得 $I_{D2}$ 变大，从而改变 $V_\tx{out}$

大信号分析如下：

• $V_\tx{in}>V_{DD}-\vert V_\tx{TH1} \vert$，$M_1$ is off and $M_2$ carries all of $I_1$. yielding $V_\tx{out}=V_{DD}-I_1R_D$
• $V_\tx{in}<V_{DD}-\vert V_\tx{TH1} \vert$, $M_1$ turns on in saturation, giving

\[I_{D2}=I_1-\frac{1}{2}\mu_p C_\tx{ox} \left( \frac{W}{L} \right)_1 (V_{DD}-V_\tx{in}-\vert V_\tx{TH1} \vert)^2\]

• $I_{D2}$ decrease further as $V_\tx{in}$ drops. If $I_{D2}=0$, $V_\tx{out}=V_{DD}$. The $V_\tx{in}$ at this point is denoted as $V_\tx{in1}$

\[\frac{1}{2}\mu_p C_\tx{ox} \left( \frac{W}{L} \right)_1 (V_{DD}-V_\tx{in1}-\vert V_\tx{TH1} \vert)^2=I_1\]

Thus,

\[V_\tx{in1} = V_{DD}-\sqrt{\frac{2I_1}{\mu_p C_\tx{ox}(W/L)1}} - \vert V_\tx{TH1} \vert\]