单极放大器作业

\[\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\tx}{\text} \newcommand{\L}{\mathscr{L}} \newcommand{\p}{\partial\,} \end{align*}\]

关于模型的选择（是否要考虑 $r_O,g_{mb}$）：

• 在计算偏置时，不需要考虑二级效应（即 $r_O,g_{mb}$）
• 题目没有说，则默认要考虑二级效应，但如果题目太复杂，可以只考虑某些地方的二级效应，比如：
  1. 如果器件的漏极连接一个高阻抗（如另一个器件的源极），那么要考虑 $r_O$

关于公式的记忆：

• 只需要记考虑 $r_O,g_{mb}$ 的公式，其余公式可推出来
• 那个，共栅和其他几个公式不太一样，有人有好方法记吗？😫

求源极负反馈的输出阻抗：

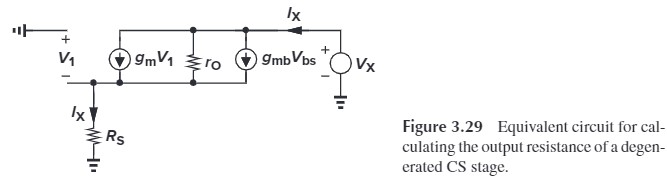
根据小信号模型，我们有：
$$ V_X = (I_X-g_mV_1-g_{mb}V_{bs})r_O+I_XR_S\\ \tx{where } V_1=V_{bs}=-I_XR_S\\ \Rightarrow V_X=[I_X+(g_m+g_{mb})R_SI_X]r_O+I_XR_S $$
可以算出：
$$ \begin{aligned} R_\tx{out} &= \frac{V_X}{I_X}\\ &= [1+(g_m+g_{mb})R_S]r_O+R_S\\ &= [1+(g_m+g_{mb})r_O]R_S+r_O\\ &= R_S+r_O+(g_m+g_{mb})r_OR_S \end{aligned} $$

求下图的输出阻抗：

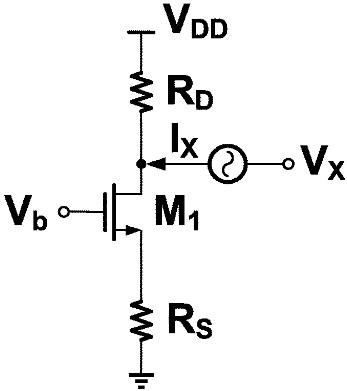
只需要将上面源极负反馈的输出阻抗并联上 $R_D$ 即可：$R_\tx{out}=\{[1+(g_m+g_{mb})R_S]r_O+R_S\} \Vert R_D$

3.2 In the circuit of Fig. 3.18, assume that $(W/L)_1=50/0.5$, $(W/L)_2=50/2$, and $I_{D1}=I_{D2}=0.5 \tx{mA}$ when both devices are in saturation. Recall that $λ∝1/L$.
(a) Calculate the small-signal voltage gain.
(b) Calculate the maximum output voltage swing while both devices are saturated.

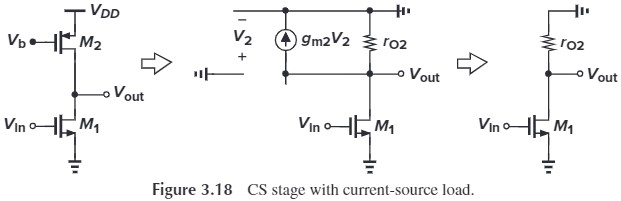
Solution:
(a) $A_v = -g_{m1}(r_{O1}\Vert r_{O2})$ where $g_m=\sqrt{2 \mu_n C_\tx{ox} \frac{W}{L} I_D}$ and $r_{O}\approx \dfrac{1}{\lambda I_D}$, therefore
$$ \begin{aligned} g_{m1}&=\sqrt{2\times 1.34225\times 10^{-4} \times \frac{3.9}{9\times 10^{-9}}\times 50/0.5 \times 0.5 \times10^{-3}}\\ &=3.664\times 10^{-3}\\ r_{O1}&=\frac{1}{0.1\times 0.5 \times 10^{-3}}=20 {\rm k\Omega}\\ r_{O2}&=\frac{1}{0.2\times 0.5 \times 10^{-3}}=10 {\rm k\Omega}\\ A_v &= 3.664 \times 10^{-3} \times \frac{20 \times 10^3\times 10\times 10^3}{20 \times 10^3+ 10\times 10^3}\\ &=24.43 \end{aligned} $$
(b) $M_1,M_2$ are in saturation, therefore
$$ V_\tx{in}-V_\tx{out}\leq V_\tx{TH1}\\ V_\tx{b}-V_\tx{out}\geq V_\tx{TH2}\\ \Rightarrow V_\tx{in}-V_\tx{TH1}\leq V_\tx{out}\leq V_\tx{b}-V_\tx{TH2} $$
Assuming that $M_1$ is on the edge of the triode region, we have
$$ \begin{aligned} I_D &= \frac{1}{2} \mu_n C_\tx{ox} (\frac{W}{L})_1(V_\tx{in}-V_\tx{TH1})^2(1+\lambda_n V_\tx{out})\\ &\leq \frac{1}{2} \mu_n C_\tx{ox} (\frac{W}{L})_1 V_\tx{out}^2(1+\lambda_n V_\tx{out}) \end{aligned}\\ $$
Solve $$ 0.5\times 10^{-3}=\frac{1}{2}\times 1.34225 \times 10^{-4}\times 50/0.5\times V_\tx{out}^2(1+0.1 V_\tx{out})\\ $$ and we have
$$ V_\tx{out,min}=0.2693 \tx{ V} $$
Assuming that $M_2$ is on the edge of the triode region, we have
$$ \begin{aligned} I_D &= \frac{1}{2} \mu_p C_\tx{ox} (\frac{W}{L})_1(V_{SG2}-\vert V_\tx{TH2} \vert)^2(1+\lambda_n V_{SD2})\\ &\leq\frac{1}{2} \mu_p C_\tx{ox} (\frac{W}{L})_1 V_{SD2}^2(1+\lambda_n V_{SD2}) \end{aligned} $$
Solve $$ 0.5\times 10^{-3}=\frac{1}{2}\times 1.3835 \times 10^{-4}\times 50/2\times V_\tx{out}^2(1+0.2 V_\tx{out})\\ $$ and we have
$$ V_\tx{SD,min}=0.9967 \tx{ V}\\ V_\tx{out,max}=V_{DD}-V_\tx{SD,min}=2.003 \tx{ V} $$

3.17 Sketch $V_\tx{out}$ versus $V _\tx{in}$ for the circuits of Fig. 3.80 as $V_\tx{in}$ varies from 0 to $V_\tx{DD}$. Identify important transition points.

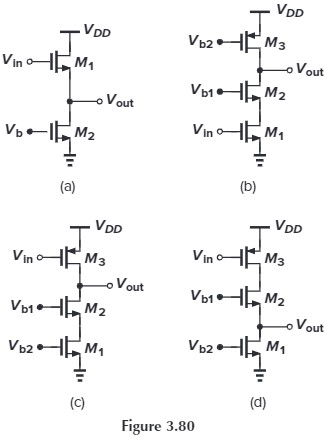
(a)

(b)

(c)

(d)（第二条式子多了个平方）

  我利用 Cadence 对 (c)(d) 电路进行了仿真，仿真结果如下（注意粉色的曲线是电流⚡）

  对(c)(d)电路的详细分析：我们设 (c) 中输出为 $V_X$，(d) 中输出为 $V_Y$
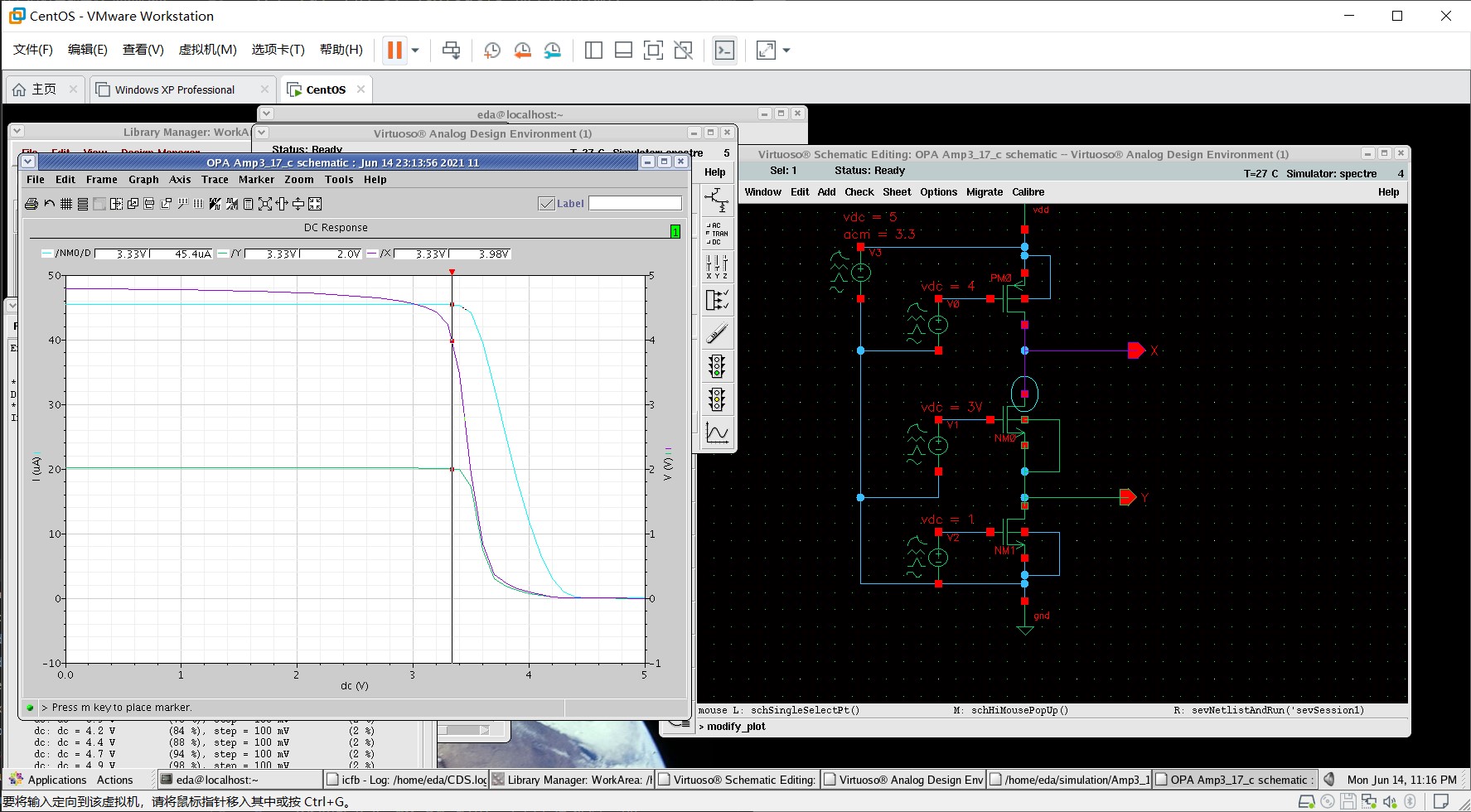
  不妨先考虑三个管子均饱和的情况。此时，若减小 $V_\tx{in}$，根据 $I_{D3}=\frac{1}{2}K_p(W/L) (V_{GS3}-V_\tx{TH3})^2$，$I_D$ 会变大，此时考虑 $M_1$，由于 $V_{GS1}$ 是固定的，所以如果不考虑沟道长度调制效应，$I_{D1}$ 不会变，这就产生了矛盾。故根据 $I_{D1}=\frac{1}{2}K_n(W/L) (V_{GS1}-V_\tx{TH1})^2(1+\lambda V_{DS1})$，$V_{DS1}$ 应该变大，即 $V_Y$ 应该变大，并且 $V_Y$ 与 $V_\tx{in}$ 之间应该为 2 次关系（开口向上）。$M_2$ 的情况与 $M_1$ 类似，但由于 $V_Y$ 上升导致 $V_{GS2}$ 变小，所以要使 $I_{D2}$ 同等变大，那么 $V_{DS2}$ 增大的幅度也应该更大（对应图中两线分离的部分）。
  然后考虑左边的情况，随着 $V_\tx{in}$ 减小且 $V_X$ 增大，$M_3$ 会进入 Triode，这么一来，$I_{D3}=K_p (W/L)[(V_{GS3}-V_\tx{TH})V_{DS3}-\frac{1}{2}V_{DS3}^2]$，注意到 $V_{GS3}$ 变大的同时 $V_X$ 会变大（$V_{DS3}$ 变小），这两者的作用会相互抵消，导致 $I_{D3}$ 几乎不变，从而 $V_{DS2},V_{DS1}$ 也几乎不变（对应图中下面的曲线平的那一段）
  （关于上一段的进一步解释。首先，既然 $I_D$ 不变，那么 $M_1,M_2$ 三端的电压也应该不变，否则电流就会变，但我们注意到图像中 $V_X$ 却会变大，这显然是矛盾的，唯一的解释就是此时不需要管 $M_2$ 的沟道长度调制效应了。另一个矛盾点是，我们易知：$\dfrac{\p I_{D3}}{\p V_{GS3}}=V_{DS}$，但图像中 $I_{D3}$ 并不随 $V_{GS3}$ 变化，所以这应该是 0，但显然 $V_{DS}\neq 0$😱，这点我实在解释不了……）
  

如何分析？

1. 先分析输入管的初始状态（要么是 Triode 要么是 Off），并分析此时有无 $I_D$
2. 然后根据 $I_D$ 相同，来得到其他管的状态
3. 然后改变输入
4. 由于各管的状态不会突变（Off到Sat到Tri，或反过来），故可以给

3.21 Assuming all MOSFETs are in saturation, calculate the small-signal voltage gain of each circuit in Fig. 3.84($λ \neq 0,γ=0$).

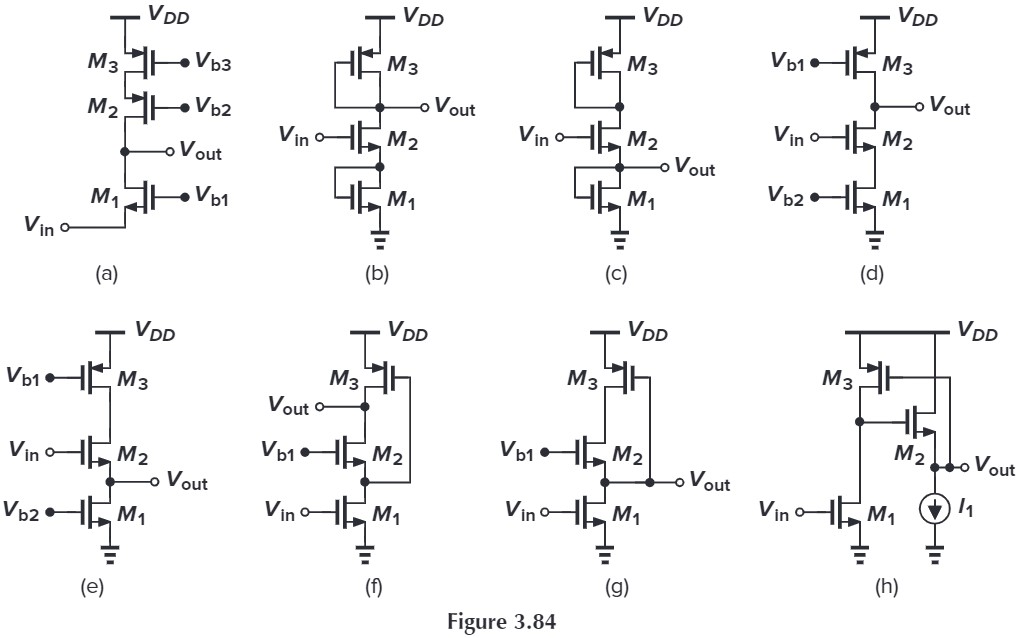
因为题目说 $\lambda=0,\gamma=0$，也就是忽略所有的体效应和沟道长度调制效应，所以 $g_{mb}=0,r_O=\infty$，所以有些题目是无解的。答案上没有忽略 $r_{O}$，那我就当 $\gamma\neq 0$ 来做。

(a)

(b)

(c)

(d) $M_1,M_3$ 可看作 $r_{O1},r_{O3}$，根据前面的公式：
$$ \begin{aligned} A_v &=-G_m(R_\tx{out}\Vert R_D)\\ &= - \frac{g_mr_O}{R_S+r_O+g_mR_Sr_O}\cdot \frac{1}{\frac{1}{R_D}+\frac{1}{[R_S+r_O+g_mR_Sr_O]}} \end{aligned} $$
令 $R_S=r_{O1}$，$r_O=r_{O2}$，$R_D=r_{O3}$ 可得：
$$ \begin{aligned} A_v&=-\frac{g_{m2}r_{O2}}{r_{O1}+r_{O2}+g_{m2}r_{O2}r_{O1}}\cdot \frac{1}{\frac{1}{r_{O3}}+\frac{1}{[r_{O1}+r_{O2}+g_{m2}r_{O2}r_{O1}]}}\\ &=\frac{g_{m2}r_{O2}r_{O3}}{r_{O1}+r_{O2}+r_{O3}+g_{m2}r_{O2}r_{O1}} \end{aligned} $$

(e)
$$ \begin{aligned} R_\tx{out} &= \frac{r_{O3}+r_{O2}}{1+g_m r_{O2}}\\ A_v &= \frac{V_\tx{out}}{V_\tx{in}}=\frac{r_{O1}}{r_{O1}+\frac{r_{O3}+r_{O2}}{1+g_{m2}r_{O2}}} \end{aligned} $$

(f)

(g)

(h)
在输入支路上，有：
$$ -(\frac{V_X}{r_{O3}}+g_{m3}V_\tx{out})=g_{m1}V_\tx{in}+\frac{V_X}{r_{O1}} $$
在输出支路上，有：
$$ -\frac{V_\tx{out}}{r_{O2}}+g_{m2}(V_X-V_\tx{out})=0\\ \Rightarrow V_X=\frac{\frac{1}{r_{O2}}+g_{m2}}{g_{m2}}V_\tx{out} $$
将 $V_X$ 代入输入支路表达式，有：
$$ -(\frac{1}{r_{O3}}\frac{\frac{1}{r_{O2}}+g_{m2}}{g_{m2}}V_\tx{out}+g_{m3}V_\tx{out})=g_{m1}V_\tx{in}+\frac{1}{r_{O1}}\frac{\frac{1}{r_{O2}}+g_{m2}}{g_{m2}}V_\tx{out}\\ $$
解得：
$$ A_v = \frac{V_\tx{out}}{V_\tx{in}}=-\frac{g_{m1}}{g_{m3}+(\frac{1}{r_{O3}}+\frac{1}{r_{O1}})\frac{\frac{1}{r_{O2}}+g_{m2}}{g_{m2}}} $$