\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}}
\newcommand{\bd}{\boldsymbol}
\newcommand{\tx}{\text}
\newcommand{\L}{\mathscr{L}}
\newcommand{\p}{\partial\,}
\end{align*}\]
%20diode-connected%20and%20(b)%20current-source%20loads.jpg "Figure 4.37 Differential pair with (a) diode-connected and (b) current-source loads")
- Describe advantages and drawbacks of differential signals comparing with
single-ended signal.
- Advantages:
- Higher immunity to environmental noise 更高的环境噪声抑制
- Reject supply noise 更高的电源噪声抑制
- Increase output swing from $V_{DD}-(V_{GS}-V_\tx{TH})$ to $2[V_{DD}-(V_{GS}-V_\tx{TH})]$ 更大的摆幅
- Higher linearity 更高的线性度
- Drawbacks:
- occupy twice area 占两倍面积
- Advantages:
- What is the problem of simple differential circuit? How to solve this problem?
- 问题：如果输入共模电平 Vin,CM 太低,输出会被截断。
- 解决方案：使用差分对电路，并引入电流源$I_{SS}$
- 为什么这样能解决？因为引入 $I_{SS}$ 后，$V_S$ 会随着输入共模电平变化，从而 $V_{GS}$ 始终是一个合适的值。
- If all symmetry（对称的）, is the small signal gain（小信号增益） of differential pair __ than that of the common-source single stage?
- 要比较这两者，关键是比较 $I_D$
- $I_D$ 相同，则两者相同；$I_{SS}$ 相同，由于差分对的 $I_D=I_{SS}/2$，故比单端的要小。
- If there is a small mismatch between $M_1$ and $M_2$, how do the parameters of the transistors affect the common mode rejection ratio (CMRR) of a differential pair?
- $\tx{CMRR}\approx\frac{g_m}{\Delta g_m}(1+2g_m R_{SS})$
- 如果 $g_{m1}$ 与 $g_{m2}$ 不匹配，就会导致 CMRR 减小。
- Write the gain ($A_v$) expression of a differential pair with current-source load (Fig.2). How to increase its gain?
- $A_v = -g_{mN}(r_{ON}\Vert r_{OP})$
- increase $g_{mN}$ (i.e. $\frac{W}{L}$) or $r_{ON}$ or $r_{OP}$ by increasing L1~L4
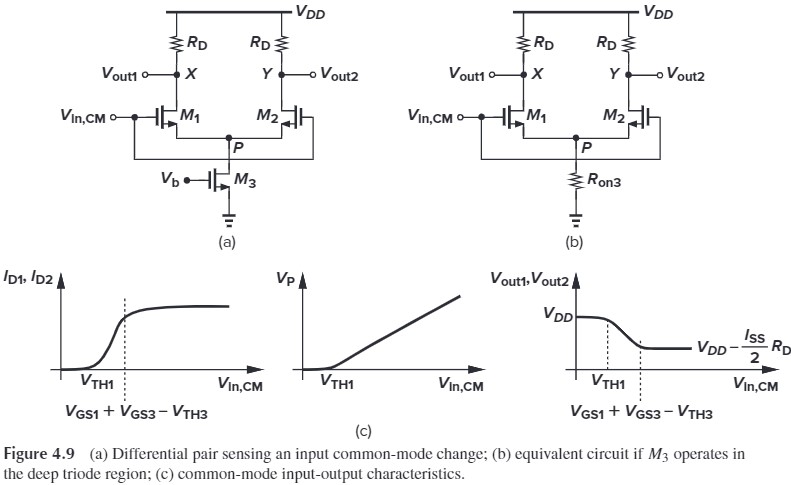
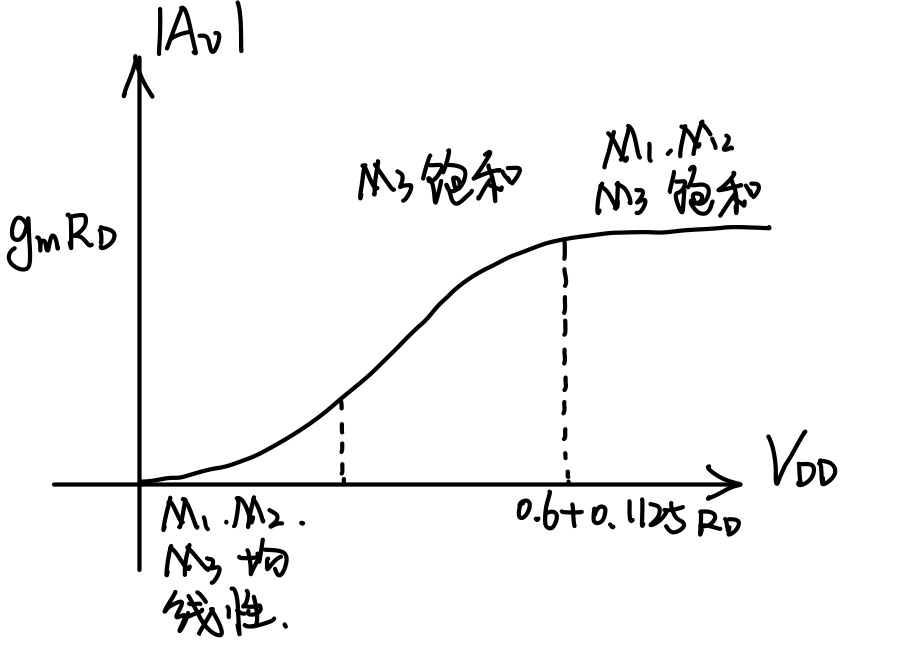
4.2 Sketch the small-signal differential voltage gain of the circuit shown in Fig. 4.9(a) if $V_{DD}$ varies from 0 to 3V. Assume that $(W/L){1−3}=50/0.5$,$V\tx{in,CM}=1.3\tx{ V}$,and $V_b=1 \tx{ V}$.
- $V_{DD}=0$，$M_1,M_2,M_3$ 处于线性区
- 随着 $V_{DD}$ 增大，$M_3$ 进入饱和，此时 $I_{SS} = \frac{1}{2}\mu_n C_\tx{ox} (\frac{W}{L})(V_{GS3}-V_\tx{TH})^2=0.225 \tx{ mA}$
- 随着 $V_{DD}$ 进一步增大，$M_1,M_2$ 进入饱和区，此时有 $V_\tx{in,CM}=V_{DD}-R_DI_{SS}/2+V_\tx{TH}$，算得 $V_{DD}=0.6+0.1125 R_D \tx{ mV}$
则增益草图为：
4.13 In Problem 4.11, suppose $W_3=10 \tx{ μm}$, but $W_4=11 \tx{ μm}$. Calculate the CMRR.
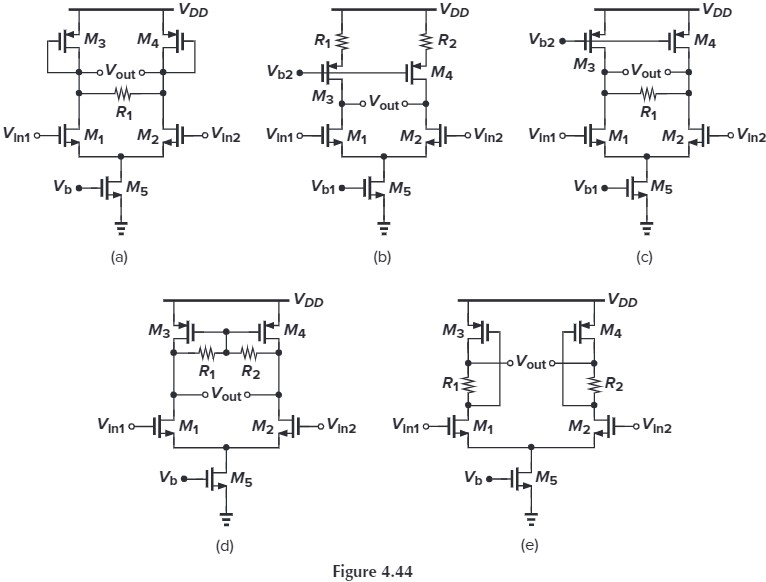
4.18 Assuming that all the transistors in the circuits of Figs. 4.44 and 4.45 are saturated and $λ\neq 0$, calculate the small-signal differential voltage gain of each circuit.
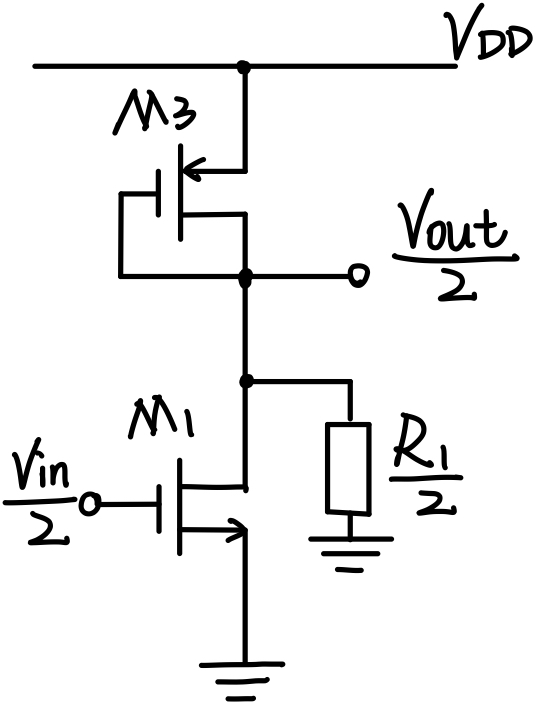
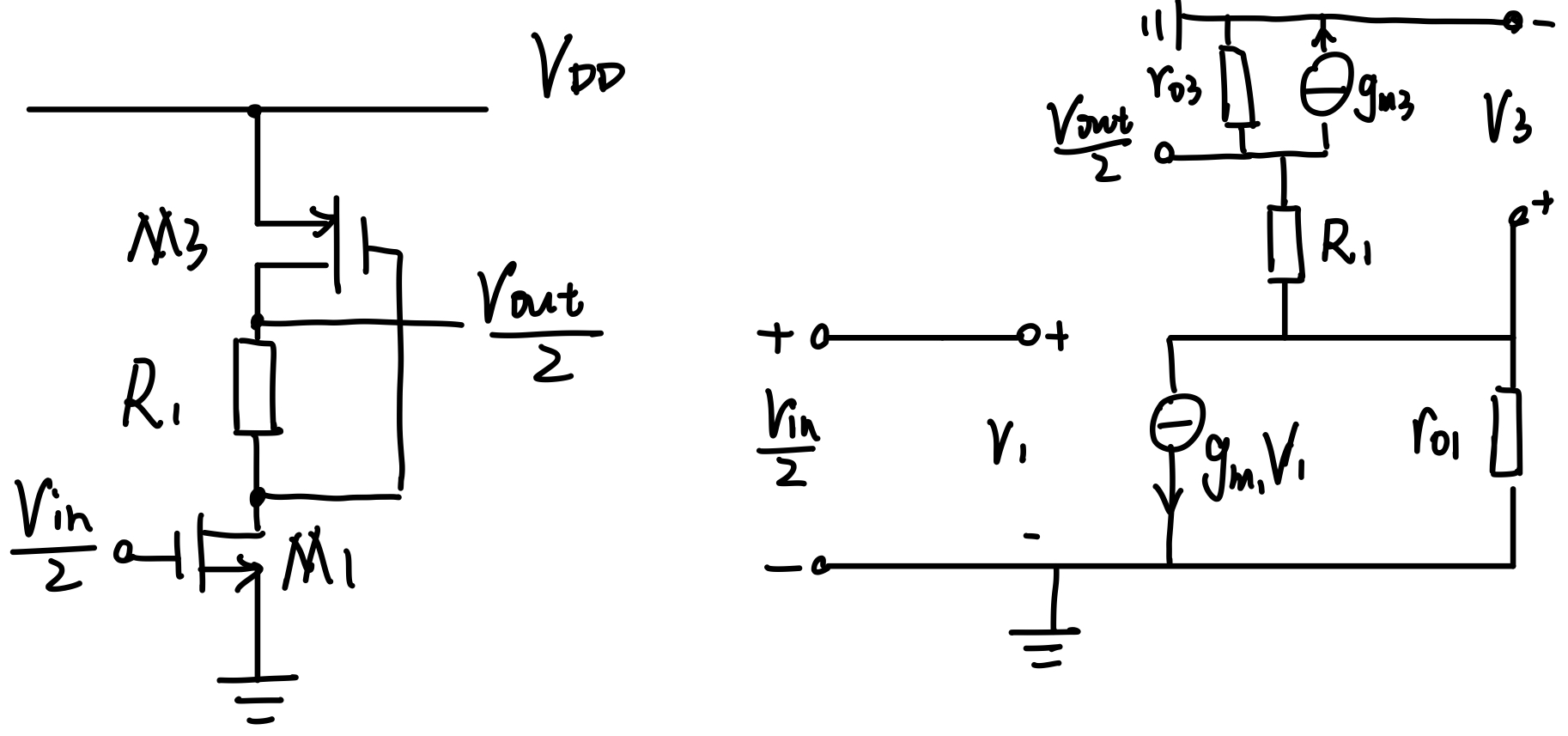
For Fig. 4.44(a), $R_1$ 中间可看作是 0 电位（差分信号的中间），故半边电路为：
For Fig.4.44(e)，半边电路为：
对小信号模型进行分析（$V_X$ 为 $R_1$ 下端的电压）：
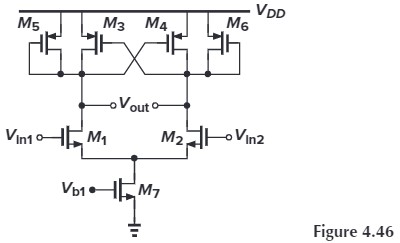
\[-\frac{V_X}{r_{O1}}-\frac{g_{m1}V_\tx{in}}{2} = \frac{V_X - \frac{V_\tx{out}}{2}}{R_1} = \frac{V_\tx{out}}{2r_{O3}}+g_{m3} V_X\\ 由后一个等号得：V_X = \frac{(r_{O3}+R_1)V_\tx{out}}{2r_{O3}(1-R_1g_{m3})}\\ 代入原式有：\\ V_\tx{out} (\frac{R_1+r_{O1}}{R_1 r_{O1}}\cdot \frac{r_{O3}+R_1}{r_{O3}(1-R_1g_{m3})}-\frac{1}{R})=-g_{m1} V_\tx{in}\\ 从而：\\ A_v = \frac{V_\tx{out}}{V_\tx{in}} = - \frac{g_{m1}r_{O1}r_{O3}(1-R_1 g_{m3})}{R_1+r_{O1}+r_{O3}+g_{m3}r_{O1}r_{O3}}\]4.19. Consider the circuit shown in Fig. 4.46.
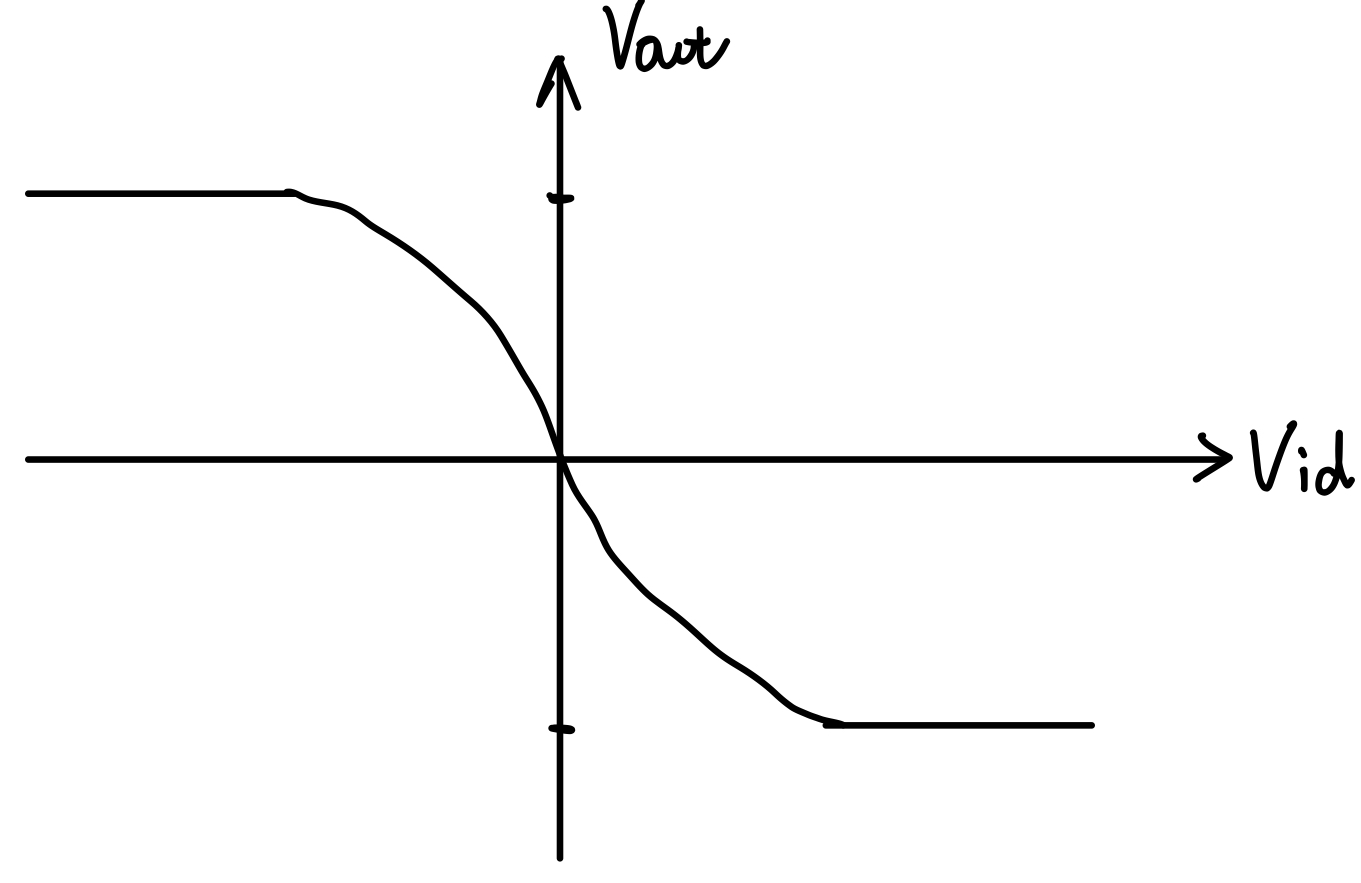
- Sketch $V_\tx{out}$ as $V_\tx{in1}$ and $V_\tx{in2}$ vary differentially from zero to $V_{DD}$.
- If $λ=0$, obtain an expression for the voltage gain. What is the voltage gain if $W_{3,4}=0.8W_{5,6}$
(a)
(b) 这题难在 $M_3,M_4$ 组成的交叉结构，我们先计算该结构的输入阻抗：
\[I_X = g_{m3} V_2\\ I_X = -g_{m4} V_1\\ \Rightarrow 2I_X = -g_{m3,4}(V_1-V_2)=-g_{m3,4} V_X\\ \Rightarrow \frac{V_X}{I_X} = -\frac{2}{g_{m3,4}}\]从而我们可以画出半边电路并写出增益：
\[\begin{aligned} A_v &= -g_{m1} (\frac{1}{g_{m5}}\Vert \frac{-1}{g_{m3}})\\ &= \frac{g_{m1}}{g_{m5}-g_{m3}} \end{aligned}\\ \tx{要求 } g_{m5}>g_{m3}\]又因为：
\[g_m = \mu_p C_\tx{ox} \frac{W}{L} (V_{GS}-V_\tx{TH})\\ \Rightarrow \frac{g_{m3,4}}{g_{m5,6}} = \frac{(W/L)_{3,4}}{(W/L)_{5,6}} = 0.8\]故最终得到：
\[A_v = -\frac{g_{m1}}{g_{m5}-0.5g_{m5}} = -\frac{5 g_{m1}}{g_{m5}}\]