\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}}
\newcommand{\bd}{\boldsymbol}
\newcommand{\tx}{\text}
\newcommand{\p}{\partial\,}
\end{align*}\]
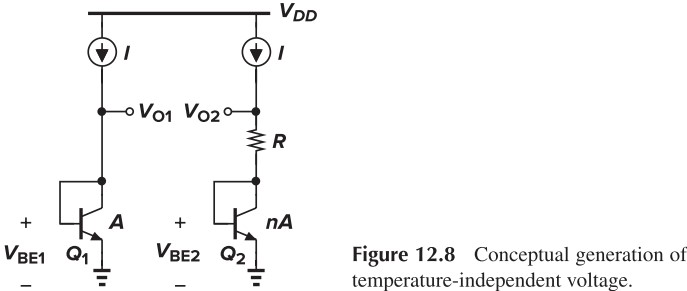
- Explain briefly why the circuit in Fig. 11.8 can be temperature-independent.

Suppose we somehow force $V_{O1}=V_{O2}$, then $IR = V_{BE1}-V_{BE2} = V_T \ln n$. Thus, $V_{O2}=V_{BE2}+V_T\ln n$. Because $V_{BE2}$ has a negative TC and $V_T \ln n$ has a positive TC, $V_{O2}$ might have a zero TC.
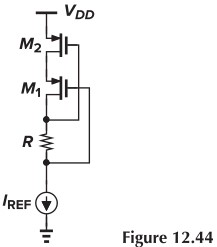
12.7 Consider the self-biased cascode shown in Fig. 12.44. Determine the minimum and maximum values of $RI_\tx{REF}$ such that both $M_1$ and $M_2$ remain in saturation

Solution: To make $M_1$ remain saturation,
\[V_{D1}-V_{G1} \leq \vert V_\tx{TH1} \vert\\ \Rightarrow RI_\tx{REF} \leq \vert V_\tx{TH1} \vert\]To make $M_2$ remain saturation
\[V_{G1}+\vert V_{GS1} \vert - V_{G2} \leq \vert V_\tx{TH2} \vert\\ \Rightarrow RI_\tx{REF} \geq \vert V_{GS1} \vert - \vert V_\tx{TH2} \vert\]In summary,
\[\vert V_{GS1} \vert - \vert V_\tx{TH2} \vert \leq RI_\tx{REF} \leq \vert V_\tx{TH1} \vert\]