振荡作业

1. Explain Barkhausen criteria?

振荡的两个条件：环路增益 $\beta H$ 满足

1. 相位为 0（360）
2. 幅度大于等于 1

---

1. Explain why one-stage and two-stage system can not oscillate, while three-stage system can oscillate

分析步骤：

1. 判断 dc phase shift
2. 判断 pole 带来的 phase shift
3. 把 1 和 2 相加，看在 $(0,\infty)$ 内 total phase shift 能否够 360 （并且 360 时不能在 0 或 $\infty$）
4. 判断在 360 时 gain 是否大于等于 1

---

1. Explain briefly the oscillating principle of the three-stage CMOS converters.

简单来说就是每个反相器带一个极点，当每个极点贡献 $60^\circ$ 时，总相位为 $(60^\circ+180^\circ)\times 3 = 720^\circ$，符合振荡条件。

---

1. What is the maximum voltage swing for Vx or Vy?（Figure 15.12，即三个差分管的振荡器，X、Y 指两个差分输出）

这不就是之前说过的嘛！最大时是 $V_{DD}$，最小时是 $V_{DD}-R I_{SS}$

---

1. Why four-stage single-ended ring oscillator can not oscillate, while four-stage differential ring oscillator can oscillate?

• 4 single-ended: 本身反相的延时为 720°，而极点的延时为 0~360°，总相位在 0 或无穷远处达到 360，能振起来才怪！
• 4 differential：把最后一级反过来，使其正常放大，则本身反相的延时仅为 $540^\circ$，加上极点的延时为 0~360°，可以达到 720 度！

顺便吐槽一下这题，4 single-end 的最后一级改为 Source Follower 不也一样的吗……

---

15.13 The stage of Fig. 15.45 is designed with $I_T = 1\text{mA}$ and $(W/L)_{1,2} = 50/0.5$. Assume that $I_H\gg I_1$.

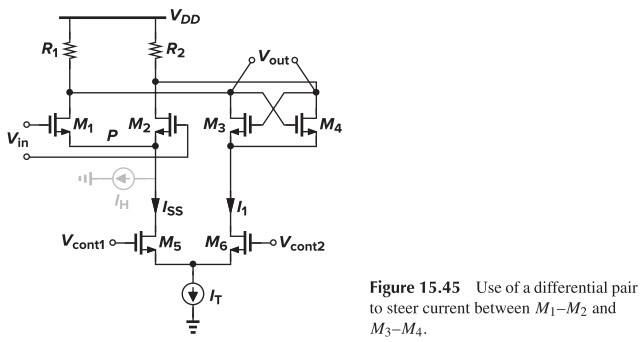
(a) Determine the minimum value of $R_1 = R_2 = R$ to ensure oscillation in a three-stage ring.

(b) Determine $(W/L){3,4}$ such that $g{m3,4}R = 0.5$ when each of $M_3$ and $M_4$ carries $I_T/2$.

(c) Calculate the minimum value of $I_H$ to guarantee oscillation.

(d) If the common-mode level of $V_\text{cont1}$ and $Vcont2$ is 1.5 V, calculate $(W/L){5,6}$ such that $I_T$ sustains 0.5 V when $V\text{cont1} = V_\text{cont2}$.

Solution:

(a) To make a three-stage ring oscillate, the minimum gain of each stage is 2, i.e. $g_{m1,2} R=2$, therefore

\[R = \frac{2}{g_{m1,2}}\\ \begin{aligned} g_{m1,2} &= \sqrt{\mu_n C_{ox} (W/L)_{1,2} I_T}\\ &= \sqrt{1.34225\times 10^{-4}\times 50/0.5\times 1\times10^{-3}}\\ &=3.66\times 10^{-3} \end{aligned}\\ \therefore R = 546\] \[R= \frac{R_N R_P}{R_N-R_P}=\frac{R_{1,2}}{1-g_{m3,4}R_{1,2}} \gt R_{1,2}\]

the minimum value of $R_{1,2}$ is 546.

(b)

\[\frac{g_{m3,4}}{g_{m1,2}} = \sqrt{\frac{(W/L)_{3,4}}{(W/L)_{1,2}} } = \frac{0.5/R}{2/R} = 0.25\\ \Rightarrow (W/L)_{3,4} = 0.25^2 (W/L)_{1,2}\]

(c)

\[\vert A_v \vert = g_{m1,2}R = g_{m1,2} \frac{R_{1,2}}{1-g_{m3,4} R_{1,2}} \geq 2\\ \Rightarrow g_{m1,2} R_{1,2} \geq 2(1-g_{m3,4} R_{1,2})\\ \Rightarrow \sqrt{I_H(W/L)_{1,2}} \cdot R_{1,2} \geq 2(1-\sqrt{I_T (W/L)_{3,4}} \cdot R_{1,2})\\ \downarrow\\ I_H \geq \left[ \frac{2(1-\sqrt{I_T (W/L)_{3,4}} \cdot R_{1,2})}{\sqrt{(W/L)_{1,2}} \cdot R_{1,2}} \right]^2\]

(d)

\[\frac{I_T}{2} = \frac{1}{2} \mu_n C_{ox} (W/L)_{5,6} (V_{GS5,6}-V_{TH5,6})^2\\ \Rightarrow (W/L)_{5,6} = \frac{I_T}{\mu_n C_{ox} (V_{GS5,6}-V_{TH5,6})^2}\\ V_{GS5,6}+0.5 \text{V} = 1.5 \text{V}\]