原题
3.17 Sketch $V_\tx{out}$ versus $V_\tx{in}$ for the circuits of Fig. 3.80 as $V_\tx{in}$ varies from 0 to $V_\tx{DD}$. Identify important transition points.(a,b 很简单,关键是 c,d 有点问题)
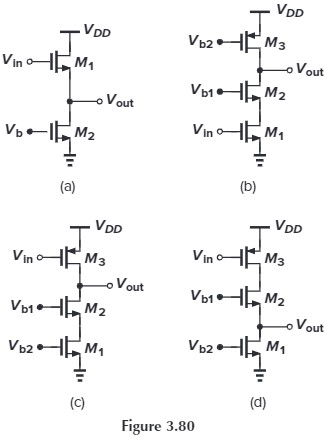
答案
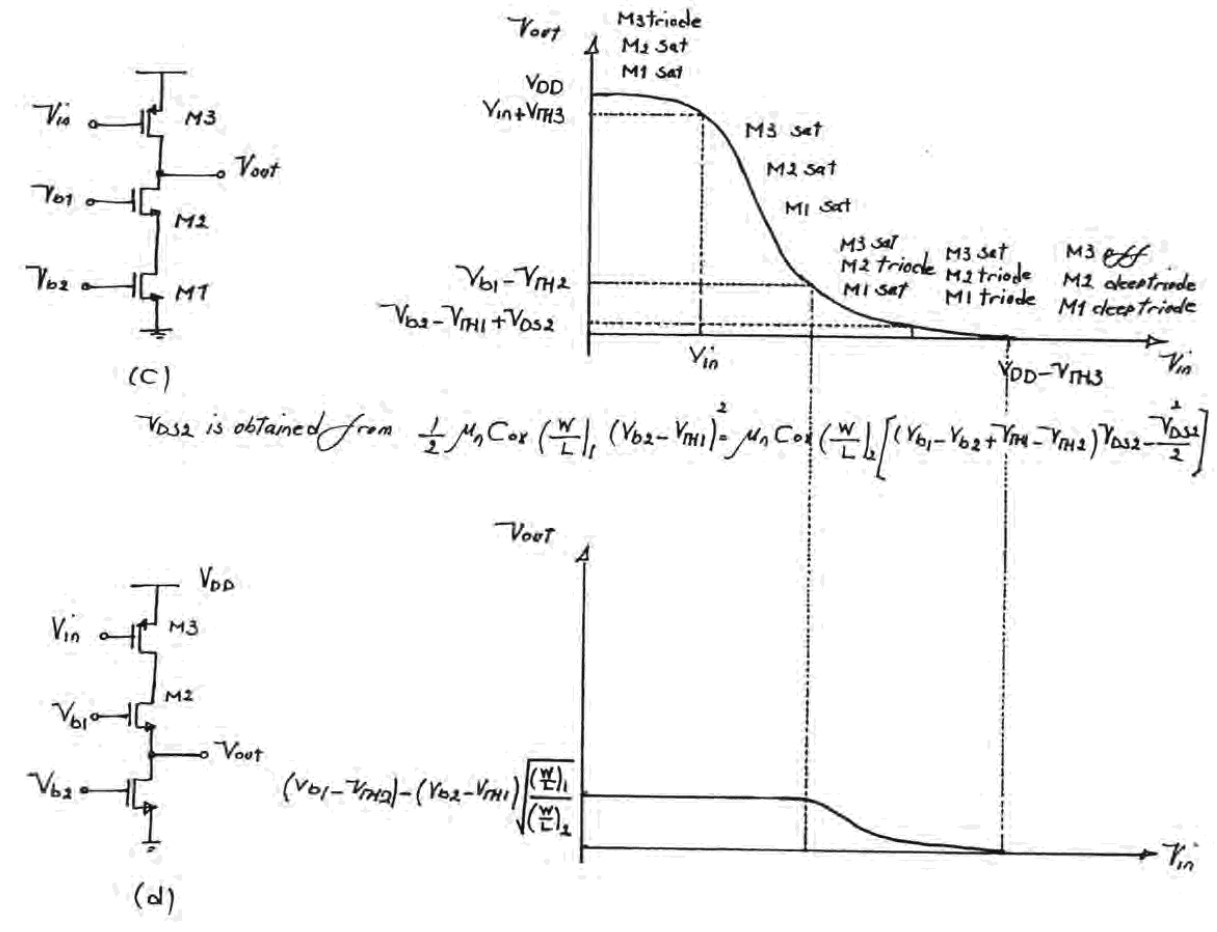
关于 (d) 中的 $V_\tx{out}$ 那个值的求解:
\[(W/L)_2 (V_{b1}-V_\tx{out}-V_\tx{TH1})^2 = (W/L)_1 (V_{b2}-V_\tx{TH2})^2\\ 解得:V_\tx{out} = (V_{b1}-V_\tx{TH1})-\sqrt{\frac{(W/L)_1}{(W/L)_2}}(V_{b2}-V_\tx{TH2})\]仿真
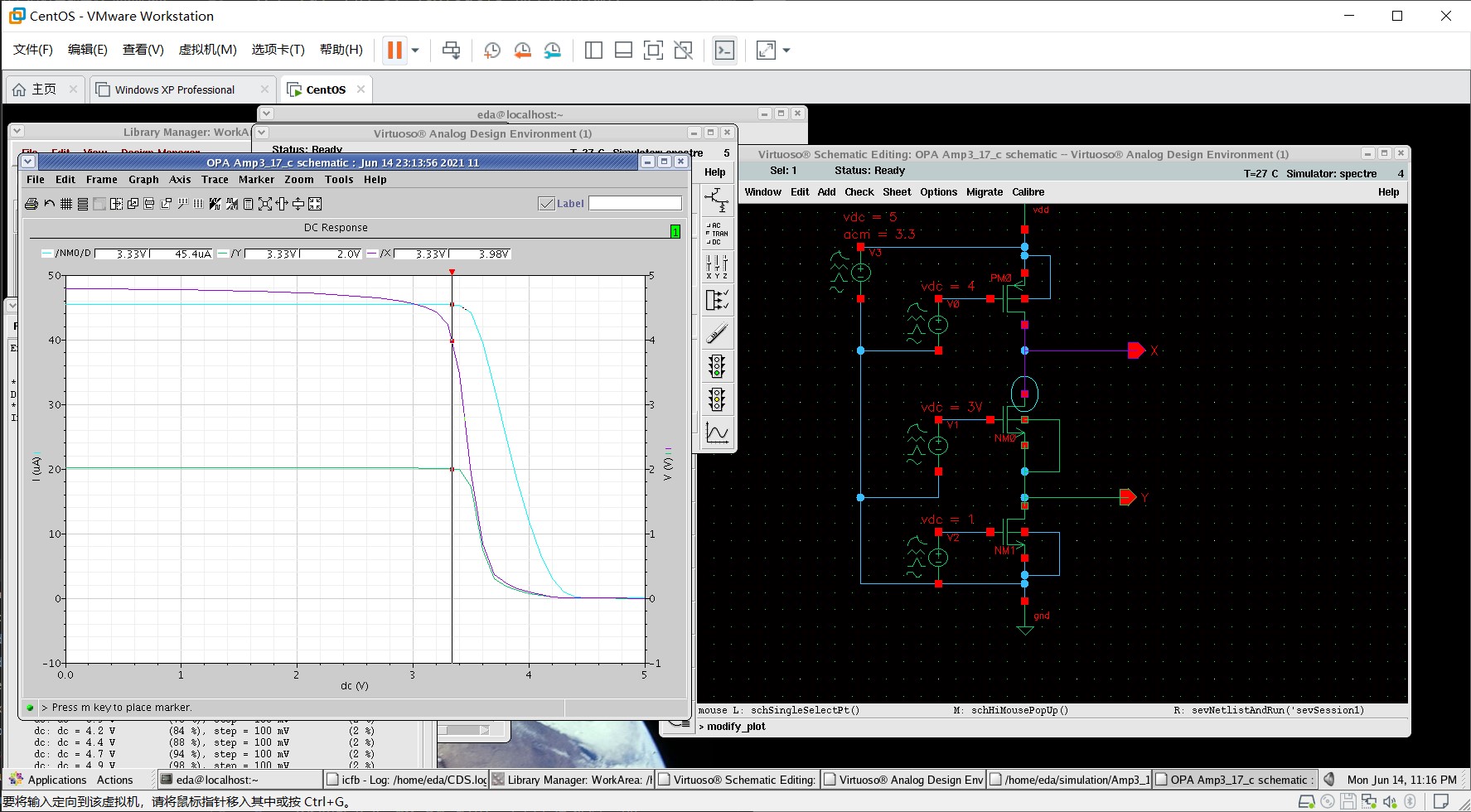
- 工艺:Chrt35rf
- M1、M2、M3 W/L = 1u/350n
分析
我们设 (c) 中输出为 $V_X$,(d) 中输出为 $V_Y$(对应仿真中的 X、Y 端口)
不妨先考虑三个管子均饱和的情况,根据答案,应该对应 $Y$ 曲线水平部分。此时,若减小 $V_\tx{in}$(增大 $\vert V_{GS3} \vert$),根据 $I_{D3}=\frac{1}{2}K_p(W/L) (V_{GS3}-V_\tx{TH3})^2$,$I_D$ 会变大。但注意到仿真中,电流也是水平不变的,这就产生了矛盾,说明有两种可能:
- 可能要考虑 $M_3$ 的沟道长度调制效应,即:$I_{D3}=\frac{1}{2}K_p(W/L) (V_{GS3}-V_\tx{TH3})^2(1-\lambda V_{DS3})$
- 可能此处并非 $M_3$ 饱和,而是在线性区,即:$I_{D3}=K_p (W/L)[(V_{GS3}-V_\tx{TH})V_{DS3}-\frac{1}{2}V_{DS3}^2]$
观察此时 $V_X$ 的电压,当 $V_\tx{in}=3.3V$ 时,$V_X\approx 3.9V$,我们几乎可以认为 $\vert V_{GD3}\vert \geq \vert V_\tx{TH3} \vert$,即 $M_3$ 应该处于线性区。为了进一步验证这个结论,我们可以作出理论上的 $V_X$ 曲线:下图绿线对应线性区,灰线对应饱和区。注意到绿线和仿真曲线(紫色那条)几乎拟合,这基本上可以证明 $M_3$ 确实是在线性区(而非答案所说的饱和区)
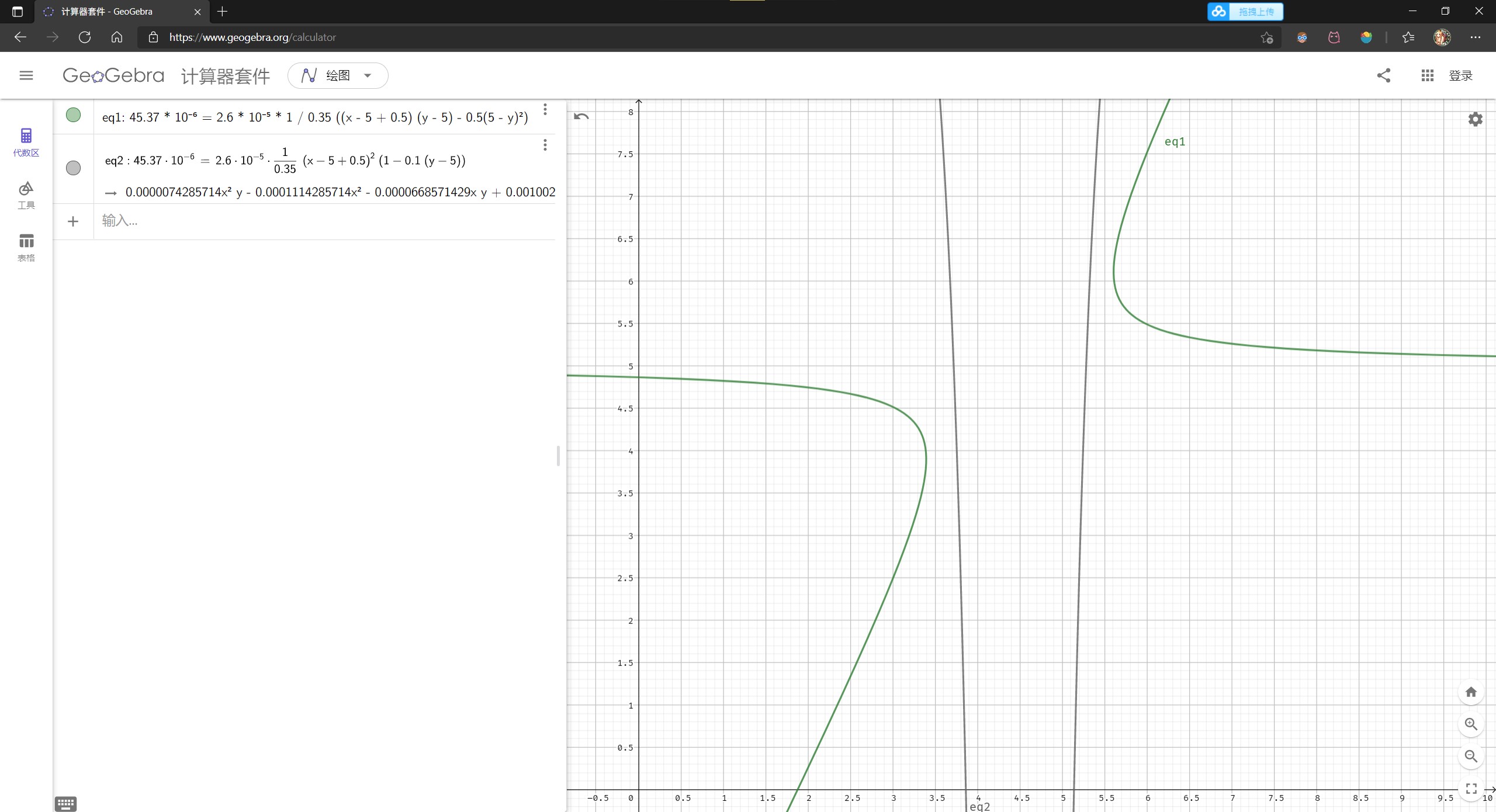
那么,$M_3$ 饱和区在哪呢?个人认为,应该对应仿真图中,$V_X,V_Y$ 不重合那一段($V_\tx{in}=3.3\sim 3.6 \tx{V}$),此时 $V_X$ 相当于 $M_3$ 的共源输出,并且 $M_2$ 同样饱和,所以共源增益应该比较大。而 $V_Y$ 由于受到 $M_2$ 的屏蔽,电压变化幅度不如 $V_X$
当 $M_2$ 进入线性区后,$V_Y$ 失去的屏蔽,故 $V_Y,V_X$ 相近,两曲线几乎重合。不过所幸 $M_1$ 依然是饱和,所以 $M_3$ 的共源增益依然较大,曲线的斜率依然较大。
当 $M_1$ 进入线性区后,$M_3$ 的共源增益减小,曲线斜率逐渐下降,直到 $M_3$ 关闭,斜率归零。
最终我认为应该是下图这样:
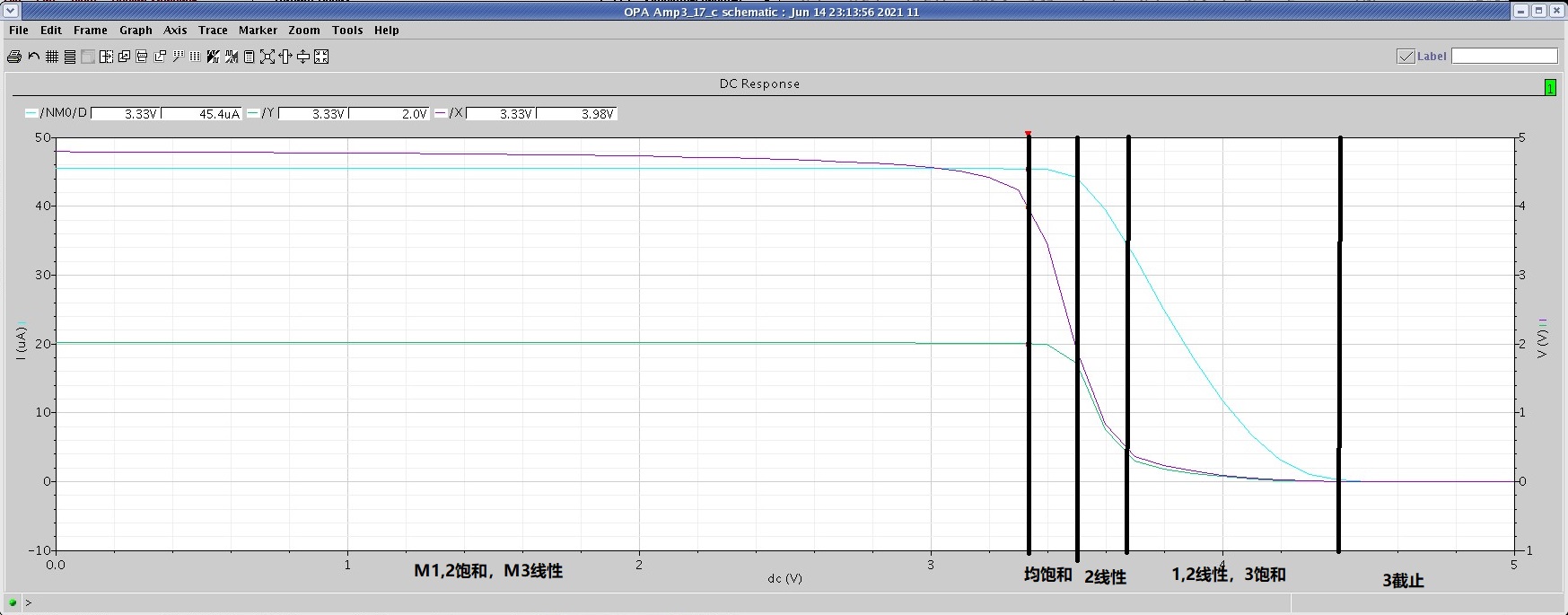
补充:三管均饱和时,$V_\tx{in}$ 变化会导致电流 $I_{D}$ 变化,但 $V_{GS1}$ 却是固定的,如果不考虑 $M_1$ 的沟道长度调制效应,那么 $I_{D1}$ 不会变,这两者不是矛盾了吗?也就是说我们应该考虑 $M_1$ 的沟道长度调制效应(同理,$M_2$ 也要考虑)原答案没有考虑这点,所以出错了。