\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\p}{\partial}
\end{align*}\]
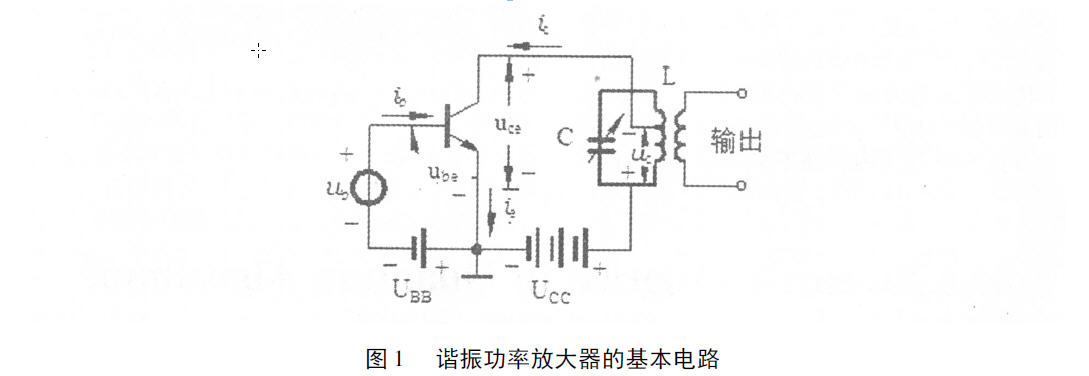

谐振功率放大器的工作原理
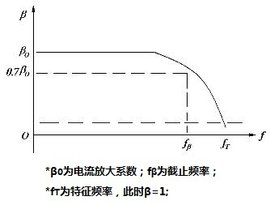
晶体管的工作频率范围分为:
- 低频区 $f<0.5f_\beta$:不考虑电抗分量与载流子渡越时间
- 中频区 $0.5f_\beta<f<0.2f_T$:考虑结电容
- 高频区 $0.2f_T<f<\beta<f_T$:考虑电极引线的电感作用
获得高效率
设:
- $P_=$:直流电源供给的直流功率
- $P_o$:交流输出信号功率
- $P_c$:集电极耗散功率
三个功率满足:$P_= = P_o+P_c$,我们定义集电极效率为:
\[\eta_c = \frac{P_o}{P_=}=\frac{P_o}{P_o+P_c}\]为了提高功率,我们必须减小 $P_c$ 或 增大 $P_o$。下面讨论如何减小集电极耗散。

集电极耗散功率等于集电极电压 $v_c$ 乘 集电极电流 $i_c$,即 $P_c=i_c\cdot v_c$。如果 $i_c$ 只在 $v_c$ 最低时才通过,则耗散功率会减小。我们将 $i_c$ 导通的范围称为导通角。比如(一定要分清图上的符号):
 | 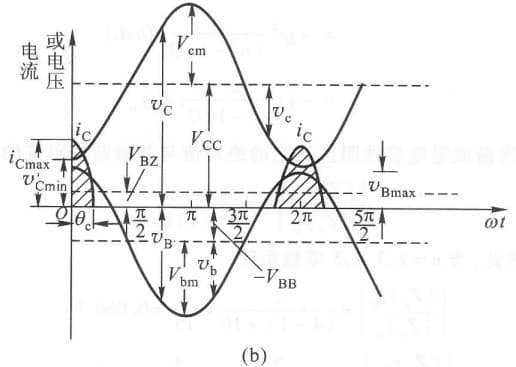 |
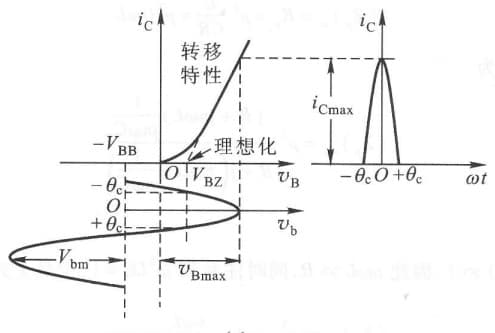
我们对转移特性曲线(集电极电压恒定,集电极电流与基集电压的关系曲线)进行折线化,只有当 $v_b$ 大于导通电压 $V_{BZ}$ 时,才有 $i_c$,则导通角为 $\theta_c$。将 $\theta_c$ 称为 半流通角 或 截止角,简称为 通角。
\[\because V_{bm}\cos\theta_c = V_{BZ}+V_{BB}\\ \therefore \cos\theta_c = \frac{V_{BZ}+V_{BB}}{V_{bm}}\]符号解释:
- $V_{CC}$ 集电极直流电源电压
- $V_{BB}$ 基级直流偏压
- $v_c$ 集电极交流输出电压
- $v_b$ 基级交流信号
- $v_C$ 集电极到发射级的瞬时电压
- $v_B$ 基级到发射级的瞬时电压
- $i_C$ 集电极瞬时电流
- $i_B$ 基级瞬时电流
- $i_E$ 基级瞬时电流
- $2\theta_c$ 集电极流通角
功率关系
已知:
\[v_C=V_{CC}-V_{cm}\cos\omega t\\ v_B=-V_{BB}+V_{bm}\cos\omega t\\\]集电极电流可以分解为傅里叶级数:
\[i_C=I_{C0}+I_{cm1}\cos\omega t+I_{cm2}\cos2\omega t+\cdots\\\]回路对基频谐振,此时的负载可以看作纯阻,所以输出基频功率为:
\[P_o=\frac{1}{2}V_{cm}I_{cm1}=\frac{V_{cm}^2}{2R_p}=\frac{1}{2}I_{cm1}^2R_p\]直流电源的直流功率为:$P_= = V_{CC}I_{C0}$
集电极效率:
\[\eta_c = \frac{P_o}{P_=}=\frac{\frac{1}{2}V_{cm}I_{cm1}}{V_{CC}I_{C0}}\]折线近似分析法
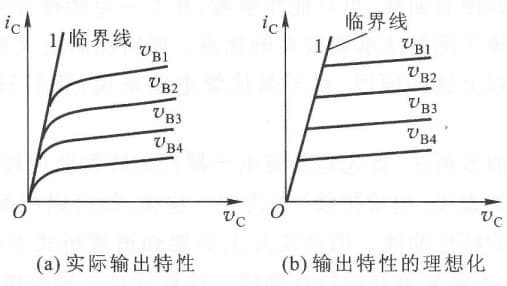
输出特性曲线:基集电压恒定,集电极电流与集电极电压的关系曲线
在低频中,我们将曲线分为:饱和区、放大区、截至区。而在高频中,我们将饱和区称为 过压工作状态,放大区称为 欠压工作状态,分界线称为 临界线。这个欠压/过压指的是交流输出的电压(也就是负载上的电压)。
\[临界线方程:i_C=g_{cr}V_C\]
转移特性曲线:集电极电压恒定,集电极电流与基集电压的关系曲线
- 跨导:$g_c=\frac{\Delta i_C}{\Delta v_B} \Big\vert_{v_C为常数}$
- 理想特性:$i_C=g_c(v_B-V_{BZ})$ (适用于 $v_B>V_{BZ}$)

动态特性与负载特性

外部电路关系式:
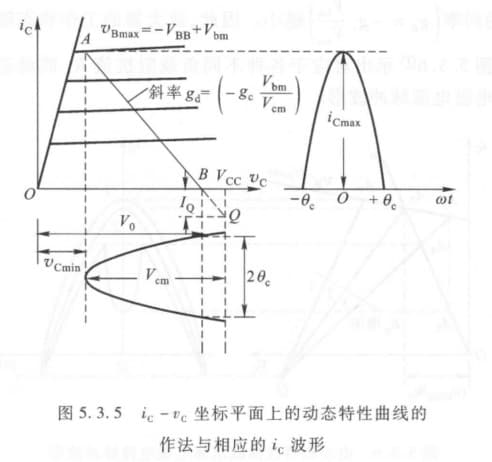
\[v_C=V_{CC}-V_{cm}\cos\omega t\\ v_B=-V_{BB}+V_{bm}\cos\omega t\\ \therefore v_B=-V_{BB}+V_{bm}\frac{V_{CC}-v_c}{V_{cm}}\]转移特性曲线折线化方程:
\[\begin{align} i_C&=g_c(v_B-V_{BZ})\\ &=g_c\left[-V_{BB}+V_{bm}\frac{V_{CC}-v_C}{V_{cm}} -V_{BZ} \right]\\ &=-g_c\left( \frac{V_{bm}}{V_{cm}} \right)\left[ v_C-\frac{V_{bm}V_{CC}-V_{BZ}V_{cm}-V_{BB}B_{cm}}{V_{bm}}\right]\\ &=g_d(v_C-V_0) \end{align}\] \[g_d=-g_c\left( \frac{V_{bm}}{V_{cm}} \right)\quad V_0=\frac{V_{bm}V_{CC}-V_{BZ}V_{cm}-V_{BB}B_{cm}}{V_{bm}}\]我们可以将其与输出特性曲线作在一起:

下面我们来讨论一下改变不同参数时,对电路工作状态的影响。