LCR回路中的瞬变现象
对于LCR回路的零输入响应,我们可以列出 KVL 式:
\[L\frac{\dif i}{\dif t}+Ri+\frac{1}{C} \int i\dif t=0\\ \rightarrow \frac{\dif^2 t}{\dif t^2}+\frac{L}{R}\frac{\dif i}{\dif t} + \frac{1}{LC} i=0\]我们定义 $\delta=\frac{R}{2L}$ 为回路的衰减系数,$\omega_0=\frac{1}{\sqrt{LC}}$ 为回路的固有角频率。从而得到下式:
\[\frac{\dif^2 t}{\dif t^2}+2\delta\frac{\dif i}{\dif t} + \omega_0^2 i=0\]这是一个常系数线性ODE方程,其通解为 $i=C_1 e^{r_1 t}+C_2 e^{r_2 t}$,其中,$r_1,r_2$ 是特征根。再由初始条件:$\left. i \right\vert_{t=0}=0$ 和 $L \left( \frac{\dif i}{\dif t} \right)_{t=0}=0$,我们得到:
\[i=\frac{-V}{2L\sqrt{\delta^2-\omega_0^2}} e^{-\delta t} \left( e^{t\sqrt{\delta^2-\omega_0^2}}-e^{-t\sqrt{\delta^2-\omega_0^2}} \right)\]根据 $\sqrt{\delta^2-\omega_0^2}$ 的值,我们可以分成下列三种情况:
-
$\delta^2>\omega_0^2$,则:
\[i=\frac{-V}{L\sqrt{\delta^2-\omega_0^2}} e^{-\delta t}\sinh(\sqrt{\delta^2-\omega_0^2})\]此时称为过阻尼。
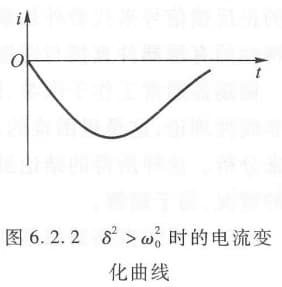
-
$\delta^2=\omega_0^2$,则:
\[i=\frac{-V}{L}te^{-\delta t}\]此时称为临界阻尼。
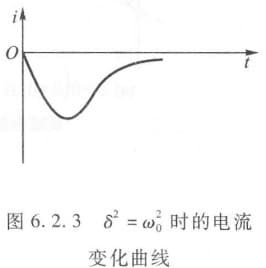
-
$\delta^2<\omega_0^2$,我们令 $j\omega=\sqrt{\delta^2-\omega_0^2}$ 则:
\[i=\frac{-V}{\omega L} e^{-\delta t} \sin\omega t\]此时称为欠阻尼(自由振荡),并可以进一步分为下面三种情况:
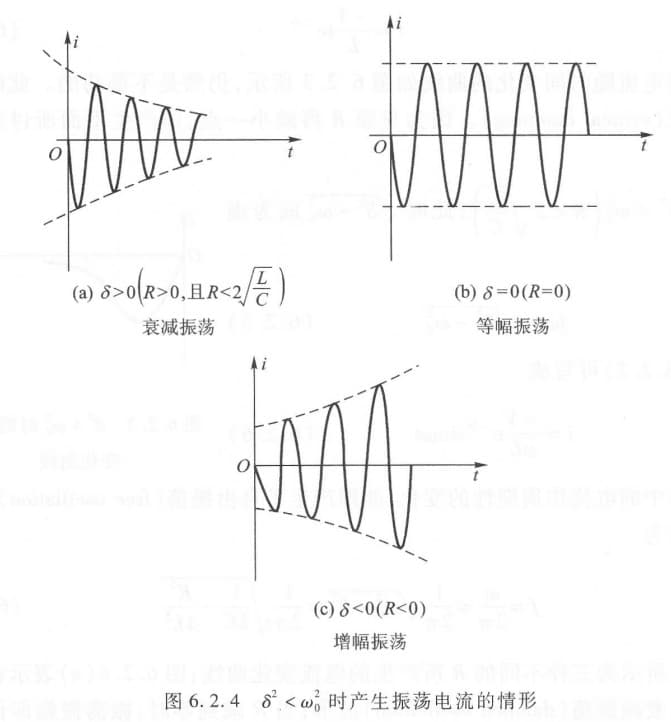
综上,为了获取等幅振荡,我们需要满足三个条件:
- 包含两个储能元件,一个释放能量,一个接收能量;(L、C)
- 必需使 R=0,也就是说,我们需要一个电源补充电路损失;(Vcc)
- 有一个控制电路,使电源在正确时刻补充能量损失。(晶体管和正反馈)
正反馈
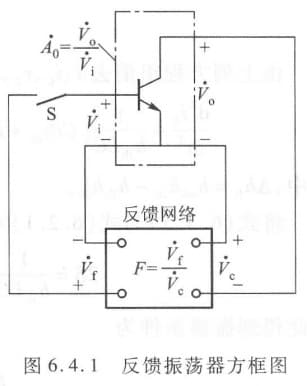
上图为反馈放大器的方框图。模电中已经知道,闭环增益为:
\[\dot{A}_f = \frac{\dot{A}_0}{1-\dot{A}_0\dot{F}}\]写一下下推导过程:
\[\dot{F}=\frac{\dot{V}_f}{\dot{V}_0}\quad \dot{A}_0=\frac{V_o}{V_i}\\ \dot{A}_f = \frac{\dot{V}_o}{\dot{V}_i-\dot{V}_f}=\frac{\dot{V}_o}{\frac{\dot{V}_o}{\dot{A}_0}-\dot{F}\dot{V}_0}=\frac{\dot{A}_0}{1-\dot{A}_0\dot{F}}\]振荡条件为:反馈系数 $\dot{F}=\frac{1}{\dot{A}_0}$ 或 $1-\dot{A}_0\dot{F}=0$,此时 $\dot{A}_f\rightarrow\infty$
振荡器的平衡与稳定条件
平衡条件
考虑到振荡器起振后,随着振荡幅度的不断增长,放大器从甲类迅速过渡到丙类工作状态
稳定条件
相位
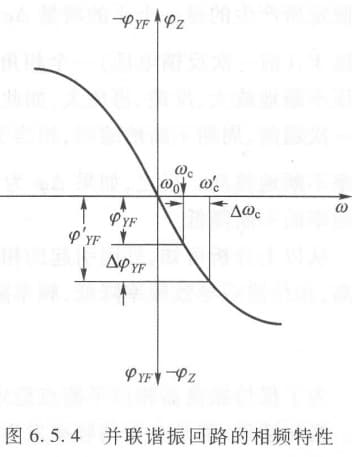
如果相位平衡遭到破坏,即 $\dot{V}_f$ 比原输入 $\dot{V}_i$ 超前 $\Delta \varphi$,周期就会缩短,频率 $\omega$ 就会增加,反之减小。也就是相位与频率的变化量满足 $\Delta \omega/\Delta \varphi > 0$。因此为了保持相位稳定,要使得 $\Delta \omega/\Delta \varphi < 0$,即:
\[\frac{\p \varphi}{\p \omega}<0\\\]一般忽略 $\varphi_Y+\varphi_F$,只
可见只有当相频特性曲线 $\varphi_z = f(\omega)$ 的斜率为负时,才能满足相位稳定条件。而恰好,LC并联谐振回路满足相频特性为负。
反馈型 LC 振荡器
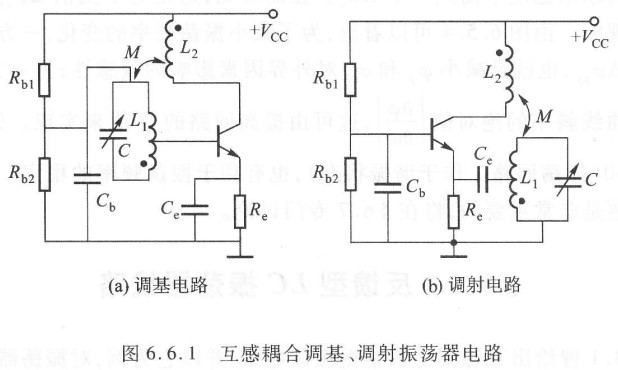
互感耦合振荡器
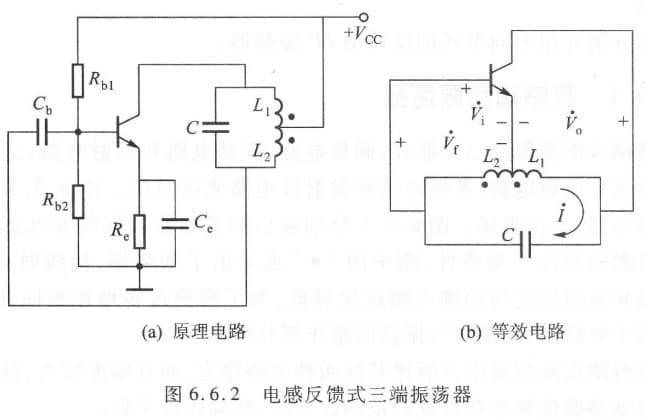
电感反馈式振荡器
又称为哈特莱振荡器。其优缺点如下:
- 优点:
- 容易起振
- 调整频率方便
- 缺点:
- 波形不够好
- 不适于很高频率工作
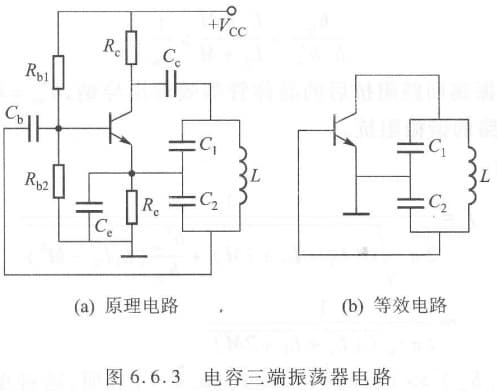
电容反馈式振荡器
又称为考毕兹振荡器。其优缺点如下:
- 优点:
- 振荡波形好
- 频率稳定性好,适合高频电路
- 缺点:
- 不方便通过电容来调整频率
LC三端式振荡器
我们将上面所讨论的振荡器总结成如下统一形式。我们假定 $Z_1,Z_2,Z_3$ 都是纯电抗 $X_1,X_2,X_3$。若要产生振荡,则回路要谐振,也就是 $X_1+X_2+X_3=0$
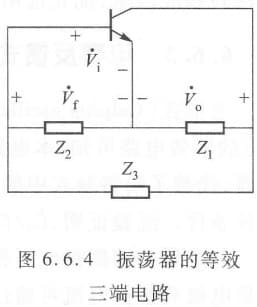
同时,为了满足 $\dot{V}_0$ 与 $\dot{V}_i$ 相位差为 180°,$X_1,X_2$ 必须是同性质,因而 $X_3=-(X_1+X_2)$ 必须是另一性质的电抗。
频率稳定性问题
我们定义频率准确度为 $f$ 与 $f_0$ 之间的偏差,进一步又分为绝对准确度和相对准确度:
- 绝对准确度:$\Delta f=f-f_0$
- 相对准确度:$\frac{\Delta f}{f_0}=\frac{f-f_0}{f_0}$
我们又定义频率稳定度,指在一定时间间隔内,频率准确度的变化,进一步分为:
- 短期
- 中期
- 长期
频率稳定度需要大量测量,可以用均方根值法来定量分析:
\[\sigma_n \sqrt{\frac{1}{n} \sum \left[ \frac{\Delta f}{f}_i - (\overline{\frac{\Delta f}{f})} \right]}\]