\[\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\p}{\partial}\]
直接调频
调频波的表达式:
\[a(t)=A_0 \cos \left[ \omega_0 t+k_f\int_o^t v_\Omega(t)\dif t \right]\\ =A_0\cos(\omega_0 t+\frac{k_f V_\Omega}{\Omega}\sin\Omega t)\]LC 自激振荡器产生载波,用调制信号去控制回路的电感或电容从而改变频率。
可以用变容二极管调频。当二极管反偏时,结电容 $C_j$ 与反向电压 $v_R$ 满足:
\[C_j =\frac{C_{j0}}{(1+\frac{v_r}{V_D})\gamma}\]$C_{j0}$ 时 $v_R=0$ 时的电容,$V_D$ 时势垒电位差,$\gamma\approx 1/2\sim1/3$ 是结电容变化指数,
设反向电压为:$v_R(t)=V_0+V_\Omega\cos\Omega t$
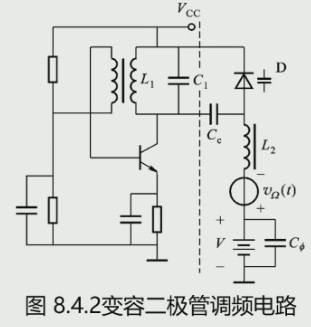
- 优点:
- 能获得较大频移
- 线路简单
- 几乎不需要调制功率
- 缺点:
- 中心频率稳定度较差(改善方法:用石英晶体、自动频率控制电路、锁相环电路)
间接调频
要想提高中心频率稳定度,也可以采用间接调频。
调相波的表达式:
\[a(t)=A_0\cos[\omega_0 t+k_pv_\Omega(t)]\\ =A_0\cos[\omega_0 t+k_pV_\Omega \cos \Omega t]\]对比调频波:$a(t)=A_0 \cos \left[ \omega_0 t+k_f\int_o^t v_\Omega(t)\dif t \right]$,可以看出,将调相波的输入信号换成积分就能得到调频波。也就是下图:
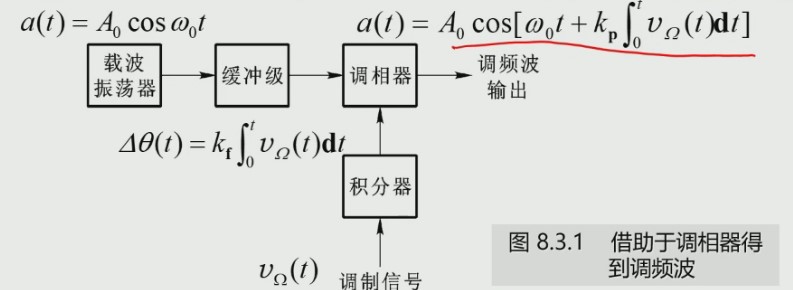
调相的方法有:
- 调制信号控制谐振回路或移相网络的电抗或电阻以实现调相
- 矢量合成法调相
- 脉冲调相
网络移相
6.7.5 有一个公式要看看
合成调相
当 $A_p$
\[a(t)=A_0\cos[\omega_0 t+k_pv_\Omega(t)]\\ =A_0 \cos (\omega_0t)\cos[A_pv_\Omega(t)]-\]脉冲调相
上两种调相方法的共同缺点是调制系数很小,需要加多级倍频器。而脉冲调相则无需倍频。