为什么要引入耦合回路?因为单回路振荡电路(串/并联振荡)的下降速度不够快。
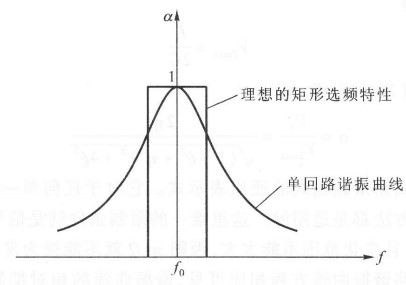
耦合回路
耦合回路(coupling circuit) 是由两个或以上的电路形成的一个网络,两个网络之间有公共阻抗。其中,接信号源的回路称为初基回路,接负载的回路称为次级回路。
用 耦合系数(coupling coeffient) 来衡量耦合程度,其定义为:公共电抗/电阻的绝对值与初级、次级回路中同性质的电抗/电阻的几何中项之比。
\[k = \frac{\rvert X_{12} \lvert}{\sqrt{X_{11}X_{22}}}\]显然耦合系数是一个小于等于1的正实数。
互感耦合回路
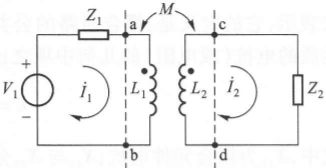
如图,我们列出两边的回路电压方程:
\[\dot{V}_1 = \dot{I}_1 (Z_1 + j\omega L_1) - \dot{I}_2(j\omega M)=\dot{I}_1 Z_{11} - j\omega MI_2\\ 0=\dot{I}_2 (Z_2 + j\omega L_2) - \dot{I}_1(j\omega M)=\dot{I}_2Z_{22} - j\omega MI_1\]解得:
\[\dot{I}_1=\frac{\dot{V}_1}{Z_{11}+\frac{(\omega M)^2}{Z_{22}}}\\ \dot{I}_2=\frac{j\omega M \dot{I}_1}{Z_{22}}=\frac{j\omega M \frac{\dot{V}_1}{Z_{11}}}{Z_{22}+\frac{(\omega M)^2}{Z_{11}}}\]显然,互感耦合相当于在初级回路中串联一个反射阻抗(reflected impedance)$(\omega M)^2/Z_{22}$,在次级回路中串一个电压源 $j\omega M \frac{\dot{V}_1}{Z_{11}}$ 和 反射阻抗 $\frac{(\omega M)^2}{Z_{11}}$
我们对其中一个反射阻抗进行讨论:
\[Z_{f1}=\frac{(\omega M)^2}{Z_{22}}=\frac{(\omega M)^2}{R_{22}+jX_{22}}=\frac{(\omega M)^2}{R_{22}^2+X_{22}^2}R_{22} - j\frac{(\omega M)^2}{R_{22}^2+X_{22}^2} X_{22}\\ =R_{f1}+jX_{f1}\]可以看出,反射电抗 $X_{f1}$ 与 $X_{22}$ 异号,说明反射阻抗与原阻抗相反。正是因为这个,所以在只有电感时也会产生振荡。
耦合振荡回路的频率特性
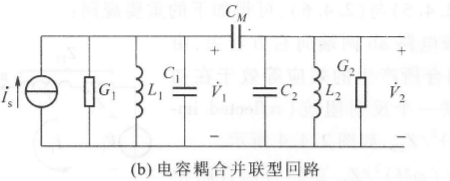
我们对上面的电容耦合回路进行分析(电感耦合也是类似的)
为了简化分析,我们假定 $L_1=L_2=L$,$C_1=C_2=C$,$G_1=G_2=G$,那么我们可以列出节点电流方程:
\[\dot{I}_s = \dot{V}_1 G + \frac{\dot{V}_1}{j\omega L}+j\omega(C_1 + C_M)\dot{V}_1-j\omega C_M \dot{V}_2\\ 0=\dot{V}_2G+\frac{\dot{V}_2}{j\omega L}+ j\omega(C_2+C_M)\dot{V}_2 - j\omega C_M \dot{V}_1\]我们将前三项广义失谐 $\xi = Q(\frac{\omega}{\omega_0}-\frac{\omega_0}{\omega})$ 来表示:
\[\dot{I}_s = \dot{V}_1 G(1+j\xi) - j\omega C_M \dot{V}_2\\ 0=\dot{V}_2 G(1+j\xi)-j\omega C_M \dot{V}_1\]解出 $V_2$:
\[\dot{V_2}=\frac{j\omega C_M \dot{I}_s}{G^2(1+j\xi)^2+\omega^2C_M^2}\] \[V_2=\frac{\omega C_MI_s}{G^2 \sqrt{(1-\xi^2+\frac{\omega^2C_M^2}{G^2})^2+4\xi^2}}\]注意到:
\[\eta=\frac{\omega C_M}{G}=\frac{\omega C}{G}\cdot\frac{C_M}{C}=Q\cdot k\\(k是耦合系数)\]于是我们把分母里那块疙瘩令为 耦合因数(coupling factor) $\eta = \frac{\omega C_M}{G}=Q\cdot k$,从而得到:
\[V_2=\frac{\eta I_s}{G \sqrt{(1-\xi^2+\eta^2)^2+4\xi^2}}\]那么谐振曲线最高点在哪呢?这个就别浪费时间计算了,直接用 MATLAB 看看吧!
syms xi eta
V = eta./( sqrt((1-xi.^2+eta.^2).^2 + 4*xi.^2) );
ezmesh(V,[-5 5 2*pi 0 5],100)
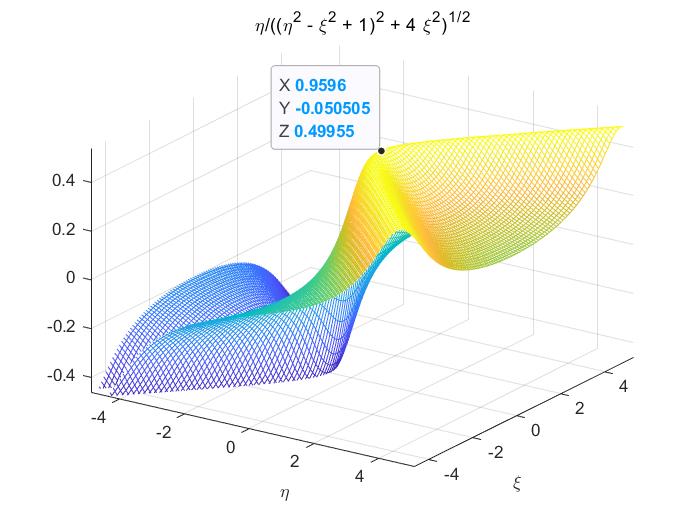
先说明一个东西,就是在 通频带附近,我们把 $\eta$ 和 $\xi$ 看作是两个独立的变量。尽管它俩的定义式中都有 $\omega$,但相比之下 $\eta$ 受 $\omega$ 影响较小,$\xi$ 改变时 $\omega$ 几乎没变。(书中这点没说清)
η≤1
带宽
观察图片可以知道,当 $\eta\leq1$ 时(图中那点以及左边部分),$V_{2}$ 在 $\xi=0$ 处取谐振曲线的最大值,并且在 $\eta=1$ 时取整个曲面的最大值,则 $V_{2\text{max}} = I_s/2G$,从而:
\[\alpha=\frac{V_2}{V_{2\text{max}}}=\frac{2\eta}{\sqrt{(1-\xi^2+\eta^2)^2+4\xi^2}}\]其中,$\alpha$ 定义为相对抑制比。我们可以求出 $2\Delta\omega_{0.7}$:
\[令 \eta=1, \alpha=\frac{1}{\sqrt{2}} 有\\ \alpha=\frac{1}{\sqrt{2}}=\frac{2}{\sqrt{4+\xi^4}}\\ 解得:\xi=\pm\sqrt{2}\\ \because \xi\approx Q\frac{2\Delta\omega_{0.7}}{\omega_0}\\ \therefore 2\Delta\omega_{0.7}=\sqrt{2}\frac{\omega_0}{Q}\Leftrightarrow \frac{\omega_0}{Q}(串/并联谐振)\]可以看出,耦合回路的通频带比串/并联谐振的更宽,因此谐振曲线更接近于矩形。
峰值
我们再考虑 $\eta$ 对 $V_{2}$ 峰值的影响,令 $\xi=0, \eta\leq1$,有:
\[\alpha = \frac{2\eta}{1+\eta^2} = \frac{2}{\frac{1}{\eta}+\eta} \leq 1\]显然,$\alpha$ 在 $\eta=1$ 时取最大值,并且 $\eta$ 减小时,$V_{2\text{max}}$ 减小(如下图)。
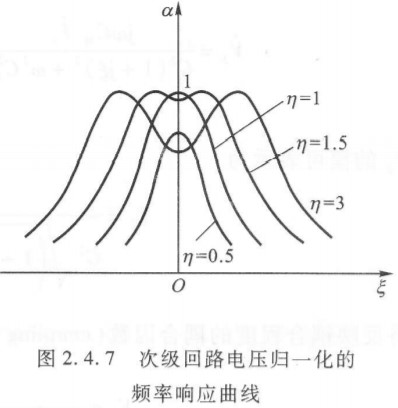
η>1
当 $\eta>1$ 时,可以发现 MATLAB 图中点右边部分中级凹下去,并且随着 $\eta$ 增大,两峰之间宽度越大。我们下面讨论谷深、峰宽和带宽。
谷深
显然谷对应的位置 $\xi=0$,和 $\eta\leq1$时峰的位置一样。所以我们可以套用上面公式: $\alpha=\frac{2\eta}{1+\eta^2}$,显然 $\eta$ 越大,谷越深。为了区分,我们用 $\delta$ 来衡量谷深:
\[\delta=\alpha=\frac{2\eta}{1+\eta^2}\\ (\delta越小,谷越深)\]峰宽
要求峰宽,我们需要求峰对应的 $\xi$。对 $\alpha=\frac{2\eta}{\sqrt{(1-\xi^2+\eta^2)^2+4\xi^2}}$ 求 $\xi$ 的导数,并令导数为0,我们不难算出:
\[\xi(1+\xi^2-\eta^2)=0\\ 解得: \begin{cases} \xi_0=0\\ \xi_1=-\sqrt{\eta^2-1}\\ \xi_2=+\sqrt{\eta^2-1} \end{cases}\\ 当且仅当 \eta\geq1 时有实根。\]则我们可以计算出两峰宽度 $\Delta \xi_1=2\sqrt{\eta^2-1}$,$\frac{\Delta f}{f_0}\approx k$(k是耦合系数)
带宽
接下来讨论带宽。计算方法还是相同的:
\[\frac{1}{\sqrt{2}}=\frac{2\eta}{\sqrt{(1-\xi^2+\eta^2)^2+4\xi^2}}\\ \Rightarrow \frac{1}{\sqrt{2}}=\frac{1}{\sqrt{(1+\eta^2)^2+2(1-\eta^2)\xi^2+\xi^4}}\\ 解出: \vert \xi \vert=\sqrt{\eta^2+2\eta-1}\\ 故:2\Delta f_{0.7}=\sqrt{\eta^2+2\eta-1} \cdot \frac{f_0}{Q}\]注意到谷深不能低于 $\frac{1}{\sqrt{2}}$,当 $\delta=\frac{2\eta}{1+\eta^2}=\frac{1}{\sqrt{2}}$ 时,$\eta=2.41$,从而:
\[2\Delta f_{0.7}=3.1\frac{f_0}{Q}\]由于 $\eta=Q\cdot k$,我们一般取 $k=1.5k_c$($k_c$ 指 $\eta=1$ 时的耦合系数,大小为 $k_c=\frac{1}{Q}$)
| 串/并联谐振 | 单峰耦合回路 | 双峰耦合回路 |
|---|---|---|
| $2\Delta f_{0.7}=\frac{f_0}{Q}$ | $2\Delta f_{0.7}=\sqrt{2}\frac{f_0}{Q}$ | $2\Delta f_{0.7}=3.1\frac{f_0}{Q}$ |
| 小 | 中 | 大 |
补充
比耦合回路性能更好的的滤波器可以采用如下方法:
- 巴特沃思(Butterworth)逼近
- 切比雪夫(Chebyshev)逼近
- 贝塞尔(Bessel)逼近
- 椭圆函数逼近