串、并联阻抗的等效互换
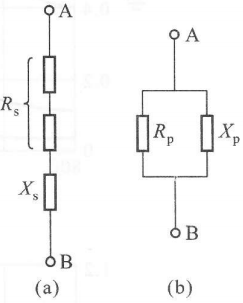
由图可列出(s-series; p-parallel):
\[\begin{align} R_s + jX_s &= \frac{R_p\cdot jX_p}{R_p+jX_p}\\ &=\frac{X_p^2}{R_p^2 + X_p^2} R_p + j\frac{R_p^2}{R_p^2 + X_p^2} X_p \end{align}\]解得:
\[R_s = \frac{X_p^2}{R_p^2 + X_p^2} R_p = \frac{X_p^2}{\vert Z_p \vert^2} R_p\\ X_s = \frac{R_p^2}{R_p^2 + X_p^2} X_p = \frac{R_p^2}{\vert Z_p \vert^2} X_p\]书上说:$Z_p^2 = R_p^2 + X_p^2$,但个人认为还是写成 $\vert Z_p\vert^2$ 好一点。
如果想要反过来,可以仿照上面:
\[\frac{R_s - jX_s}{R_s^2 + X_s^2} \leftarrow \frac{1}{R_s + jX_s} = \frac{1}{R_p} + \frac{1}{jX_p}\]解得:
\[R_p = \frac{R_s^2 + X_s^2}{R_s} = \frac{\vert Z_s\vert^2}{R_s}\\ X_p = \frac{R_s^2 + X_s^2}{Z_s} = \frac{\vert Z_s\vert^2}{X_s}\]也可以用品质因数 $Q$ 来表示以上式子(类比 $Q = \frac{\omega L}{R}$):
\[Q_L = \frac{X_s}{R_s} = \frac{R_p}{X_p}\] \[\begin{align}& \begin{cases} R_s &= \frac{1}{1+Q_L^2} R_p\\ X_s &= \frac{Q_L^2}{1+Q_L^2} X_p \end{cases}\\\\& \begin{cases} R_p &= (1+Q_L^2) R_s\\ X_p &= (1+\frac{1}{Q_L^2}) X_p \end{cases} \end{align}\]当 $Q_L > 10$ 时(高Q值),上式可改写成:
\[R_p \approx Q_L^2 R_s\\ X_p \approx X_s\]并联电路的广义形式
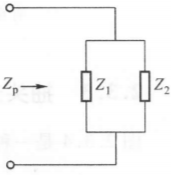
如图,我们可以列出总阻抗:
\[Z_p = \frac{Z_1Z_2}{Z_1+Z_2} = \frac{(R_1+jX_1)(R_2+jX_2)}{(R_1+jX_1)+(R_2+jX_2)}\]通常电路中 $X \gg R$,则在谐振时, $X_1+X_2=0$(类比 $\omega_0 L - 1/\omega_0 C$),进而:
\[\begin{align} Z_p &= \frac{(R_1 +jX_1)(R_2 + jX_2)}{R_1+R_2} \\ &\approx -\frac{X_1X_2}{R_1+R_2}\\ &= \frac{X_1^2}{R_1+R_2} = \frac{X_2^2}{R_1+R_2} \end{align}\]注意 注意上式成立的条件是 $X \gg R$ 和 $X_1+X_2=0$
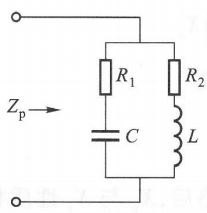
以上图为例,假设 $R_1, R_2$ 不大,我们可以计算出:
\[Z_p = = \frac{(\omega_p L)^2}{R_1+R_2} = \frac{(1/\omega_p C)^2}{R_1+R_2}\]与前一节并联谐振回路的公式比较($Z \approx \frac{\frac{L}{C}}{R + j(\omega L - \frac{1}{\omega C})}$),我们可以认为 $R_1$ 和 $R_2$ 集中在电感回路内。这一点在实际和做题中很有用。
抽头式并联电路
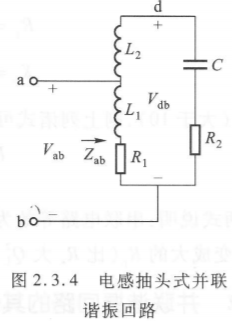
由广义并联电路: \(Z_{ab} = \frac{X_1^2}{R_1 + R_2} = \frac{(\omega_p L_1)^2}{R_1 + R_2}\)
我们定义 电感接入系数: \(\begin{align} p &= \frac{L_1}{L_1+L_2} \; \text{(无互感)}\\ &= \frac{L_1 \pm M}{L_1 + L_2 + 2M} \; \text{(有互感)} \end{align}\)
我们考察左边dab支路,可以得出 $p$ 的物理意义:
\[p =\frac{Ij\omega_p \cdot L_1}{Ij\omega_p \cdot (L_1 + L_2)} = \frac{V_{ab}}{V_{db}}\]回到最开始的 $Z_{ab}$,我们有:
\[Z_{ab} = \frac{(\omega_p L)^2}{R_1+R_2} p^2 = p^2Z_{bd}\]当抽头从低往高时,等效阻抗增大;从高往低时,等效阻抗减小。
注意到,一开始 $Z_{ab}$ 的式子的成立的条件是:$X \gg R$ 和 $X_1+X_2=0$,按道理这只适用于谐振情况,但实际上这不必满足谐振条件,只需 $X \gg R$ 。我们可以看看广义并联电路的阻抗:
\[Z_p = \frac{(R_1+jX_1)(R_2+jX_2)}{(R_1+jX_1)+(R_2+jX_2)}\]由于分子中可以忽略小的部分,分母中可以忽略大的部分,所以最终依然可以近似化成开头那条式。