\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\p}{\partial}
\end{align*}\]
元件分为:
- 线性元件(linear element)→常系数线性微分方程
- 非线性元件(non-linear element)→非线性微分方程
- 时变参量元件(time variation parameter element)→变系数线性微分方程
前面在小信号谐振的情况下,元件的非线性性可以忽略不计。但在放大器、振荡器、调制、解调中,有一个或多个器件工作在非线性状态,这些电路都是非线性电路。而变频器则是时变参量电路,因为其静态工作点的变换导致跨导随时间变换,我们后面会细讲。
非线性元件的特性
工作特性

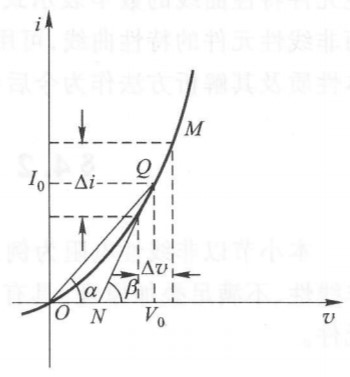
对于一般电阻,其动态电阻是恒定的;而对于二极管,其动态电阻始终在变化,即 $r=\lim_{\Delta r\rightarrow0} \frac{\Delta v}{\Delta i}$$=\frac{\dif v}{\dif i}=\frac{1}{\tan \beta}$,$\beta$ 是变值。
频率变化作用

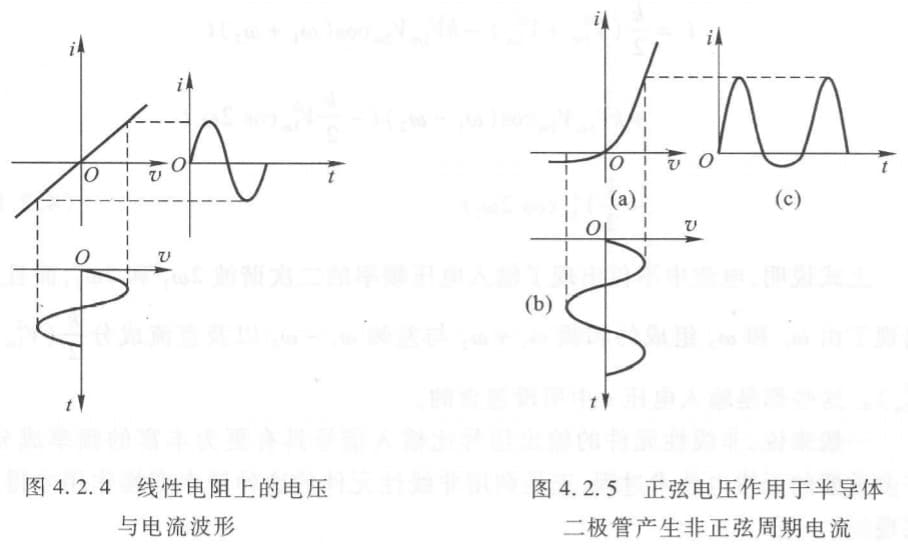
简单来说,就是一个标准正弦波经过非线性变换后不再是标准正弦波,因而含有其他谐波分量。比如,假设有一个元件满足 $i=v^2$,输入 $v=\sin t$,就会得到 $i=\sin^2t=(1-\cos 2t)/2$。更复杂的例子可以看教材。
不满足叠加原理
这个显而易见。
非线性电路分析简介
幂级数分析法
如果 $i=f(v)$ 在静态工作点 $V_0$ 附近各阶可导,我们可以将其展开为泰勒级数:
\[i = b_0+b_1(v-V_0)+b_2(v-V_0)^2+b_3(v-V_0)^3+\cdots\\ 其中,b_0=f(V_0),\; b_n=\frac{1}{n!}\left.\frac{\dif^n i}{\dif v^n} \right\vert\]在小信号,且特性曲线贴近于直线时,只取 0、1 次项:$i=b_0+b_1(v-V_0)$,从而可以当作线性来处理。但若特性曲线的曲率较大,则至少取前 3 项:$i = b_0+b_1(v-V_0)+b_2(v-V_0)^2$。如果信号很大,则就要取更高次项。(本课程最多取 4 项)
因此,幂级数分析法的一般步骤如下:
- 获取 i 和 v 的频率变换表达式
- 代入 v
- 用三角公式展开,得到频谱分量
- 由谐振回路和滤波器取出对应频率
折线分析法
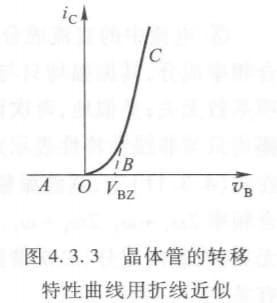
大信号下,幂级数会有较多项,分析起来不方便,所以我们干脆用多段折线近似替代特性曲线。比如对于下图,我们可用 AB,BC 两段直线代替:
\[\begin{cases} i_C=0 & (v_B\leq V_{BZ})\\ i_C=g_c & (v_B>V_{BZ}) \end{cases}\]
注意,折线分析法只能用于大信号!显然小信号在弯折处误差极大。在下一章还会进一步讨论折现分析法。