高频小信号放大器分为
- 谐振放大器
- 调谐放大器(高频放大器):对外界不同信号进行调谐
- 频带放大器(中频放大器):谐振频率固定不变
- 非谐振放大器
由于是小信号,所以我们依然能将晶体管看作线性元件,因此可以用二端口网络来等效分析。
我们用以下指标来衡量高频小信号放大器
增益(gain)
即放大倍数,有两种衡量方式:
- 电压增益:$A_v=\frac{V_o}{V_i}$,或 $A_v=20\lg\frac{V_o}{V_i}$
- 功率增益:$A_p=\frac{P_o}{P_i}$ 或 $A_p=20\lg\frac{P_o}{P_i}$
通频带
电压增益下降到最大值的 $\frac{1}{\sqrt{2}}$ 倍(或$-3$dB)时所对应的频率范围,记作 $2\Delta f_{0.7}$;
选择性(selectivity)
(1)矩形系数(rectangular coefficient)
\[K_{r0.1} = \frac{2\Delta f_{0.1}}{2 \Delta f_{0.7}}\\ K_{r0.01} = \frac{2\Delta f_{0.01}}{2 \Delta f_{0.7}}\]越接近于1越好,一般放大器的矩形系数在 2~5 内。
(2)抑制比(suppression ratio)
设 $A_{v0}$ 为谐振点 $f_0$ 的放大倍数,$A_v$ 为干扰 $f_0$ 的放大倍数。则定义抑制比:
\[d=\frac{A_{v0}}{A_v}\]用分贝表示,越大则抑制效果越好
工作稳定性(stability)
指工作状态发生变化时,放大器的主要特性的稳定程度。
噪声系数(noise figure)
见后面章节。在多级放大器中,最前面的一、二级对整个放大器的噪声系数起决定性作用,因 此要求它们的噪声系数尽量接近 1
晶体管高频小信号等效电路与参数
形式等效电路(网络参数等效电路)
形式等效电路(formal equicalent circuit)是将晶体管等效为有源线性四端口网络,优点是通用,缺点是网络参数与频率有关。
我们根据以前电路的学习,知道有 $h, y, z$ 三种参数系,我们下面用 $y$ 参考系来分析。
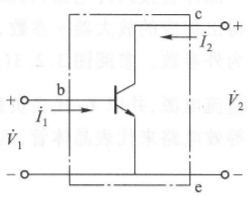 | $\Rightarrow$ | 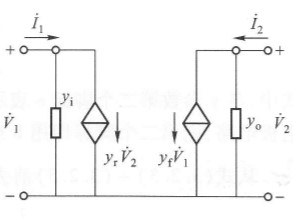 |
由图,有:
\[\dot{I}_1=y_i\dot{V}_1+y_r\dot{V}_2\\ \dot{I}_2=y_f\dot{V}_1+y_o\dot{V}_2\]其中,
- $y_i = \frac{\dot{I}_1}{\dot{V}_1}\big\vert _{\dot{V}_2=0}$ 输出短路时的输入导纳(input)
- $y_r = \frac{\dot{I}_1}{\dot{V}_2}\big\vert _{\dot{V}_1=0}$ 输入短路时的反向传输导纳(reflect)
- $y_f = \frac{\dot{I}_2}{\dot{V}_1}\big\vert _{\dot{V}_2=0}$ 输出短路时的正向传输导纳(forward)
- $y_o = \frac{\dot{I}_2}{\dot{V}_2}\big\vert _{\dot{V}_1=0}$ 输入短路时的输出导纳(output)
这四个导纳都可能是复数。下面我们用形式等效电路来分析电路:
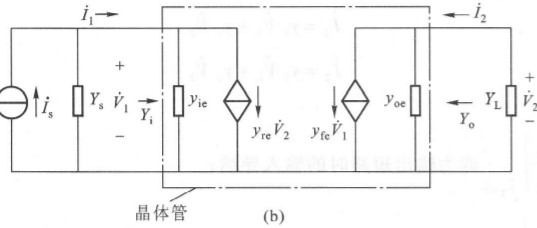
我们可以列出电流方程(式中,$y$的第二个角标表示该电路是共射):
\[\dot{I}_1=y_{ie}\dot{V}_1+y_{re}\dot{V}_2\\ \dot{I}_2=y_{fe}\dot{V}_1+y_{oe}\dot{V}_2\\ \dot{I}_2=-Y_L\dot{V}_2\]我们可以消去$\dot{V}_2$和$\dot{I}_2$:
\[\dot{I}_1=\Big( y_{ie} - \frac{y_{re}y_{fe}}{y_{oe}+Y_L}\Big)\dot{V}_1\]从而计算出输入导纳为:$Y_i=y_{ie} - \dfrac{y_{re}y_{fe}}{y_{oe}+Y_L}$,说明输入导纳与负载导纳有关。
同理,我们也可以选择消去 $\dot{V}_1$ 和 $\dot{I}_1$(需要将电源置零),不过更方便的,我们可以由对称性得到输出导纳:$Y_o=y_{oe}-\frac{y_{re}y_{fe}}{y_{ie}+Y_s}$
我们还可以由上面的电流方程得出电压增益:$\dot{A}_v=\frac{-y_{fe}}{y_{oe}+Y_L}$
混合π等效电路
我们将晶体管内部用RLC表示,得到混合π等效电路(hybrid π equivalent circuit)。优点是元件在很宽的频率范围内都保存常数,缺点是分析电路不够方便。
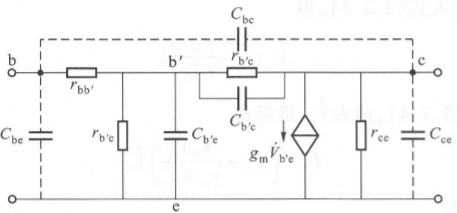
两种等效电路的转换
看书本65~67页。
晶体管的高频参数
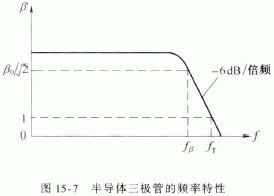
- 截止频率(cut-off frequency)$f_\beta$
- 电流放大系数 $\beta$ 值下降到 $\beta_0/\sqrt{2}$ 时的频率 $f_\beta$
当到截至频率时,$\beta$ 依然大于1,所以此时晶体管还能起作用(但已不在通频带内)
- 特征频率
- $\vert\beta\vert$ 下降到 1 时的频率 $f_T$
由以上关系式,我们有:
\[\vert\beta\vert=\frac{\beta_0}{\sqrt{1+(\frac{f}{f_\beta})^2}}\approx\frac{\frac{f_T}{f_\beta}}{\sqrt{1+(\frac{f}{f_\beta})^2}}\\ 若f\gg f_\beta,则:\\ \vert\beta\vert=\frac{f_T}{f}\]- 最高振荡频率 $f_{\text{max}}$
- 功率增益 $A_p=1$ 时最高工作频率 $f_{\text{max}}$,此时晶体管已得不到功率放大,无论什么方法都不能使晶体管振荡,所以叫最高振荡频率。
一般晶体管工作在 $\frac{1}{4}\sim\frac{1}{3} f_{\text{max}}$
三个频率的关系:$f_{\text{max}}>f_T>f_\beta$