\[\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\p}{\partial}\]
检波概述
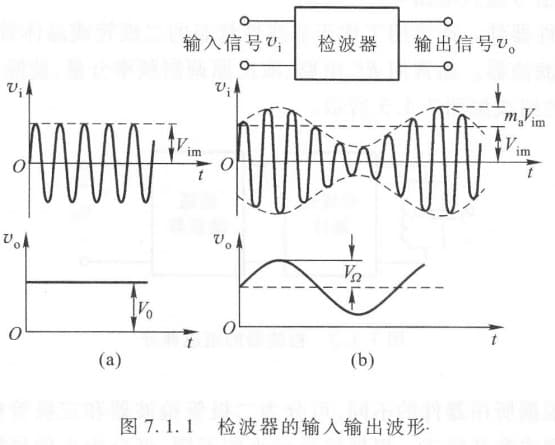
- 检波
- 从振幅受调制的高频信号中还原出原调制的信号。(检波是解调的一种,专门针对调幅)

检波器由三部分组成:
- 高频信号输入电路
- 非线性器件:将频谱从高频移到低频
- 低通滤波器:取出调制信号
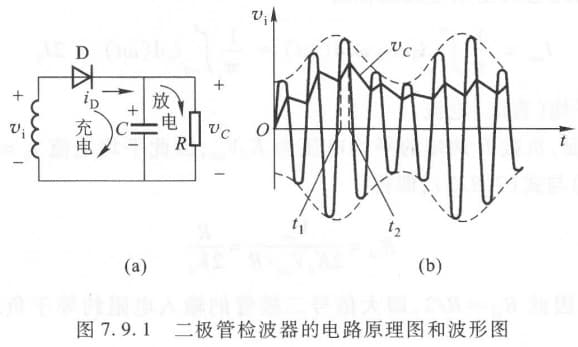
包络检波

质量指标
电压传输系数(检波效率):
\[K_d=\frac{输出低频电压V_{\Omega}}{输入调幅波包络振幅 m_a V_{im}}\]可以证明:
\[K_d=\cos \theta\\ \theta 导通角 \approx \sqrt[3]{\frac{3\pi R_d}{R}}\\ R 为负载电阻;R_d 为检波器内阻\]$K_d$ 是不随信号电压而变换的常数,当 $R \gg R_d$ 时,$\cos \theta \rightarrow 1$,$K_d \rightarrow 1$。
等效输入电阻
\[R_{id}=\frac{输入高频电压振幅V_{im}}{输入高频电流振幅I_{im}}\] \[I_{im}=\frac{1}{\pi} \int_{-\pi}^{\pi} i_d \cos \omega t\dif (\omega t)\approx \frac{1}{\pi} \int_{-\theta}^{\theta} i_d \dif(\omega t)=2 I_0\\ I_0=K_dV_{im}/R\\ \therefore R_{id}=\frac{V_{im}}{2K_d V_{im}/R}=\frac{R}{2K_d}\approx \frac{R}{2}\]由于二极管输入电阻影响,$Q$ 值降低,消耗一些高频功率
失真 包括:
- 惰性失真(对角线切割失真)、
- 时间常数 RC 太大,当包络朝较低值变换时,电容上的电荷来不及释放以跟踪其变化。
- 解决方法:选择合理的 RC,使得:$RC\Omega_\max < \frac{\sqrt{1-m_a^2}}{m_a}$
- 负峰切割失真(底边切割失真)
- 由于直流负载与交流负载不相等,而调幅度 $m_a$ 又较大,使得耦合电容 $C_c$ 放电较大,二极管提前截止,导致底部被切割。
- 非线性失真
- 检波二极管伏安特性曲线的非线性,使得输出音频电压不能完全和调幅波的包络成正比。
- 解决方法:选择较大的 $R$,使得非线性失真可以忽略
- 频率失真
- 电容随频率变化而引起的失真
- 耦合电容 $C_c$ 在低频 $\Omega_\min$ 处的阻抗不太大,滤波电容 $C$ 在 $\Omega_\max$ 时不产生旁路作用。即 $\frac{1}{\Omega_\max C}\gg R$,$\frac{1}{\Omega_\min C_c} \ll R$
同步检波
用于载波被抑制的双边带/单边带信号进行解调,特点是需要外加一个频率和相位与载波信号相同的信号。有相乘法与相加法两种。
乘积检波器
载波被抑制的双边带:$v_1=V_{1m} \cos \Omega t \cdot \cos \omega_1 t$
本地载波电压:$v_0=V_0\cos(\omega_0 t + \varphi)$
相乘输出:$v_2=v_1v_0$
滤除高频信号,得到 $v_\Omega=\frac{1}{2} V_{1m}V_0 \cos \varphi \cos \Omega t$
叠加型同步检波器
载波被抑制的单边带信号:$v_1=V_{1m} \cos (\omega_0+\Omega)t$
本地载波:$v_0=V_0\cos\omega_0 t$
两信号相加后:$v_2=v_1+v_0=V_m \cos (\omega_0 t+\theta)$
定义:$K_{f2}=\frac{二次谐波幅度}{基波幅度}$,这个值最好要小于 $2.5\%$