\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\p}{\partial}
\end{align*}\]
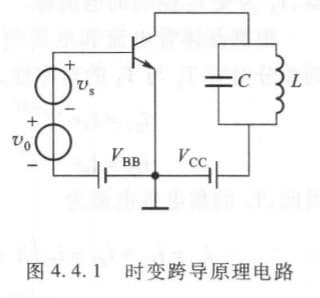
时变跨导电路分析

$v_0$ 是振幅较大的简谐振荡电压,$v_s$ 是振幅较小的任意形式电压信号。我们可以认为 器件参量受 $v_0+V_{BB}$ 控制,在 $v_0+V_{BB}$ 一定时,器件在 $v_s$ 变化范围内可视作线性,即工作点为:
\[v_B=V_{BB}+V_{0m}\cos\omega_0t\]我们设 $i_c=f(v_{BE})=f(v_B+v_s)$,用泰勒级数在 $v_B$ 点展开,得:
\[\begin{align} i_c\approx f(v_B)+f'(v_B)v_s\\ =f(V_{BB}+V_{0m}\cos\omega_0t)+f'(V_{BB}+V_{0m}\cos\omega_0t)\cdot V_{sm}\cos\omega_s t \end{align}\]模拟乘法器电路分析

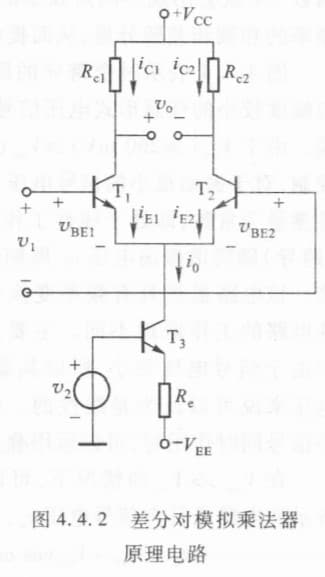
我们考虑上图中的差分对乘法器(differential multipler)。差分对管 $T_1$ 和 $T_2$ 的特性方程为:
\[i_{E1}=I_se^{q\,v_{BE1}/kT}\\ i_{E2}=I_se^{q\,v_{BE2}/kT}\]从而 $T_3$ 的集电极电流 $i_0$ 为:
\[\begin{align} i_0&=i_{E1}+i_{E2}=i_{E1}\left( 1+\frac{i_{E2}}{i_{E1}} \right)\\ &=i_{E1}(1+e^{-qv_1/kT}) \end{align}\]由上式,以及共基极电流放大系数的定义 $i_C=\alpha i_E$,我们有:
\[i_{C1}=\alpha i_{E1}=\frac{\alpha i_0}{1+e^{-z}}\\ i_{C2}=\alpha i_{E2}=\frac{\alpha i_0}{1+e^{z}}\]开关函数分析
某些电路中,非线性元件受大信号控制,轮换地导通或截止,此时大信号起到开关的作用。如下图,电路受大信号 $v_2=V_x\cos\omega_2t$ 控制:
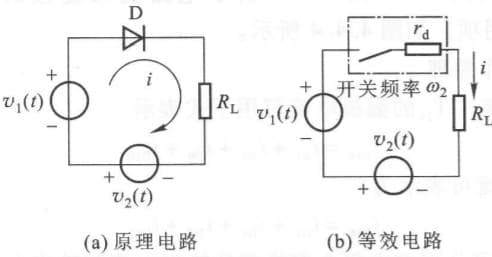
此时,电流的表达式为:
\[i= \begin{cases} \frac{1}{r_d+R_L}(v_1+v_2) & (v_2>0)\\ 0 & (v_2<0) \end{cases}\]可以看出,二极管相当于一个受 $v_2$ 控制的开关,即:
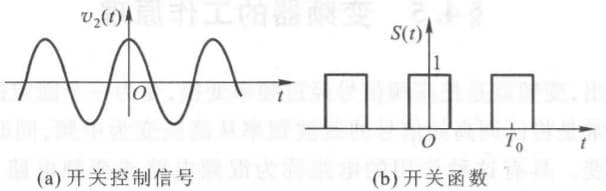
我们可以用开关函数表示二极管:
\[S(t)= \begin{cases} 1 & (v_2>0)\\ 0 & (v_2<0) \end{cases}\]从而,$i=\frac{1}{r_d+R_L}S(t)(v_1+v_2)$。
我们将 $S(t)$ 展开为傅里叶级数:
\[S(t)=\frac{1}{2} \left[ 1+\sum_{n=1}^{\infty} \frac{4\cdot(-1)^{n+1}}{(2n-1)\pi}\cos(2n-1)\omega_2t \right]\]并代入 $i$:
\[i=\frac{1}{2(r_d+R_L)} \left[ v_1+v_2+v_1\sum_{n=1}^{\infty} \frac{4\cdot(-1)^{n+1}}{(2n-1)\pi}\cos(2n-1)\omega_2t + v_2\sum_{n=1}^{\infty} \frac{4\cdot(-1)^{n+1}}{(2n-1)\pi}\cos(2n-1)\omega_2t \right]\]可以看出,电流 $i$ 中包含以下频谱:
- $\omega_1$,$\omega_2$ 原本的频率
- $\omega_1\pm(2n-1)\omega_2$,$n=1,2,\cdots$ 频率的和差
- $\omega_2\pm(2n-1)\omega_2$,$n=1,2,\cdots$,偶次谐波,包括直流
后续通过带通滤波器,就能得到所需的频率。