选频网络

作用 选出需要的频率分量和滤除不需要的频率分量

分类

\[\text{选频网络} \begin{cases} \text{振荡电路（由 L, C 组成）} { \begin{cases} \text{单振荡回路}\\ \text{耦合振荡回路} \end{cases} }\\ \text{滤波器} { \begin{cases} \text{LC集中滤波器}\\ \text{石英晶体滤波器}\\ \text{陶瓷滤波器}\\ \text{声表面波滤波器} \end{cases} } \end{cases}\]

振荡回路

由电感 L、电容 C 等电抗元件和外加电压组成的回路，其电流的大小和方向发生周期性变化

串联电路

串联振荡回路

信号源与电容串接的振荡回路

基本原理

  在高频中，电阻 R 主要来源于电感线圈，常忽略电容的损耗。

  上述电路的阻抗 Z 如下（电路内容）：

\[Z = R + \rm{j} (\omega L - \frac{1}{\omega C}) = \big| Z \big| \rm{e}^{\rm{j}\omega}\\ \big| Z \big| = \sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2}\\ \omega = \arctan \frac{\omega L - \frac{1}{\omega C}}{R}\]

  电抗 X 为：$X = \omega L - \dfrac{1}{\omega C}$

  回路中电流为：$\dot{I} = \dfrac{\dot{V_s}}{Z} = \dfrac{\dot{V_s}}{R + \rm{j} (\omega L - \frac{1}{\omega C})}$

  随着频率变化，电抗也随之变化。当满足谐振条件 $X = \omega_0 L - \dfrac{1}{\omega_0 C} = 0$ 时，串联回路 $Z_0 = R$，且为最小值，这时称为 串联谐振（series resonance），相应的谐振角频率和频率为：$\omega_0 = \dfrac{1}{\sqrt{LC}}$，$f_0 = \dfrac{1}{2\pi \sqrt{LC}}$ . 若此时外加电压 $\dot(V)$ 为常数，则有以下三个特性：

1. 谐振时，$Z_0 = R$，$\varphi = 0$，故电流达到最大值
2. 当谐振时，由 $\omega_0 L = \dfrac{1}{\omega_0 C}$，有：

\[\dot{V}_{L0} = \frac{\dot{V}}{R} \rm{j} \omega_0 L = \rm{j} \frac{\omega_0 L}{R} \dot{V}_s = \rm{j} Q \dot{V}_s \\ \dot{V}_{C0} = \frac{\dot{V}}{R} \frac{1}{\rm{j} \omega_0 C} = - \rm{j} \frac{1}{\omega_0 C R} \dot{V}_s = - \rm{j} Q \dot{V}_s\]

我们定义 $Q = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 C R} = \frac{1}{R} \sqrt{\frac{L}{C}}$，称为品质因数（quality factor）（注意是 shù 不是 sù）。从上两式可以得出两个结论：

1. 谐振时，电感与电容的电压大小是电源电压的 $Q$ 倍，因此要考虑元件耐压问题。这是串联谐振特有的现象，故串联谐振又称为电压谐振（voltage resonance）
2. 谐振时，电感与电容电压反相
3. 在谐振点及附近，电路电阻 R 决定电流大小；远离谐振点处，$\big\vert \omega L - \frac{1}{\omega C} \big\vert \gg R$（$Q$ 较大），电流与 R 无关。故我们可以画出不同 $R$（$Q$）时的 $I - \omega$曲线：

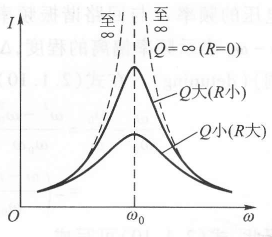
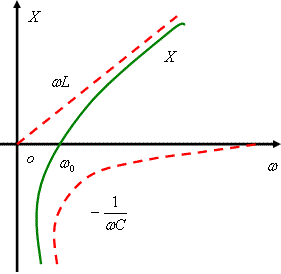
  若不满足谐振。当 $\omega < \omega_0$，有 $X = \omega L - \dfrac{1}{\omega C} < 0$，称为 容性；反之，当 $\omega > \omega_0$，有 $X = \omega L - \dfrac{1}{\omega C} > 0$，称为 感性

---

谐振曲线和通频带

谐振曲线：

\[\dot{N}(\omega) = \dfrac{\dot{I}(\omega)}{\dot{I}(\omega_0)} = \dfrac{R}{R + \rm{j} (\omega L - \frac{1}{\omega C})} = \dfrac{1}{1 + \rm{j} Q (\frac{\omega}{\omega_o} - \frac{\omega_0}{\omega})}\]

幅频特性曲线：

\[N(\omega) = \dfrac{I(\omega)}{I(\omega_0)} = \sqrt{\dfrac{1}{1 + Q^2 (\frac{\omega}{\omega_o} - \frac{\omega_0}{\omega})^2 }}\]

作出谐振曲线：

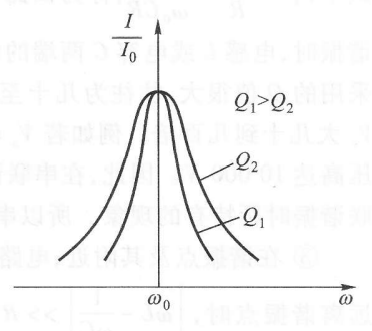
  可以看出，$Q$ 越大，在频率不变的情况下，谐振曲线越尖锐。为了描述尖锐程度，我们模仿高等数学中的“斜率”，引入以下概念：

失谐量（失调 detuning）：

失谐量 $\Delta\omega = \omega - \omega_0$

用来描述频率偏移程度

若 $\omega \rightarrow \omega_0$，有：

\[\begin{align*} \frac{\omega}{\omega_o} - \frac{\omega_0}{\omega} & = \frac{1}{\omega_0 \omega} (\omega + \omega_0)(\omega - \omega_0)\\ & = \frac{1}{\omega_0 \omega} (2\omega - \Delta\omega)(\Delta\omega)\\ & \approx \frac{2\Delta\omega}{\omega_0} \end{align*}\]

进一步我们可以定义，广义失谐（一般失谐 generalized detuning）：

$\xi = Q (\dfrac{\omega}{\omega_o} - \dfrac{\omega_0}{\omega}) \approx \rm{Q} \dfrac{2\Delta\omega}{\omega_0} = \rm{Q} \dfrac{2\Delta f}{f_0}$

谐振曲线的公式可以表示为：

\[N(\Delta\omega) = \frac{1}{\sqrt{1+\xi^2}} \approx \frac{1}{\sqrt{1+ (\rm{Q} \frac{2\Delta\omega}{\omega_0})^2 }}\]

上式称为 通用形式的谐振特性方程式，其成立条件是 $\omega \rightarrow \omega_0$ 或 $\Delta \omega \rightarrow 0$

---

当电流 $I = \frac{1}{\sqrt{2}} I_0$ 时，所对应的 $\omega_1, \omega_2$ 称为边界角频率，$\omega_2 - \omega_2$ 称为回路的通频带（passband）。这时，回路中所损耗的功率为谐振时的一半 故 $\omega_1, \omega_2$ 也称为半功率点。

因为 $\omega_1, \omega_2 \rightarrow \omega_0$，所以有：

\[\frac{I}{I_0} = \frac{1}{\sqrt{1+\xi^2}} = \frac{1}{\sqrt{2}}\\ \text{解得：} \xi_2, \xi_1 = \pm 1\]

进一步，因为 $\xi \approx \rm{Q} \dfrac{2\Delta\omega}{\omega_0}$，所以有：

\[\xi_2 - \xi_1 = \rm{Q} \dfrac{4\Delta\omega_{0.7}}{\omega_0} = 2\\ \Longrightarrow 2\Delta\omega_{0.7} = \frac{\omega_0}{Q} , 2\Delta f_{0.7} = \frac{f_0}{Q}\]

从上式可知，通频带与 $Q$ 值成反比，$Q$ 越高，谐振曲线越尖锐。这与前面的结论是一致的。

顺便说一句，从面我们还可进一步推出边界角频率的值，如下：

\[\frac{\omega}{\omega_o} - \frac{\omega_0}{\omega} = \frac{\xi}{Q} = \pm \frac{1}{Q}\\ \text{从而：}\omega^2 \mp \frac{\omega_0}{Q} \omega - \omega_0^2 = 0\\ \begin{align*} \text{解得：}\omega_2, \omega_1 &= \frac{\pm \frac{\omega_0}{Q} + \sqrt{\frac{\omega_0^2}{Q^2} + 4\omega_0^2}}{2}\\ &= \omega_0 \Big( \pm \frac{1}{2Q} + \sqrt{(\frac{1}{2Q})^2+1} \Big) \end{align*}\]

内阻与负载的影响

若增大回路电阻，会使得 Q 值降低

\[Q_L = \frac{\omega_0 L}{R + R_s + R_L}\]

并联电路

串联谐振回路适用于低内阻电源，如果电源内阻很大，则应采用并联谐振回路。

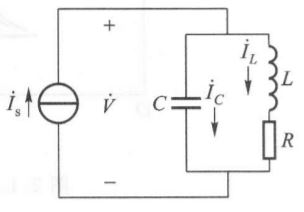
基本原理

并联谐振电路的阻抗表达式为：

\[Z = \frac{(R + j \omega L) \frac{1}{j\omega C} }{ R + j(\omega L - \frac{1}{\omega C})}\]

一般来说，$\omega L \gg R$（以后未说明则默认成立），我们可以忽略分子中的 $R$，所以：

\[Z \approx \frac{\frac{L}{C}}{R + j(\omega L - \frac{1}{\omega C})} = \frac{1}{\frac{CR}{L} + j (\omega C - \frac{1}{\omega L})}\]

若外加电流源为 $I_s$，则电压值为：

\[V = \frac{I_s}{ |Y| } = \frac{I_s}{\sqrt{(\frac{CR}{L})^2 + (\omega C - \frac{1}{\omega L})^2}}\]

由此可知，当电纳 $B = 0$时，$\dot{V}_0 = \frac{L}{CR} \dot{I}_s$，此时电压与电流同相，且达到最大值，此时总阻抗为纯阻，且为最大值。这称为并联回路发生 并联谐振（parrallel resonance）

由 $\omega_p C - \frac{1}{\omega_L L}=0$，可以推出谐振频率和谐振角频率（与串联谐振频率形式相同）：

\[\omega_p = \frac{1}{\sqrt{LC}}, \; f_p = \frac{1}{2\pi \sqrt{LC}}\]

此时的谐振电阻为 $R_p = \frac{L}{CR}$

我们定义品质因数 $Q_p$ 为（同串联）：

\[\begin{align} Q_p &= \frac{\omega_p L}{R} = \frac{1}{\omega_p C R} = \frac{1}{R} \sqrt{\frac{L}{C}} \\ &= \frac{R_p}{\omega_pL} = R_p \omega_p C = R_p \sqrt{\frac{C}{L}} \end{align}\]

我们由 $\omega_p C - \frac{1}{\omega_p L}=0$ 和 谐振电阻，可推导出：

\[\begin{align} R_p &= \frac{L}{CR} \\ &= \frac{\omega^2 L^2}{R} = Q_p \omega_P L\\ &= \frac{1}{R \omega_p^2 C^2} = Q_p \frac{1}{\omega_p C} \end{align}\]

上式说明，在谐振时，回路的谐振电阻等于 电感支路或电容支路电抗的 $Q_p$ 倍。

同时，各支路电流为：

\[\dot{I}_{Cp} = \dot{V}_0/\frac{1}{j \omega_p C} = \frac{L}{CR} \dot{I}_s \cdot j \omega_p C = j Q_p \dot{I}_s\\ \dot{I}_{Lp} = \dot{V}_0 / (R+j \omega_p L) \approx \frac{\dot{V}_0}{j \omega_p L} = \frac{L}{CR} \dot{I}_s\cdot \frac{1}{j\omega_p L} = - j Q_p \dot{I}_s\]

由上二式可见，并联谐振时，若 $\omega L \gg R$，则电容支路与电感支路的电流等大反相，相互抵消，此时总电流 $\dot{I}_s = \dot{I}_{Cp} + \dot{I}_{Lp}$

---

当不满足 $\omega L \gg R$ 时，有：

\[\begin{align} Z &= \frac{(R + j \omega L) \frac{1}{j\omega C} }{ R + j(\omega L - \frac{1}{\omega C})} \\ &= \frac{L}{CR} \frac{1 - j \frac{R}{\omega L}}{1 + j(\frac{\omega L}{R} - \frac{1}{\omega CR})} \end{align}\]

谐振时，要使上式为实数，即虚部为 0，所以有：

\[-\frac{R}{\omega_p L} = \frac{\omega_P L}{R} - \frac{1}{\omega_p C R}\\ \text{解得：} \omega_p = \sqrt{\frac{1}{LC} - \frac{R^2}{L^2}}\]

显然此时电阻并不为最大值

谐振曲线与通频带

当 $\omega L\gg R$ 时，

\[\frac{\dot{V}}{\dot{V}_0} = \frac{1}{1+jQ_p(\frac{\omega}{\omega_p}-\frac{\omega_p}{\omega})}\]

等式右边与串联的谐振曲线是一样的。所以我们不再讨论，直接给出结论：

1. 当 $\omega \rightarrow \omega_p$ 时，有：

   \[\frac{V}{V_0} \approx \frac{1}{\sqrt{1+\big( Q_p \frac{2\Delta\omega}{\omega_p} \big)^2}} = \frac{1}{\sqrt{1+\xi^2}}\\ \psi \approx -\arctan Q_p \frac{2\Delta\omega}{\omega_p} = -\arctan \xi\]

2. 绝对通频带为 $2 \Delta \omega_{0.7} = \frac{\omega_p}{Q_p}$

   相对通频带为 $\frac{2 \Delta \omega_{0.7}}{\omega_p} = \frac{1}{Q_p}$

3. 由 1、2 知，并联谐振的通频带、选择性与品质因数 $Q_p$ 的关系与串联相同

以上讨论的是高 $Q_p$（即 $\omega L \gg R$）的情况，低 $Q_p$ 的情况请自行推导。

内阻与负载的影响

考虑内阻和负载，则并联谐振回路的 Q 值为：

\[Q_L = \frac{Q_p}{\omega_p L (G_p + G_L + G_s)} = \frac{Q_p}{1+\frac{R_p}{R_s}+\frac{R_p}{R_L}}\]

低 Q 值并联回路

当 Q 低于 10 的电路都可叫做 低 Q 回路

\[Z = \frac{L}{CR} \frac{1 - j \frac{R}{\omega L}}{1 + j(\frac{\omega L}{R} - \frac{1}{\omega CR})}\]

当频率不变时，我们可以选择通过 调谐 $L$ 或调谐 $C$ 来获得谐振：

1. 若电阻集中在 $L$，则调谐 $C$ 可以使 $Z_p$ 为纯阻和 $Z_p$ 达到最大这两点重合；调谐 $L$ 不行
2. 反之，若电阻集中在 $C$，则调谐 $L$ 可以使 $Z_p$ 为纯阻和 $Z_p$ 达到最大这两点重合；调谐 $C$ 不行

考题

类型1 如何判断电路属于串联谐振还是并联谐振：

方法 串联谐振与并联谐振的根本区别在于：

1. 串联谐振：$Z = R + j X$ 可以为纯 $R$，即 $X=0, B=\infty$
2. 串联谐振：$Y = G + j B$ 可以为纯 $G$，即 $B=0, X=\infty$

一般，我们先列出 $Z$ 的表达式，分析其虚部 $jX$ 能否为 $0$ 或 $\infty$