放大器种的噪声可以分为:
- 内部噪声:自然/人为
- 外部噪声:自然/人为
下面主要讨论内部噪声
内部噪声

内部噪声一般是由的带电微粒无规则运动所产生,具有 起伏噪声(fluctuation noise)的性质,具有随机性,并且遵循一定的统计规律,所以我们可以用概率分布特性描述其噪声。
平均值
\[\bar{v}_n = \lim_{T\rightarrow\infty}\frac{1}{T} \int_0^T v_n(t) \dif t\]由于起伏噪声电压 $v_n(t)$ 是没有周期的,所以应该在较长时间内取平均值( $T\rightarrow\infty$)才有意义。
均方值(功率)
均方值(mean square value)用于表示噪声的起伏强度。起伏噪声电压的起伏强度为 $\Delta v_n(t)=v_n(t)-\bar{v}_n$,表示偏离均值的程度。由于强度有正有负,所以我们取其均方值:
\[\begin{align} \overline{\Delta v_n^2(t)}&=\overline{[v_n(t)-\bar{v}_n]^2}\\ &=\lim_{T\rightarrow\infty}\frac{1}{T} \int_0^T [\Delta v_n(t)]^2 \dif t\\ &= \lim_{T\rightarrow\infty}\frac{1}{T} \int_0^T [v_n(t)-\bar{v}_n]^2 \dif t\\ &= \overline{v_n^2}\quad(将 v_n(t) 平移\bar{v}_n) \end{align}\]为了将噪声与信号进行比较,我们也会取均方根值 $\sqrt{\overline{v_n^2}}$ 表示噪声电压交流分量的有效值,将其与信号电压作比,称为信号噪声比(信噪比 sign-noise ratio)
非周期噪声电压的频谱
起伏噪声可以看作是无数个时间 $\tau$ 极短的脉冲叠加,因此我们可以先研究单个脉冲。
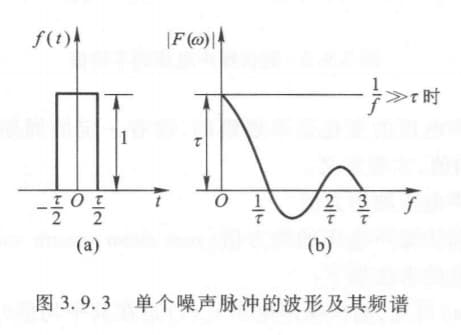
(这一部分需要信号与系统的相关基础)
起伏噪声的功率谱
已知,噪声功率的表达式:
\[\overline{v_n^2}=\lim_{T\rightarrow\infty}P=\lim_{T\rightarrow\infty}\frac{1}{T}\int_0^T v_n^2(t)\dif t\]若将 $P$ 拆分为不同频率信号的功率之和,则我们可以表示为:
\[P=\int_0^\infty S(f)\dif f\]式中,$S(f)$ 称为噪声功率谱密度,单位为 W/Hz。
实际设备中,只有在通频带 $\Delta f_n$ 内的噪声功率才能通过。
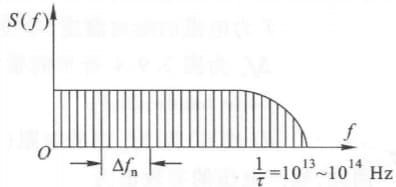
器件的噪声
电阻热噪声
自由电子做无规则变化产生噪声。由热运动理论和实践证明,有以下结论:
- 功率谱密度:$S(f)=4kTR$
- 噪声电压均方值:$\overline{v_n^2}=4kTR\Delta f_n$
- 噪声电流均方值:$\overline{i_n^2}=4kTG\Delta f_n$
其中,$k$是玻尔兹曼常数(Boltzmann constant≈1.38 × 10^-23 J/K),$T$ 为电阻的绝对温度,$\Delta f_n$ 为等效噪声带宽, $R、G$ 为电阻、电导。
噪声的表示与计算
噪声系数
信号噪声比 定义为信号与噪声的功率比 $P_s/P_n$
放大器的 噪声系数 $F_n$ 是指放大器 “输入端信噪比” 与 “输出端信噪比” 的比值:
\[F_n=\frac{P_{si}/P_{ni}}{P_{so}/P_{no}}\\ 或\\ F_n (\text{dB})=10\lg\frac{P_{si}/P_{ni}}{P_{so}/P_{no}}\]注意到 $P_{so}/P_{si}=A_p$,所以上式可以写成:
\[F_n=\frac{P_{no}}{P_{si}\cdot A_p}\]实际上,放大器的输出噪声 $P_{no}$ 由两部分组成:输入噪声的放大$P_{noⅠ}=P_{si}\cdot A_p$,以及 内部噪声 $P_{noⅡ}$,即:
\[P_{no}=P_{noⅠ}+P_{noⅡ}\]故噪声系数可表示为: \(F_n=\frac{P_{no}}{P_{si}\cdot A_p}=\frac{P_{no}}{P_{noⅠ}}=1+\frac{P_{noⅡ}}{P_{noⅠ}}\)
由于内部噪声是不可避免的,所以 $F_n>1$。从物理意义上看,噪声系数表示经过放大器后,信噪比变坏的程度。
噪声系数的另一种表示方法如下。我们知道,当负载与信号源内阻匹配时,有最大输出功率 $P’=\frac{V^2}{4 R}$,称为 额定功率(以后带 $’$ 的都是额定)。所以有:
\[P_{si}'=\frac{V_s^2}{4 R_s}\\ P_{ni}'=\frac{\overline{v_n^2}}{4R_s}=\frac{4kTR_s\Delta f_n}{4R_s}=kT\Delta f_n\]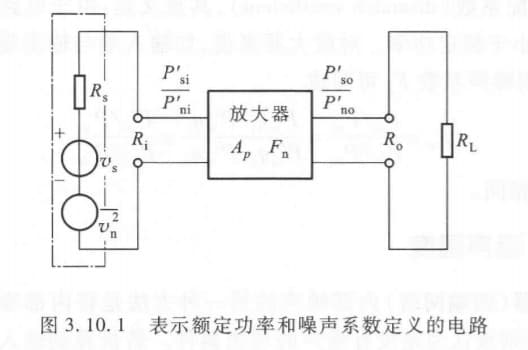
我们定义输入端、输出端均匹配时的功率增益为 $A_{pH}$,则:
\[F_n=\frac{P_{no}'}{P_{si}'\cdot A_{pH}}=\frac{P_{no}'}{kT\Delta f_n A_{pH}}\]顺便说一句,上式同样适用于非匹配情况。因为我们假设有 失配系数 $q_i, q_o$,则:
\[F_n=\frac{P_{si}/P_{ni}}{P_{so}/P_{no}}=\frac{P_{si}'q_i/P_{ni}'q_i}{P_{so}'q_o/P_{no}'q_o}=\frac{P_{si}'/P_{ni}'}{P_{so}'/P_{no}'}\]因此,我们下面都可以用额定功率来讨论。(顺便说一句,在实际中会有一定偏差)
噪声温度
若将放大器内部噪声折算到输入端,放大器本身认为是没噪声的理想元件,则总的输出端噪声功率为:
\[\begin{align} P_{no}'&=P_{no1}'+P_{no2}'\\ &= \left(P_{ni1}'+P_{ni2}'\right) A_{pH}\\ &=(kT\Delta f_n + kT_i\Delta f_n)A_{pH} \end{align}\]从而:
\[\begin{align} F_n&=1+\frac{P_{noⅡ}}{P_{noⅠ}}\\ &=1+\frac{A_{pH}kT_i\Delta f_n}{A_{pH}kT\Delta f_n}\\ &=1+\frac{T_i}{T} \end{align}\]$T_i$ 是一个假想的电阻的假想的温度,我们称之为 噪声温度,噪声温度可以表征放大器内部噪声的大小。
| Fn/dB | 0 | 0.3 | 0.5 | 1 | 2 | 4 | 8 | Ti/K | 0 | 20 | 35 | 76 | 171 | 443 | 1556 |
|---|---|---|---|---|---|---|---|
多级噪声系数
有一二级级联放大器,每一级的额定功率增益和噪声系数如图所示:
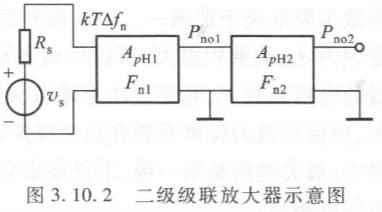
由:$F_n=\frac{P_{no}’}{P_{si}’\cdot A_{pH}}$ 可知:
\[P_{no1}'=kT\Delta f_n\cdot F_{n1}\cdot A_{pH1}\\\]而 $P_{no1}’$ 由两部分组成:输入噪声的放大 $kT\Delta f_n\cdot A_{pH1}$ 和自身产生的噪声 $P_{n1}$,由 $F_n=1+\frac{P_{noⅡ}}{P_{noⅠ}}$ 可知,自身产生的噪声为:
\[P_{n1}=(F_{n1}-1)\cdot kT\Delta f_n\cdot A_{pH1}\]同理,第二级输出噪声 $P_{no2}’$ 也包括两个部分:
\[P_{no2}'=P_{no1}'\cdot A_{pH2}+(F_{n2}-1)kT\Delta f_n A_{pH2}\]将第一级的输出噪声代入第二级:,有:
\[P_{no2}'=(kT\Delta f_n\cdot F_{n1}\cdot A_{pH1})\cdot A_{pH2}+(F_{n2}-1)kT\Delta f_n A_{pH2}\]根据公式 $F_n=\frac{P_{no}’}{P_{si}’\cdot A_{pH}}$,总的噪声系数为:
\[\begin{align} (F_n)_{1\cdot 2}&=\frac{P_{no2}'}{A_{pH}\cdot kT\Delta f_n}\\ &=\frac{(kT\Delta f_n\cdot F_{n1}\cdot A_{pH1})\cdot A_{pH2}+(F_{n2}-1)kT\Delta f_n A_{pH2}}{A_{pH1}A_{pH2}\cdot kT\Delta f_n}\\ &=F_{n1}+\frac{F_{n2}-1}{A_{pH1}} \end{align}\]我们可以递推出 n 级级联放大器的噪声系数为:
\[(F_n)_{1\cdot2\cdot\cdots\cdot n}=F_{n1}+\frac{F_{n2}-1}{A_{pH1}}+\frac{F_{n3}-1}{A_{pH1}A_{pH2}}+\cdots+\\ \frac{F_{nn}-1}{A_{pH1}A_{pH2}\cdots A_{pH(n-1)}}\]