预备知识
立体角
如果我们以某种锥体(例如圆锥,三棱锥,假设其无限高)的顶点 $O$ 作为圆心作一个半径为 1 的球(单位球),那么这个锥体的立体角(solid angle)就是单位球的表面被锥体截出的面积,通常用 $Ω$ 表示,单位为球面度(Sr).
半径为 $R$ 的球面的表面积为 $4\pi R^2$,所以立体角的取值范围是 $[0, 4\pi]$
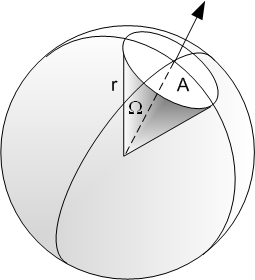
更一般的情况下,我们对在任一面 $S$ 上取 $\dif S$,则空间中任意点 $O$ 对 $\dif S$ 的立体角为:
\[\dif \Omega = \frac{\dif \vec{S}\cdot \vec{a}_R}{R^2}\]当 $O$ 在闭合面 $S$ 内时,$\Omega=\oint\frac{\dif \vec{S}\cdot \vec{a}_R}{R^2}=4\pi$;当 $O$ 在闭合面 $S$ 外时,由于必存在一对等值异号的 $\dif \Omega$,所以 $\Omega=0$
高斯定理
已知点电荷在真空中的电场为:
\[\vec{E} = \frac{q}{4\pi\varepsilon_0} \frac{\vec{a}_R}{R^2}\]我们任意作一个封闭面 $S$,则 $E$ 穿出 $S$ 的通量为:
\[\oint_S \vec{E}\cdot\dif \vec{S} = \frac{q}{4\pi\varepsilon_0} \oint_S \frac{\vec{a}_R}{R^2}\cdot\dif\vec{S}=\frac{q}{4\pi\varepsilon_0}\oint_S \dif \Omega\\ =\begin{cases} q/\varepsilon_0 & q在S内\\ 0 & q在S外 \end{cases}\]从而:
\[\begin{align} \oint_S \vec{E}\cdot\dif\vec{S}&=\frac{\sum q}{\varepsilon_0}\\ &\Downarrow\\ \int_V \nabla\cdot\vec{E}\dif V&=\frac{1}{\varepsilon_0}\int_V\rho\dif V\\ &\Downarrow\\ \nabla\cdot\vec{E}&=\rho/\varepsilon_0 \end{align}\]以上式子即高斯公式的积分形式与微分形式。
我们也可以用电位移矢量 $\vec{D}=\varepsilon_0\vec{E}$ 来代替 $\vec{E}$,从而得到高斯定理的另一种形式:
\[\oint_S \vec{D}\cdot\dif \vec{S} \oint_S \varepsilon_0\vec{E}\cdot\dif \vec{S}=Q\\ \nabla\cdot\vec{D}=\rho\]电场的旋度
体密度为 $\rho(\vec{r}’)$ 的电荷产生的电场强度为:
\[\vec{E}(\vec{r})=-\frac{1}{4\pi\varepsilon_0}\int_{V'} \rho(\vec{r}') \nabla (\frac{1}{R})\dif V'\]注意到,积分的对象是 $(x’,y’,z’)$ 处的电荷,而梯度 $\nabla$ 的对象是 $(x,y,z)$,两个运算对象不同,所以可以交换次序:
\[\vec{E}(\vec{r})=- \nabla \left[ \frac{1}{4\pi\varepsilon_0}\int_{V'} \rho(\vec{r}')\frac{1}{R}\dif V' \right]\]根据梯旋散公式,可知:
\[\nabla\times\vec{E}(\vec{r}) = \nabla\times \left\{ - \nabla \left[ \frac{1}{4\pi\varepsilon_0}\int_{V'} \rho(\vec{r}')\frac{1}{R}\dif V' \right] \right\} \equiv 0\]因此静电场是一个无旋场。根据斯托克斯公式:
\[\oint_c\vec{E}\cdot\dif \vec{l} =\int_S \nabla\times\vec{E}\cdot\dif\vec{S}=\int_S \vec{0}\cdot\dif \vec{S}=0\]说明静电场沿闭合路径的积分(环量)为 0,从而积分与路径无关。
值得注意的是,$\int_c\vec{E}\cdot\dif \vec{l}$ 的物理意义是电场力对单位正电荷所做的功。因为这个积分与路径无关,所以只要确定两点,就能求出功,故定义电压:
\[U_{PQ}=\int_P^Q \vec{E}\cdot\dif\vec{l}\]例题:求点电荷 $q$ 电场中,$PQ$ 之间的电压?
答案
$$ U_{PQ}=\int_P^Q\vec{E}\cdot\dif\vec{l}=\int_P^Q \frac{q}{4\pi\varepsilon_0} \frac{\vec{a}_R}{R^2}\cdot\dif\vec{l}\\ 球坐标系:\dif\vec{l}=\vec{a}_R \dif R+\vec{a}_\theta R\dif\theta + \vec{a}_\varphi R\sin\theta\dif\varphi\\ 故:U_{PQ}=\frac{q}{4\pi\varepsilon_0} \int_P^Q \frac{\dif R}{R^2}=\frac{q}{4\pi\varepsilon_0}\left( \frac{1}{R_P}-\frac{1}{R_Q} \right) $$请做完上面那道例题后,对比一下:
\[\frac{1}{4\pi\varepsilon_0}\int_{V'} \rho(\vec{r}')\frac{1}{R}\dif V' \Leftrightarrow \frac{q}{4\pi\varepsilon_0}\left( \frac{1}{R_P}-\frac{1}{R_Q} \right)\]左边是交换次序后得到的式子,而右边则是点电荷中的电压。可以看出左边式子就是“电势”(电位),右边式子是“电势差”。
我们将在下一节中进一步学习。
总结
电场的表示: \(\nabla\cdot\vec{D}=\rho\\ \nabla\times\vec{E}=0\\ \vec{D}=\varepsilon_0\vec{E}\)