静电场中的导体
导体中含有自由电子,在电场作用下,电荷重新分布,直到电荷产生的附加电场与外加电场相互抵消为止。此时,导体内的电荷不再做宏观的移动,此时称为静电平衡,此时的导体就有如下性质:
- 导体内的电场强度应为 0(否则电荷会移动,就不是静电平衡)
- 导体是一个等位体,其表面是等位面(电场强度为0)
- 电场强度方向与导体表面垂直(导体表面是等位面)
- 若导体本身带有净电荷,则这些电荷必定分布于导体表面(否则不满足 1.)
电介质
电偶极子
两个距离很近的等值异号电荷称为电偶极子
考虑在空间中一点 $P$ 的电位。根据电电荷的电位公式:
\[\phi=\frac{q}{4\pi\varepsilon_0}(\frac{1}{r_1}-\frac{1}{r_2})\\ =\frac{q}{4\pi\varepsilon}\frac{r_2-r_1}{r_1 r_2}\]当 $P$ 电较远时,即 $r«d$ 时,有:
\[r_2-r_1\approx l\cos\theta\\ r_1r_2\approx r^2\]于是有:
\[\phi=\frac{ql\cos\theta}{4\pi\varepsilon_0 r^2}=\frac{\vec{p}\cdot\vec{r}}{4\pi\varepsilon_0 r^3}\]$\vec{p}=q\vec{l}$ 称为电偶极子的电偶极距,其方向由 -q 指向 +q.
本来矢径应该用 $R$ 的,但是为了和图保持统一,故用 $r$
有极分子/无极分子
分子有两类:有极分子与无极分子,其区别在于分子内部正负电荷的作用中心是否重合。
 |
 |
|---|
在外电场的作用下,电介质发生极化:
- 无极分子的正负电荷中心发生相对位移,形成与外电场方向一致的电偶极子。称为位移极化;
- 有极分子发生转动,使得方向与外电场方向一致。称为转向极化;
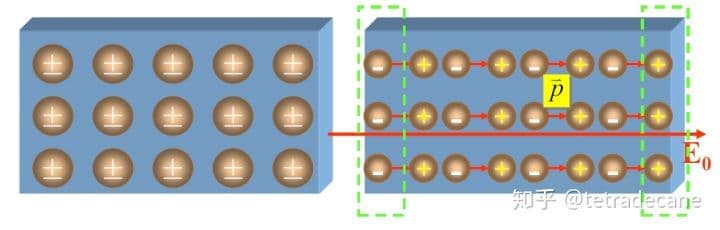
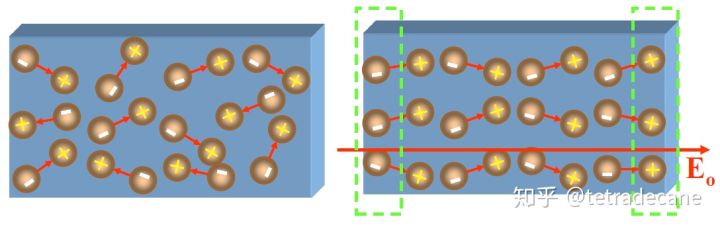
极化后产生的电荷称为极化电荷,也叫束缚电荷。极化电荷只能抵消部分外电场,无法将其消除。为了计算场强,我们定义极化强度为单位体积内的电偶极距:
\[\vec{P}=\lim_{\Delta V\rightarrow0}\frac{\sum_i \vec{p}_i}{\Delta V} \;\text{单位 C/m^2}\]那么体积元内的电偶极子 $\dif \vec{p}=\vec{P}\dif V’$ 的电位为:
\[\dif \phi =\frac{1}{4\pi\varepsilon_0} \frac{\dif \vec{p}\cdot\vec{R}}{R^3}=\frac{\dif V'}{4\pi\varepsilon_0}\vec{P}\cdot \left( \nabla'\frac{1}{R} \right)\\ \phi(\vec{r}) =\int \dif \phi = \frac{1}{4\pi\varepsilon_0} \int_V \vec{P} \cdot \left( \nabla'\frac{1}{R} \right)\dif V'\]由矢量恒等式 $\vec{P}\cdot\left( \nabla’\frac{1}{R} \right) = \nabla’\left(\vec{P}\cdot\frac{1}{R} \right)-\frac{1}{R} \nabla’\cdot\vec{P}$,我们有:
\[\begin{align} \phi(\vec{r})&= \frac{1}{4\pi\varepsilon_0} \int_V \left[\nabla'\left(\vec{P}\cdot\frac{1}{R} \right)-\frac{1}{R} \nabla'\cdot\vec{P} \right] \dif V'\\ 高斯定理:&=\frac{1}{4\pi\varepsilon_0} \oint_S \frac{\vec{P}\cdot\dif \vec{S}'}{R}+\frac{1}{4\pi\varepsilon_0} \int_V\frac{-\nabla'\cdot\vec{P}}{R}\dif V' \end{align}\]我们对比真空中的电位公式:$\phi =\frac{1}{4\pi\varepsilon_0} \int \frac{\rho(r’)}{R}$ 可以看出,等号右边的两部分分别是极化电荷的等效面密度与等效体密度。即:
\[\rho_{sp}=\vec{P}\cdot\vec{n}\\ \rho_{p}=-\nabla'\cdot \vec{P}=-\nabla\cdot \vec{P}\]各向同性/异性的电介质
实验结果表明,若电介质极化强度 $\vec{P}$ 与外加电场强度 $\vec{E}$ 有如下关系:
\[\vec{P}=\chi_\varepsilon \varepsilon_0 \vec{E}\]则称为各向同性的电介质,即无论外加电场方向,其极化强度的数值都相同。反之,若不同方向的极化强度值不同,则称为 各向异性的电介质。