\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}\\
\newcommand{\p}{\partial}\\
\newcommand{\bd}{\boldsymbol}\\
\newcommand{\db}[1]{\dot{\boldsymbol{#1}}}\\
\newcommand{\E}{\mathscr{E}}
\end{align*}\]
前情回顾:
-
在时变电磁场中,电磁场的能量密度为:
\[w=w_e+w_m\\ =\frac{1}{2}\bd{D}\cdot\bd{E}+\frac{1}{2}\bd{H}\cdot\bd{B}\\ =\frac{1}{2}\varepsilon E^2 + \frac{1}{2}\mu H^2\] -
损耗功率密度为:
\[p=\bd{J}\cdot \bd{E}=\sigma E^2\]
时域坡印廷定理
\[\begin{align} \nabla\cdot (\bd{E}\times\bd{H})&=\bd{H}\cdot(\nabla \times \bd{E})- \bd{E}\cdot(\nabla \times\bd{H})\\ &=\bd{H}\cdot(-\frac{\p \bd{B}}{\p t})-\bd{E}\cdot(\bd{J}_c + \frac{\p \bd{D}}{\p t})\\ &=-\bd{H} \cdot \frac{\p \bd{B}}{\p t} - \bd{E} \cdot \frac{\p\bd{D}}{\p t}-\bd{J}_c \cdot \bd{E}\\ &=-\frac{\p}{\p t} (\frac{1}{2} \bd{B}\cdot\bd{H})-\frac{\p}{\p t} (\frac{1}{2} \bd{E} \cdot \bd{D})-\bd{J}_c \cdot \bd{E}\\ &=-\frac{\p w_m}{\p t}-\frac{\p w_e}{\p t}-\bd{J}_c \cdot \bd{E} \end{align}\]对上式两边取体积分,并根据散度定理对左边化简:
\[-\oint_S \bd{E}\times\bd{H} \cdot \dif \bd{S}=\frac{\p}{\p t}\int_\tau (w_m+w_e)\dif \tau + \int_\tau \sigma E^2\dif \tau\]注意到右边分别是电场能量、磁场能量、介质损耗,则左边就是波的能量。上式就是 坡印廷定理(能流定理)
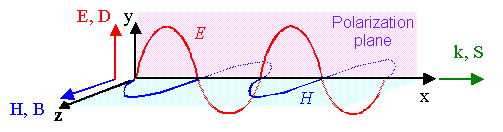
为了描述能量流动的情况,引入坡印廷矢量 $\bd{S}$(看作功率密度)
\[\bd{S}(t)=\bd{E}(t)\times\bd{H}(t) \quad \rm{W/m^2}\]表示单位时间内垂直穿过单位面积的能量(瞬时值),表示能量流动的大小和方向。
下面分析能速。考虑在完纯介质($\sigma=0$)中的坡印廷定理:
\[-\oint_S \bd{S} \cdot \dif \bd{S}=\frac{\p}{\p t}\int_\tau (w_m+w_e)\dif \tau\\ \nabla\cdot \bd{S}=-\frac{\p (w_e+w_m)}{\p t}\]我们知道,电流密度有如下关系:
\[\nabla\cdot\bd{J}=-\frac{\p \rho}{\p t}\\ \bd{J}=\rho \bd{v}\]类比可知,电磁能的流动速度为:
\[\bd{v}=\frac{\bd{S}(t)}{w_e+w_m}\]坡印廷矢量的周期平均值:$\bd{S}_\mathrm{av}=\frac{1}{T}\int_0^T \bd{S}\dif t$
对于时谐场:
\[\bd{E}(\bd{r},t)=\bd{E}_m(\bd{r}) \cos[\omega t+ \phi_E(\bd{r})]\\ \bd{H}(\bd{r},t)=\bd{H}_m(\bd{r}) \cos[\omega t+ \phi_H(\bd{r})]\]则:
\[\begin{align} \bd{S}_{av}&=\frac{1}{T}\int_0^T \bd{E}_m(\bd{r}) \cos[\omega t+ \phi_E(\bd{r})] \times \bd{H}_m(\bd{r}) \cos[\omega t+ \phi_H(\bd{r})] \dif t\\ &=\frac{1}{2} \bd{E}_m \times \bd{E}_m(\bd{r})\cos(\phi_E-\phi_H) \end{align}\]复坡印廷矢量
能量密度(最大值):
\[\begin{cases} w_{e\max}=\dfrac{1}{2}\varepsilon E_m^2(\bd{r})=\dfrac{1}{2}\varepsilon \db{E}_m\cdot\db{E}_m^*\\ w_{m\max}=\dfrac{1}{2}\mu H_m^2(\bd{r})=\dfrac{1}{2}\mu \db{H}_m\cdot\db{H}_m^* \end{cases}\]定义复坡印廷矢量:
\[\begin{align} \db{S}&=\frac{1}{2} \db{E}_m \times \db{H}_m^*\\ &=\frac{1}{2} [\bd{E}_m(\bd{r})\times \bd{H}_m(\bd{r}) e^{j(\phi_E-\phi_H)}]\\ \bd{S}_{av}&=\mathrm{Re} [\frac{1}{2} \db{E}_m \times \db{H}_m] \end{align}\]可以看出,复坡印廷矢量的实部表示能量的流动;虚部则表示能量交换。故有以下三类情况:
- $\phi_E-\phi_H=k\pi$,波流动
- $\phi_E-\phi_H=(2n+1)\frac{\pi}{2}$ 波能量交换
- 其他,波既流动又有能量交换
频域坡印廷定理
我们的过程和上面类似:
\[\nabla\cdot(\db{E}\times\db{H}^*)=\db{H}^*\cdot(\nabla\times\db{E})-\db{E}\cdot(\nabla\times\db{H}^*)\\ 其中, \begin{cases} \nabla\times\db{E}=-j\omega\mu\db{H}\\ \nabla\times\db{H}^*=\sigma \db{E}^*-j\omega \varepsilon^*\db{E}^*=-j\omega \varepsilon_c \end{cases}\\ 从而:\\ -\oint_S \frac{1}{2} \db{E}\times \db{H}^* \cdot \dif \bd{S} = j\omega \int_\tau(\frac{1}{2} \mu H^2-\frac{1}{2}\varepsilon^* E^2)\dif \tau + \int_\tau \frac{1}{2}\sigma E^2 \dif \tau\]若无滞后效应,$\mu,\varepsilon$ 为实数,则:
\[-\oint_S \frac{1}{2} \db{E}\times \db{H}^* \cdot \dif \bd{S} = j\omega \int_\tau(\frac{1}{2} \mu H^2-\frac{1}{2}\varepsilon E^2)\dif \tau + \int_\tau \frac{1}{2}\sigma E^2 \dif \tau\]若有滞后效应,$\mu,\varepsilon$ 为复数,则:
\[\frac{1}{2} j \omega \mu H^2=\frac{1}{2} j \omega (\mu' -j\mu'') H^2 = \frac{1}{2} \omega \mu'' H^2 + \frac{1}{2} j\omega \mu' H^2\\ -\frac{1}{2} j \omega \varepsilon^* E^2=\frac{1}{2} j \omega (\varepsilon' +j\varepsilon'') E^2 = \frac{1}{2} \omega \varepsilon'' E^2 - \frac{1}{2} j\omega \varepsilon' E^2\] \[\begin{align} -\oint_S \frac{1}{2} \db{E}\times \db{H}^* \cdot \dif \bd{S} &= \int_\tau(\frac{1}{2} \sigma E^2 + \frac{1}{2} \omega \mu'' H^2 + \frac{1}{2}\omega\varepsilon'' E^2)\dif \tau & 实部\\ &+ j\int_\tau \omega \frac{1}{2} \omega (\mu' H^2 - \frac{1}{2}\varepsilon' E^2) \dif \tau & 虚部\\ &=\int_\tau (p_T+p_m+p_e)\dif \tau + j \int_\tau 2\omega (\overline{w}_m - \overline{w}_e) \end{align}\]实部为 $p_T$ 热损耗 + $p_m$ 磁损耗 + $p_e$ 介电损耗;虚部为电场能量与磁场能量的交换。