\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}\\
\newcommand{\p}{\partial}\\
\newcommand{\bd}{\boldsymbol}\\
\newcommand{\E}{\mathscr{E}}
\end{align*}\]
由于麦克思维方程组的微分形式在不同媒质的分界面上不成立（不连续），所以只能用积分形式来推导。
\[\begin{cases} \oint_C \bd{H}\cdot\dif\bd{l}=\int_S \bd{J}\cdot \dif \bd{S}+\int_S \frac{\p \bd{D}}{\p t} \cdot \dif \bd{S}\\ \oint_C \bd{E}\cdot\dif\bd{l}=-\int_S \frac{\p \bd{E}}{\p t} \cdot \dif \bd{S}\\ \oint_S \bd{B} \cdot \dif \bd{S} = 0\\ \oint_S \bd{D}\cdot \dif \bd{S}=q \end{cases}\]法向边界条件
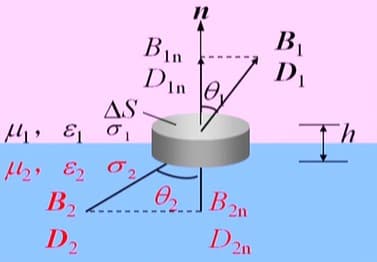
作闭合柱面，根据前面的过程（这里就不写了），我们有：
\[\begin{cases} \bd{n} \cdot (\bd{B}_1-\bd{B}_2)=0\\ \bd{n}\cdot (\bd{D}_1-\bd{D}_2)=\rho_s\\ \end{cases} 或 \begin{cases} B_{1n}=B_{2n}\\ D_{1n}-D_{2n}=\rho_s\\ \end{cases}\]切向边界条件
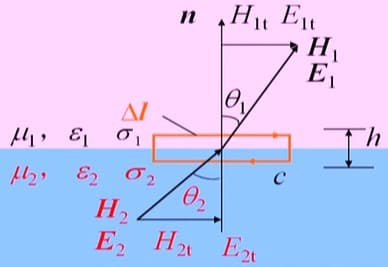
作闭合矩形，根据前面的过程（这里就不写了），我们有：
\[\begin{cases} \bd{n} \times (\bd{H}_1-\bd{H}_2)=\bd{J}_s\\ \bd{n}\times (\bd{E}_1-\bd{E}_2)=0\\ \end{cases} 或 \begin{cases} H_{1t}-H_{2t}=J_s\\ E_{1t}-E_{2t}=0\\ \end{cases}\]下面对切向磁场进行解释（为什么没有传导电流）。
对磁场进行线积分，有：
\[\oint_C \bd{H} \cdot \dif \bd{l}=\bd{H}_1 \cdot \hat{t}\Delta l- \bd{H}_2 \cdot \hat{t} \Delta l=I_C+I_D\\ \begin{align*} I_C&=\int_S \bd{J}\cdot\dif \bd{S}=\bd{J}_S\cdot\hat{a}_S \Delta l\\ I_D&=\int_S \frac{\p \bd{D}}{\p t} \cdot \dif S=\lim_{\Delta h\rightarrow 0} \frac{\p \bd{D}}{\p t}\cdot \hat{a}_S \Delta h \Delta l=0 \end{align*}\\ \therefore \hat{n}\times(\bd{H}_1-\bd{H}_2)=\bd{J}_S\]总结
总结如下：切向电场强度与法向磁感应强度连续，法向电位移和切向磁场强度不连续。
\[\begin{cases} H_{1t}-H_{2t}=J_s\\ E_{1t}-E_{2t}=0\\ B_{1n}-B_{2n}=0\\ D_{1n}-D_{2n}=\rho_s \end{cases}\\ （从2指向1）\]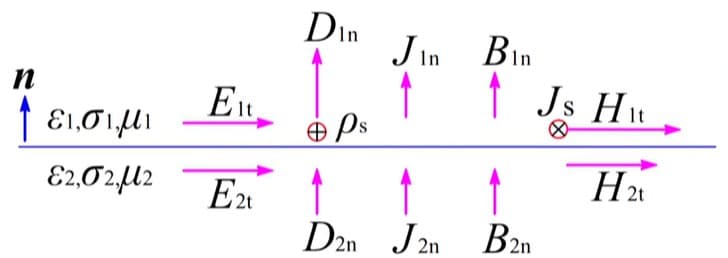
理想媒质的边界条件
对于理想导体（$\sigma\rightarrow\infty$），$\bd{E}=0$，$\bd{B}=0$。我们把导体看作媒质2，则有：
\[\begin{cases} \hat{n}\times\bd{H}_1=\bd{J}_S\\ \hat{n}\times \bd{E}_1=0\\ \hat{n}\cdot \bd{B}_1=0\\ \hat{n}\cdot \bd{D}_1=\rho_S \end{cases}\]上式说明：
- 理想导体表面切向电场和法向磁场为零；
- 电场总垂直于导体表面，磁场从平行于导体表面
- 理想导体内不能存在电磁场
（例 5-2-1）
波动方程
在物理种，场量 $u$ 的波动方程标准形式为：
\[\nabla^2 u -\frac{1}{v^2} \frac{\p^2 u}{\p t^2}=-g\]$v$ 是波速，$t$ 是时间，$g$ 是源。波动方程的解为以速度 $v$ 传播的波。我们下面要做的，就是用麦克斯韦方程组，导出类似形式的电磁场波动方程：
无源区的波动方程
在均匀、各向同性的媒质种，麦克斯韦方程组为：
\[\begin{cases} \nabla\times\bd{H}=\varepsilon \frac{\p \bd{E}}{\p t}\\ \nabla\times\bd{E}=-\mu\frac{\p\bd{H}}{\p t}\\ \mu \nabla \cdot \bd{H}=0\\ \varepsilon \nabla \cdot \bd{E}=0 \end{cases}\]对第二方程求旋度：
\[\nabla\times\nabla\times\bd{E}=-\mu\nabla\times \frac{\p \bd{H}}{\p t}\\ \because \nabla\times\nabla\times\bd{E}=\nabla(\nabla\cdot \bd{E})-\nabla^2 \bd{E}\\ \therefore \nabla(\nabla\cdot \bd{E})-\nabla^2 \bd{E}=-\mu \frac{\p}{\p t} \nabla\times \bd{H}\]代入第一、四方程，得到：
\[\nabla^2 \bd{E}-\mu\varepsilon \frac{\p^2\bd{E}}{\p t^2}=0\]同样可以推出：
\[\nabla^2 \bd{H}-\mu\varepsilon \frac{\p^2\bd{H}}{\p t^2}=0\]在直角坐标系中，拉普拉斯算符可以分解为三个方向的拉普拉斯算符之和，即：
\[\nabla^2 E_x-\mu\varepsilon \frac{\p^2 E_x}{\p t^2}=0\\ \nabla^2 E_y-\mu\varepsilon \frac{\p^2 E_y}{\p t^2}=0\\ \nabla^2 E_z-\mu\varepsilon \frac{\p^2 E_z}{\p t^2}=0\]而标量的拉普拉斯算符为：
\[\nabla^2=\frac{\p^2}{\p x^2}+\frac{\p^2}{\p y^2}+\frac{\p^2}{\p z^2}\]故有：
\[\frac{\p^2 E_x}{\p x^2}+\frac{\p^2 E_x}{\p y^2}+\frac{\p^2 E_x}{\p z^2}-\mu\varepsilon \frac{\p^2 E_x}{\p t^2}=0\]有源区的波动方程
设媒质均匀、线性、各向同性，对麦克斯韦方程组的第一、第二方程求导数：
\[\begin{align} \nabla\times\nabla\times\bd{H}&=\nabla\times\bd{J}+\nabla\times\frac{\p\bd{D}}{\p t}\\ &=\nabla\times\bd{J}+\frac{\p \nabla\times\bd{D}}{\p t}\\ &=\nabla\times\bd{J}+\varepsilon \frac{\p \nabla\times\bd{E}}{\p t}\\ &=\nabla\times\bd{J}+\varepsilon\frac{\p\bd{B}}{\p t} \\ &=\nabla\times\bd{J}+\varepsilon\mu \frac{\p\bd{H}}{\p t} \end{align}\]而 $\nabla\times\nabla\bd{F}=\nabla(\nabla\cdot\bd{F})-\nabla^2 \bd{F}$
所以：
\[\begin{cases} \nabla^2 \bd{H}-\mu\varepsilon \frac{\p^2 \bd{H}}{\p t^2}=-\nabla\times\bd{J} \end{cases}\]电磁波的一般概念
为了方便运算，我们假设 $\bd{E}=\hat{a}_x E_x(z,t)$，那么由波动方程：
\[\nabla^2 E_x-\mu\varepsilon \frac{\p^2 E_x}{\p t^2}=0\\ \frac{\p^2 E_x}{\p z^2}-\mu\varepsilon \frac{\p^2 E_x}{\p t^2}=0\]这个方程有点复杂，这里直接给出其解的形式：
\[E_x(z,t)=f(t-\frac{z}{v})+g(t+\frac{z}{v})\\ =A\cos \omega(t-\frac{z}{v})+B \cos \omega(t+\frac{z}{v})\\ v=\frac{1}{\sqrt{\mu\varepsilon}} \quad \rm{m/s}\]式中 $f,g$ 是三角函数。先分析 $f$，选定相同相位点：
\[\varphi_0=t_1-\frac{z_1}{v}=t_2-\frac{z_2}{v}\]假如 $t_1 < t_2$，则 $z_1 < z_2$，也就是说，当时间推移时，电磁波 $f$ 向 $+z$ 方向传播。此时，$z_2-z_1=v(t_2-t_1)$，说明传播速度就是 $v$。我们称 $f$ 为入射波（顺行波）。
类似地，电磁波 $g$ 向 $-z$ 方向传播，我们称 $g$ 为反射波（逆行波）。
在真空中，$v=c$