\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}\\
\newcommand{\p}{\partial}\\
\newcommand{\bd}{\boldsymbol}
\end{align*}\]
镜像法
- 实质:用一个或多个等效电荷代替边界的影响,将原来具有边界的非均匀空间变成无限大的均匀自由空间,从而简化计算。
- 依据:唯一性定理。等效电荷的引入必须维持原来的边界条件不变,故原来区域中的静电场没有改变。
- 局限性:仅适用于特殊的边界和特殊分布的电荷。
- 关键:确定镜像电荷的大小及其位置。
导体平面的镜像
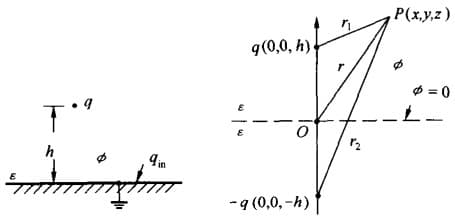
点电荷对无限大接地导体平面的镜像

设无限大 接地 导体平面上 $h$ 处有一点电荷 $q$,其周围是介电常数为 $\varepsilon$ 的介质。其边界条件为:
\[\begin{cases} \nabla^2 \phi=0 & (z > 0 除了电荷处)\\ \phi=0 & (z=0) \end{cases}\]我们可以用一个 $-q$ 代替原有的导体上的感应电荷,从而将无穷大导体平面撤去。此时,$z\geq0$ 区域的场不变,故有:
\[\begin{align} \phi&=\frac{q}{4\pi \varepsilon} \left( \frac{1}{r_1}-\frac{1}{r_2} \right)\\ &=\frac{q}{4\pi\varepsilon} \left( \frac{1}{[x^2+y^2+(z-h)^2]^{1/2}}-\frac{1}{[x^2+y^2+(z+h)^2]^{1/2}}\right) \end{align}\]因为 $\nabla^2 (\frac{1}{r})=0$(关于这个的讨论:On the Laplacian of 1/r),我们可以简单地写一下证明:
\[\begin{align} \nabla^2 \left( \frac{1}{r} \right) &= \left( \frac{\p^2 }{\p x^2}+\frac{\p^2 }{\p y^2}+\frac{\p^2 }{\p z^2} \right) \frac{1}{\sqrt{x^2+y^2+z^2}}\\ \frac{\p}{\p x} \frac{1}{\sqrt{x^2+y^2+z^2}} &= -\frac{x}{(x^2+y^2+z^2)^{3/2}}\\ \frac{\p}{\p x} \frac{x}{(x^2+y^2+z^2)^{3/2}} &=\frac{(x^2+y^2+z^2)^{3/2}-3x^2(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^3}\\ &=\frac{(x^2+y^2+z^2)^{1/2}[(x^2+y^2+z^2)-3x^2]}{(x^2+y^2+z^2)^3}\\ \therefore \nabla^2 \left( \frac{1}{r} \right) &= 0 \end{align}\]所以,$\nabla^2 \phi=0$,$(r_1\neq0)$,满足原有的条件。