\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}\\
\newcommand{\p}{\partial}\\
\newcommand{\bd}{\boldsymbol}
\end{align*}\]
$$ \begin{cases} \dif \bd{l}'=\dif \bd{z}'\\ z'=z-\frac{r}{\tan\theta}\\ \dif z'= r\csc^2 \theta\dif \theta\\ \dif \bd{z}'=\bd{a}_z r\csc^2 \theta\dif \theta\\ \bd{a}_R=\bd{a}_r \sin\theta+\bd{a}_z\cos\theta\\ \dif z'\times \bd{a}_R=\bd{a}_\varphi r \csc^2\theta\sin\theta \dif \theta\\ R=r\csc\theta \end{cases} $$ 将上面最后两项代入比奥-萨伐尔定律:
$$ \begin{align} \bd{B}&=\frac{\mu_0}{4\pi}\int_{c'} \frac{I\dif \bd{l}'\times \bd{a}_R}{R^2}\\ &=\frac{\mu_0 I}{4\pi} \int_{\theta_1}^{\theta_2} \frac{r\csc^2\theta\sin\theta\dif \theta}{r^2\csc^2 \theta}\\ &=\frac{\mu_0 I}{4\pi r} \int_{\theta_1}^{\theta_2} \sin\theta\dif\theta\\ &=\frac{\mu_0 I}{4\pi r} (\cos\theta_1 - \cos \theta_2) \end{align} $$ 由上可以推出无限长直导线的磁场强度为 $\bd{B}=\frac{\mu_0 I}{2\pi r} \bd{a}_\varphi$
恒定电流产生的磁场就是恒定磁场,磁铁的磁场是由分子环流所产生的,所以也属于恒定磁场。
磁感应强度
安培力定律
安培经实验证明,通电回路之间有相互作用力。真空中,两个电流元之间的作用力为:
\[\dif \bd{F}_{21}=\frac{\mu_0}{4\pi}\frac{I_2\dif \bd{l}_2 \ \times I_1\dif \bd{I}_1}{R_{21}^3}\times \bd{R}_{21}\]式中,$\mu_0=4\pi\times 10^{-7} \rm{H/m}$ 为真空中的磁导率。
所以两个电流回路间的作用力为:
\[\bd{F}_{21}=\frac{\mu_0}{4\pi}\oint_{c_2}{\oint_{c_1}} \frac{I_2\dif \bd{l}_2 \times I_1 \dif \bd{l}_1 \times \bd{a}_R}{R^2}\]比奥-萨伐尔定律
将安培力改写为
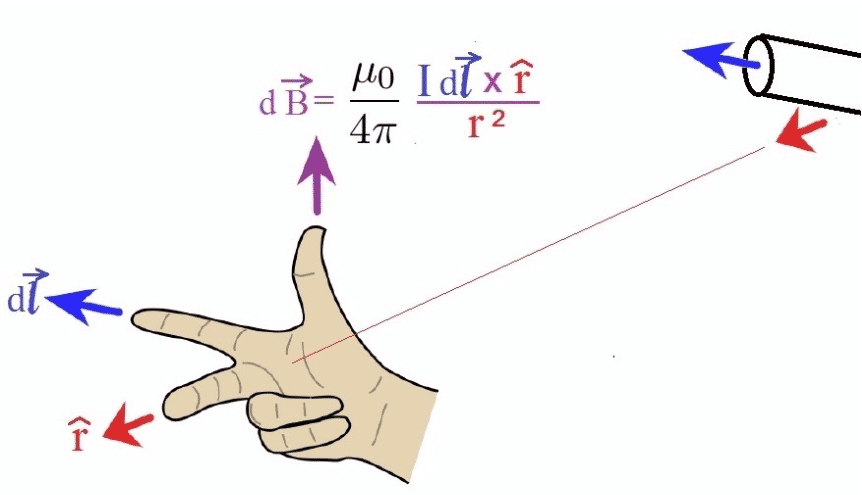
\[\bd{F}_{21}=\oint_{c_2} I_2\dif \bd{l}_2 \times \left( \frac{\mu_0}{4\pi}{\oint_{c_1}} \frac{ I_1 \dif \bd{l}_1 \times \bd{a}_R}{R^2} \right)\]括号中就是回路 $c_1$ 在空间中产生的磁场,我们称之为 磁感应强度,磁感应强度满足右手定则,即:

上式即 比奥-萨伐尔定律(Biot-Savert),这是实验定律。磁感应强度的单位是 $1\rm{T}=10^4 \rm{Gs}$ 或 $\rm{Wb/m^2}$
我们也可以用电流密度来表示:
\[体电流 \bd{B}(\bd{r})=\frac{\mu_0}{4\pi}{\int_{V'}} \frac{ \bd{J}(\bd{r}') \times \bd{a}_R}{R^2}\dif V'\\ 面电流 \bd{B}(\bd{r})=\frac{\mu_0}{4\pi}{\oint_{S'}} \frac{ \bd{J}_S(\bd{r}') \times \bd{a}_R}{R^2}\dif S'\\ 线电流直接用电流表示即可\]可以看出磁感应强度比电场强度更复杂(因为有更多的矢量运算),所以后面我们引入的位函数也会更复杂。
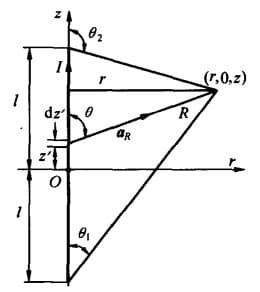
例题:一段长为 $2l$ 的直导线通流 $I$,求空间各点的磁感应强度。
解:以导线中点为原点,导线为 $z$ 轴,建立柱坐标系:

$$ \begin{cases} \dif \bd{l}'=\dif \bd{z}'\\ z'=z-\frac{r}{\tan\theta}\\ \dif z'= r\csc^2 \theta\dif \theta\\ \dif \bd{z}'=\bd{a}_z r\csc^2 \theta\dif \theta\\ \bd{a}_R=\bd{a}_r \sin\theta+\bd{a}_z\cos\theta\\ \dif z'\times \bd{a}_R=\bd{a}_\varphi r \csc^2\theta\sin\theta \dif \theta\\ R=r\csc\theta \end{cases} $$ 将上面最后两项代入比奥-萨伐尔定律:
$$ \begin{align} \bd{B}&=\frac{\mu_0}{4\pi}\int_{c'} \frac{I\dif \bd{l}'\times \bd{a}_R}{R^2}\\ &=\frac{\mu_0 I}{4\pi} \int_{\theta_1}^{\theta_2} \frac{r\csc^2\theta\sin\theta\dif \theta}{r^2\csc^2 \theta}\\ &=\frac{\mu_0 I}{4\pi r} \int_{\theta_1}^{\theta_2} \sin\theta\dif\theta\\ &=\frac{\mu_0 I}{4\pi r} (\cos\theta_1 - \cos \theta_2) \end{align} $$ 由上可以推出无限长直导线的磁场强度为 $\bd{B}=\frac{\mu_0 I}{2\pi r} \bd{a}_\varphi$
洛伦兹力
由安培力表达式推出:
\[\begin{align*} \dif \bd{F} &= I\dif \bd{I}\times\bd{B}=\bd{J}\dif V\times\bd{B}=\rho \bd{v} \dif V \times \bd{B}\\ &=\dif q \bd{v}\times \bd{B} \end{align*}\]所以,磁场对运动电荷的作用力为:
\[洛伦兹力\;\bd{F}=q\bd{v}\times\bd{B}\]