\(\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\p}{\partial\,}\)
- 场:
- 若在空间中,每一点上都对应着某个物理量的确定值,则在这个空间域中确定了该物理量的场
- 如果物理量为矢量,则为矢量场;若为标量,则为标量场
- 如果物理量不随时间变换,则为静态场,反之为动态场
坐标系
基本知识
- 坐标系:
- 空间中的每个点,均可用唯一一组标量表示出来,该系统就叫坐标系
- 对于 N 维空间,需要 N 个独立坐标变量
- 坐标面:
- 当一个坐标变量等于某个常数时,形成的曲面或平面
- 坐标曲线:
- 每两组坐标面的交线
- 正交坐标系:
- 过空间任意点,三条坐标曲线都互相正交的坐标系
- 坐标单位矢量:
- 过空间任意点M的三条坐标曲线的切向单位矢量
- 其模为1,以各坐标变量增加方向作为正方向
- 一个正交坐标系的坐标单位矢量相互正交并满足右手螺旋法则
下图中展示了一个以 $u_1, u_2, u_3$ 为轴的坐标系,其对应得坐标面$c_1, c_2, c_3$,坐标曲线$u_1, u_2, u_3$,坐标单位矢量 $\hat{a}_{u1}, \hat{a}_{u2}, \hat{a}_{u3}$
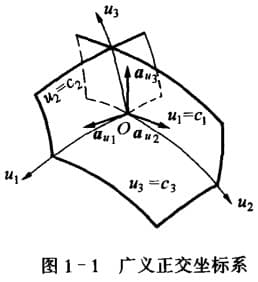
三种坐标系
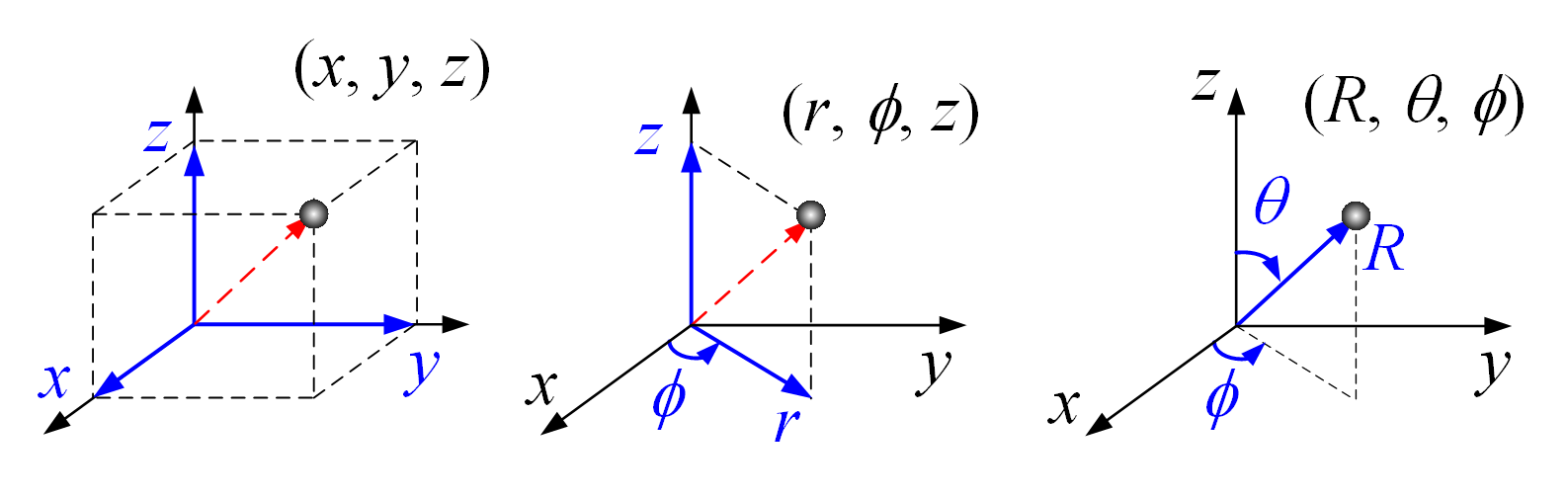
- 直角坐标系 Cartesian Coordinates
- 坐标变量:$x, y , z \; (\infty < x,y,z < \infty)$
- 任意矢量 $\vec{A}$ 表示为:$\vec{A} = A_x \hat{a}_x + A_y \hat{a}_y + A_z \hat{a}_z$
- 长度元:$\dif \vec{l} = \hat{a}_x \dif x + \hat{a}_y \dif y + \hat{a}_z \dif z$
- 面积元:
- \[\begin{align} \dif \vec{S} &= \dif S_x + \dif S_y + \dif S_z \\ &= \hat{a}_x \dif y \dif z + \hat{a}_y \dif z \dif x + \hat{a}_z \dif x \dif y \end{align}\]
- 体积元:$\dif V = \dif x\dif y\dif z$
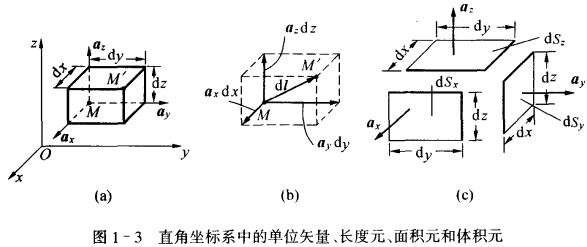
- 圆柱坐标系 Cylindrical Coordinates
- 坐标变量:$(r, \varphi, z) \; (0 \leq r < +\infty, 0 \leq \varphi \leq 2\pi, -\infty < z < +\infty)$
- 任意矢量 $\vec{A}$ 表示为:$\vec{A} = A_r \hat{a}_r + A_φ \hat{a}_φ + A_z \hat{a}_z$
- 长度元:
- \[\begin{align} \dif \vec{l} &= \dif \vec{l}_r + \dif \vec{l}_\varphi + \dif \vec{l}_z\\ &= \hat{a}_r \dif r + \hat{a}_\varphi r \dif \varphi + \hat{a}_z \dif z \end{align}\]
- 面积元:
- \[\begin{align} \dif \vec{S} &= \hat{a}_r \dif S_r + \hat{a}_\varphi \dif S_\varphi + \hat{a}_z \dif S_z\\ &= \hat{a}_r r \dif \varphi \dif z + \hat{a}_\varphi \dif r \dif z + \hat{a}_z r \dif r \dif \varphi \end{align}\]
- 体积元:$\dif V = \dif l_r \dif l_\varphi \dif z = r \dif r \dif \varphi \dif z$
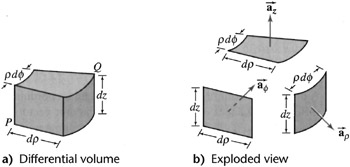
- 球坐标系 Spherical Coordinates
- $(r, \theta, \varphi) \; (0 \leq r < +\infty, 0 \leq \theta \leq \pi, 0 \leq \varphi \leq 2\pi)$
- 任意矢量 $\vec{A}$ 表示为:$\vec{A} = A_r \hat{a}_r + A_θ \hat{a}_θ + A_φ \hat{a}_φ$
- 长度元:
- \[\begin{align} \dif \vec{l} &= \dif \vec{l}_r + \dif \vec{l}_\theta + \dif \vec{l}_\varphi\\ &= \hat{a}_r \dif r + \hat{a}_\theta r \dif \theta + \hat{a}_\varphi r \sin \theta \dif \varphi \end{align}\]
- 面积元:
- \[\begin{align} \dif \vec{S} &= \hat{a}_r \dif S_r + \hat{a}_\theta \dif S_\theta + \hat{a}_\varphi \dif S_\varphi \\ &= \hat{a}_r r^2 \sin\theta \dif \theta \dif \varphi + \hat{a}_\theta r \sin\theta \dif r \dif \theta + \hat{a}_\varphi r \dif r \dif \theta \end{align}\]
- 体积元:$ \dif V = \dif l_r \dif l_\theta \dif l_\varphi = r^2 \sin \theta \dif r \dif \theta \dif \varphi$
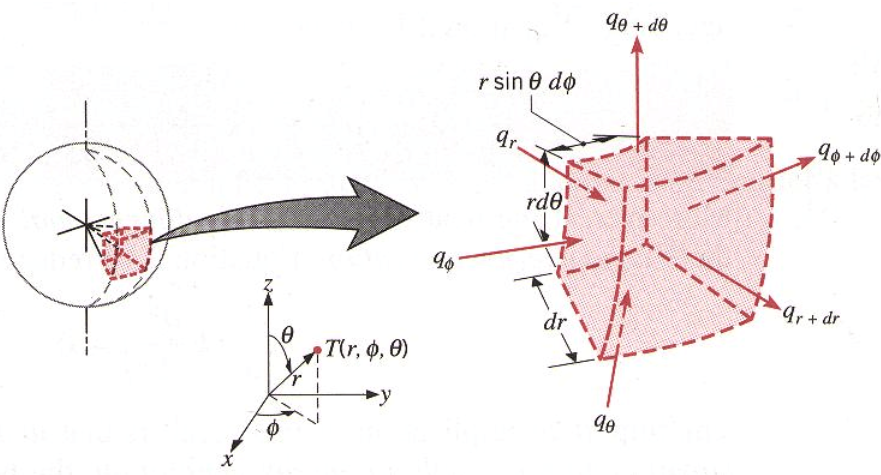

注意
- 以上三个坐标系的坐标单位矢量均是正交的
- 相比起直接记公式,记图反而更容易理解。而且很显然,后两者都是用各自坐标把 x,y,z 表示出来,比如:
坐标变量之间的关系
直角与柱
\(\begin{cases}
x = r \cos \varphi\\
y = r \sin \varphi\\
z = z
\end{cases}
\Longleftrightarrow
\begin{cases}
r = \sqrt{x^2 + y^2}\\
\varphi = \arctan \frac{y}{x}\\
z = z
\end{cases}\)
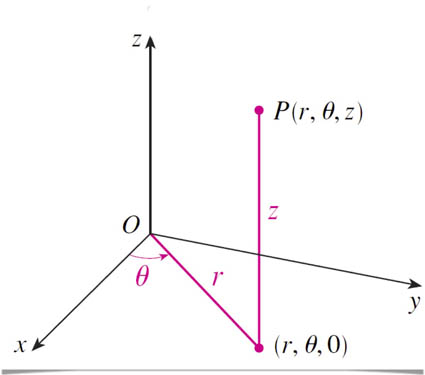
直角与球
\(\begin{cases}
x = R \sin \theta \cos \varphi\\
y = R \sin \theta \sin \varphi\\
z = R \cos \theta
\end{cases}
\Longleftrightarrow
\begin{cases}
R = \sqrt{x^2 + y^2 + z^2}\\
\theta = \arccos \frac{z}{R}\\
\varphi = \arctan \frac{y}{x}\\
\end{cases}\)
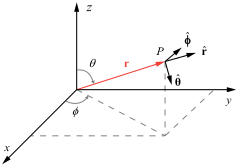
柱与球
\(\begin{cases}
r = R\sin\theta\\
\varphi = \varphi\\
z = R\cos\theta
\end{cases}
\Longleftrightarrow
\begin{cases}
R = \sqrt{r^2+z^2}\\
\theta = \arcsin \frac{r}{R} = \arccos\frac{z}{R}\\
\varphi = \varphi
\end{cases}\)
坐标单位矢量之间的关系
直角与柱
\(\begin{bmatrix}
\hat{a}_x \\ \hat{a}_y \\ \hat{a}_z
\end{bmatrix}=
\begin{bmatrix}
\cos\varphi & -\sin\varphi & 0\\
\sin\varphi & \cos\varphi & 0\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\hat{a}_r \\ \hat{a}_\varphi \\ \hat{a}_z
\end{bmatrix}\),
\(\begin{bmatrix}
\hat{a}_r \\ \hat{a}_\varphi \\ \hat{a}_z
\end{bmatrix}=
\begin{bmatrix}
\cos\varphi & \sin\varphi & 0\\
-\sin\varphi & \cos\varphi & 0\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\hat{a}_x \\ \hat{a}_y \\ \hat{a}_z
\end{bmatrix}\)
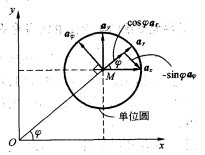
柱与球
\(\begin{bmatrix}
\hat{a}_r \\ \hat{a}_\varphi \\ \hat{a}_z
\end{bmatrix}=
\begin{bmatrix}
\sin\theta & \cos\theta & 0\\
0 & 0 & 1\\
\cos\theta & -\sin\theta & 0
\end{bmatrix}
\begin{bmatrix}
\hat{a}_R \\ \hat{a}_\theta \\ \hat{a}_\varphi
\end{bmatrix}\),
\(\begin{bmatrix}
\hat{a}_R \\ \hat{a}_\theta \\ \hat{a}_\varphi
\end{bmatrix}=
\begin{bmatrix}
\sin\theta & 0 & \cos\theta\\
\cos\theta & 0 & -\sin\theta\\
0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
\hat{a}_r \\ \hat{a}_\varphi \\ \hat{a}_z
\end{bmatrix}\)
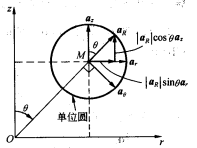
直角与球 并没有一个很直观的推导方法,最好是用柱来中转。
注意
- 单位矢量转换与坐标变量转换的思路是完全不同的。
- 坐标变量转换:利用已知的坐标通过几何运算得到未知坐标
- 单位矢量转换:将未知矢量投影到已知矢量得到系数
- 记的时候只需要记图的两个轴:$x$ 和 $y$、$r$ 和 $z$
矢量
矢量在高中、线代中已经学过,这里就直接列一些重要的。
- 矢量
- 矢量是由大小和方向的量。表示为 $\vec{A} = \vec{a}_AA$,其中,$A = \vert\vec{A}\vert$,称为 $\vec{A}$ 的模或长度;$\vec{a}_A$ 是沿 $\vec{A}$ 方向的单位矢量。
- 位置矢量
- 从原点指向空间一点 $P$ 的矢量称为 $P$ 的位置矢量,常用球坐标中的 $\vec{r}$ 表示
- 矢量运算
- (1)矢量加减运用三角法则
- (2)矢量点积 $\vec{A}\cdot\vec{B}$,满足交换律和分配律
- (3)矢量叉积 $\vec{A}\times\vec{B}$,满足分配律但不满足交换律(需要加负号),可用行列式计算。
- (4)标量三重积 $\vec{A}\cdot(\vec{B}\times\vec{C})$$=\vec{C}\cdot(\vec{A}\times\vec{B})$$=\vec{B}\cdot(\vec{C}\times\vec{A})$
- (5)矢量三重积 $\vec{A}\times(\vec{B}\times\vec{C})$$=\vec{B}(\vec{A}\cdot\vec{C})-\vec{C}(\vec{A}\cdot\vec{B})$,助记:英文谐音 BACK-CAB。相关证明
补充:后面我们会经常用到一个恒等式:$\nabla\times(\nabla\times \vec{F})=\nabla(\nabla\cdot \vec{F})-\nabla^2\vec{F}$,这个公式就是由矢量三重积得到的,至于 $\nabla$ 是啥,下一节会介绍,现在把它当一个矢量即可。
- 矢量导数
- \[\frac{\dif \vec{v}}{\dif t} = \lim_{\Delta t\rightarrow 0} \frac{\vec{v}(t+\Delta t) -\vec{v}(t)}{\Delta t}\]
- 矢量偏导
- \[\frac{\p \vec{v}}{\p x_i} = \lim_{\Delta t\rightarrow 0} \frac{\vec{v}(x_1 \cdots x_i+\Delta x_i \cdots x_n) -\vec{v}(x_1 \cdots x_i \cdots x_n)}{\Delta x_i}\]
- 矢量的求导法则
- (1)$\frac{\dif}{\dif t}[k\vec{v}] = \vec{v}\frac{\dif f}{\dif t} + f \frac{\dif \vec{v}}{\dif t}$
- (2)$\frac{\dif}{\dif t}[\vec{u}\cdot\vec{v}] = \vec{v}\cdot\frac{\dif \vec{u}}{\dif t} + \vec{u}\cdot\frac{\dif \vec{v}}{\dif t}$
- (3)$\frac{\dif}{\dif t}[\vec{u}\times\vec{v}] = \vec{v}\times\frac{\dif \vec{u}}{\dif t} + \vec{u}\times\frac{\dif \vec{v}}{\dif t}$
注意 区分:
- 常矢量:大小方向都不变的矢量
- 单位矢量:大小为1,方向可变的矢量
- 位置矢量:以坐标原点为起点的矢量
其他
对球坐标的讨论
球坐标的坐标单位矢量为 $\hat{r}, \hat{\theta}, \hat{\varphi}$(同 $\hat{a}_r, \hat{a}_\theta, \hat{a}_\varphi$),其方向是对应坐标增加的方向。与直角坐标系不同,球坐标的坐标单位矢量并不是常矢量。

我们考虑在直角坐标中的点 $(1,0,0)$ 和 $(0,1,0)$,对应球坐标的 $(1, \pi/2, 0)$ 和 $(1, \pi/2, \pi/2)$,对应的坐标单位矢量为:
- $\hat{r} = \hat{x}$,$\hat{\theta} = -\hat{z}$,$\hat{\varphi} = \hat{y}$
- $\hat{r} = \hat{y}$,$\hat{\theta} = -\hat{z}$,$\hat{\varphi} = -\hat{x}$
我们可以把 $\hat{r}, \hat{\theta}, \hat{\varphi}$ 看作是关于 $r, \theta, \varphi$ 的函数,那么函数的形式是什么呢?
我们由球-柱、柱-直之间的坐标单位矢量的关系,可以推导出球-直的坐标单位矢量的关系:
\[\begin{bmatrix} a_r \\ a_\theta \\ a_\varphi \end{bmatrix}= \begin{bmatrix} \sin\theta & 0 & \cos\theta\\ \cos\theta & 0 & -\sin\theta\\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} \cos\varphi & \sin\varphi & 0\\ -\sin\varphi & \cos\varphi & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}\]最终化简为:
\[\begin{bmatrix} a_r \\ a_\theta \\ a_\varphi \end{bmatrix}= \begin{bmatrix} \sin\theta\cos\varphi & \sin\theta\sin\varphi & \cos\theta\\ \cos\theta\cos\varphi & \cos\theta\sin\varphi & -\sin\theta\\ -\sin\varphi & \cos\varphi & 0 \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}\]我们发现,中间的矩阵中并没有 $r$,说明 $r$ 不改变 $\hat{r}, \hat{\theta}, \hat{\varphi}$. 我们进一步求出它们的偏导:
\[\frac{\p \hat{r}}{\p r}=\frac{\p \hat{\theta}}{\p r}=\frac{\p \hat{\varphi}}{\p r}=0\] \[\begin{align} \frac{\p \hat{r}}{\p \theta}&=(\cos\theta\cos\varphi, \cos\theta\sin\varphi, -\sin\theta)=\hat{\theta}\\ \frac{\p \hat{\theta}}{\p \theta}&=(-\sin\theta\cos\varphi, -\sin\theta\sin\varphi, -\cos\theta)=-\hat{r}\\ \frac{\p \hat{\varphi}}{\p \theta}&=0 \end{align}\] \[\begin{align} \frac{\p \hat{r}}{\p \varphi}&=(-\sin\theta\sin\varphi, \sin\theta\cos\varphi, 0)=\hat{\varphi}\sin\theta\\ \frac{\p \hat{\theta}}{\p \varphi}&=(-\cos\theta\sin\varphi, \cos\theta\cos\varphi, 0)=\hat{\varphi}\cos\theta\\ \frac{\p \hat{\varphi}}{\p \varphi}&=(-\cos\varphi, -\sin\varphi, 0)=-\hat{r}\sin\theta+\hat{\theta}\cos\theta \end{align}\]请记住 $\hat{r}, \hat{\theta}, \hat{\varphi}$ 的偏导,因为我们后面几章还要用。
同理,我们也可以推出柱坐标系的偏导:
\[\frac{\p \hat{a}_r}{\p r} = \frac{\p \hat{a}_\varphi}{\p r} = 0\\ \frac{\p \hat{a}_r}{\p z} = \frac{\p \hat{a}_\varphi}{\p z} = 0\\ \frac{\p \hat{a}_r}{\p \varphi} = \hat{a}_\varphi, \; \frac{\p \hat{a}_\varphi}{\p \varphi} = -\hat{a}_r\]小吐槽:说好的矢量一般用小写字母呢?咋华南理工的书这么喜欢用 $\vec{A}$ 😂 大家凑合看吧