\[\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}}\\ \newcommand{\p}{\partial}\\ \newcommand{\bd}{\boldsymbol} \end{align*}\]

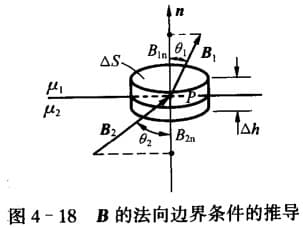
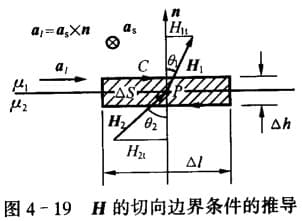
前面已经讨论过，恒定磁场的基本方程为：

\[积分形式：\begin{cases} \oint_S \bd{B} \cdot \bd{S} =0\\ \oint_C \bd{H} \cdot \dif \bd{l} = I \end{cases}\\ 微分形式 ：\begin{cases} \nabla \cdot \bd{B} =0\\ \nabla\times \bd{H}= \bd{J} \end{cases}\]

磁矢位满足：

\[\bd{B}=\nabla\times \bd{A}\\ \nabla\cdot \bd{A}=0\\ \nabla^2 \bd{A}=-\mu \bd{J}\]

对于磁介质，其表面存在磁化电流：$J_{sm}=\bd{M}\times\bd{n}$。如果是两个介质的分界面，表面磁化电流为：$J_{sm}=(\bd{M}_2-\bd{M}_1)\times\bd{n}$。由于 $J_{ms}$ 存在，使得 $B,H$ 发生突变，导致场量不连续。下面就来说明介质分界面上矢量场所满足的关系。

边界条件

法向

\[\oint_S \bd{B} \cdot \bd{S} =B_1 \cdot \bd{n} \Delta S-B_2 \cdot \bd{n} \Delta S=0\\ \therefore \bd{n}\cdot (B_1-B_2)=0 \;或\; B_{1n}=B_{2n}\]

切向

\[\oint_C \bd{H} \cdot \dif \bd{l} = \bd{H}_1\cdot \Delta \bd{l} - \bd{H}_2 \cdot \Delta \bd{l} =I\\\]

1. 若有传导电流，则：

\[\because I=\bd{J}_s \cdot \bd{a}_s\Delta l \quad \Delta\bd{l}=\bd{a}_s\times\bd{n}\Delta l\\ \therefore (\bd{H_1}-\bd{H}_2)\times (\bd{a}_s\times\bd{n}\Delta l)=\bd{J}_s \cdot \bd{a}_s\Delta l\\ \bd{n}\times(\bd{H_1}-\bd{H}_2)=\bd{J}_s \;或\; \bd{H}_{1t}-\bd{H}_{2t}=\bd{J}_s\]

1. 若没有传导电流，则：

\[\bd{n}\times(\bd{H_1}-\bd{H}_2)=0 \;或\; \bd{H}_{1t}=\bd{H}_{2t}\]

联系上面的 $B_{1n}=B_{2n}$，我们可以得到：在 $J_s=0$ 时：

\[\frac{\tan \theta_1}{\tan\theta_2}=\frac{B_{1t}/B_{1n}}{B_{2t}/B_{2n}}=\frac{B_{1t}}{B_{2t}}=\frac{\mu_1H_{1t}}{\mu_2H_{2t}}=\frac{\mu_1}{\mu_2}\]

从上式我们可以推导出以下几条结论：

• 对于 $\mu_2=\infty$ 的理想导磁体，由于 $B_2=\mu_2 H_2$ 是有限值，所以 $H_2=0$，进而 $H_{1t}=H_{2t}=0$。此时外面的磁场与理想导磁体表面垂直
• 对于铁磁-空气界面，$\mu_2 \gg \mu_1$，故 $\theta_2 \rightarrow \pi/2$，$\theta_1\rightarrow0$（磁屏蔽壳）

磁矢位的边界条件

\[\begin{cases} \nabla\cdot\bd{A}=0 \rightarrow \oint_S \bd{A}\cdot\dif \bd{S}=0\rightarrow A_{1n}=A_{2n}\\ \nabla\times\bd{A}=\bd{B} \rightarrow (\nabla\times A_1)_n=(\nabla\times\bd{A})_n\rightarrow A_{1t}=A_{2t} \end{cases}\\ \therefore \bd{A}_1=\bd{A}_2\]

边界条件总结

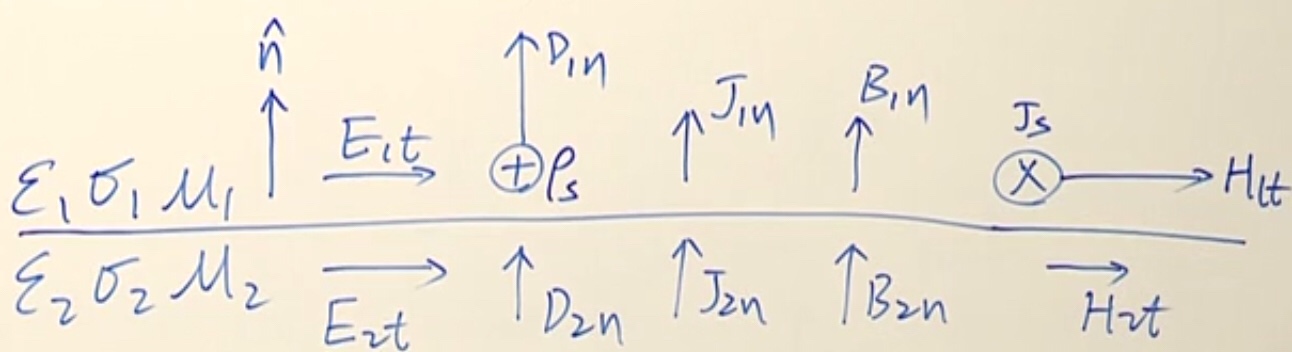
注：箭头的长短表示大小。长减短等于 0 或 $\rho_s$ 或 $J_s$