\[\begin{align*}
\newcommand{\dif}{\mathop{}\!\mathrm{d}}
\newcommand{\p}{\partial}
\end{align*}\]
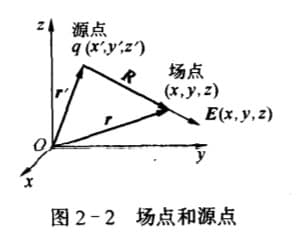
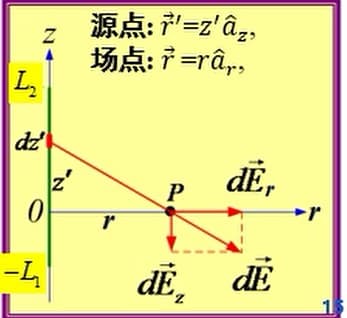
注意到直导线是柱对称的,所以我们采用柱坐标系。我们考虑 $\dif l'=\dif z'$ 上的元电荷: $$ \begin{align} \vec{R}&=r\hat{a}_r-z'\hat{a}_z\\ \dif \vec{E}&=\frac{\rho_l (r\hat{a}_r -z'\hat{a}_z) \dif z'}{4\pi\varepsilon_0 (r^2+z'^2)^{3/2}} \end{align} $$ 我们分别对 $\dif \vec{E}_r$ 和 $\dif \vec{E}_z$ 积分: $$ \begin{align} E_r&=\frac{\rho_l}{4\pi\varepsilon_0}\int_{-L_1}^{L_2} \frac{r\dif z'}{(r^2+z'^2)^{3/2}}\\ &=\frac{\rho_l}{4\pi\varepsilon_0} \end{align} $$
库伦定律
库伦定律
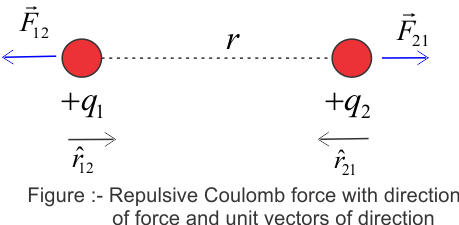
1785年法国科学家库仑由实验得出,真空中两个静止的点电荷之间的相互作用力同它们的电荷量的乘积成正比,与它们的距离的二次方成反比,作用力的方向在它们的连线上,同名电荷相斥,异名电荷相吸。即:
\[\vec{F}_{21}=\frac{q_1q_2}{4\pi \varepsilon_0 R^2}\vec{a}_R\\ 真空介电常数:\varepsilon_0\approx8.85\times10^{-12} \mathrm{C^2/(Nm^2)}\]注意下标和方向,$F_{21}$ 表示受力物体是 2,施力物体是 1,同时 $\vec{a}_R=-\vec{a}_{21}$。至于“只适用于点电荷”这个已经强调过很多次了。
 |
 |
电场强度
静电力通过电场来传递,而要描述电场,就需要电场强度。我们之前定义电场为“试验电荷所受到的力”,为了使试验电荷不影响原电场,我们进一步要求:
\[\vec{E}=\lim_{q_0\rightarrow0}\frac{\vec{F}}{q_0} \quad\text{单位:V/m 或 N/C}\]下面讨论具体电荷的电场。
点电荷
对于单个点电荷:
\[\begin{align} \vec{E}(\vec{r})&=\lim_{q_0\rightarrow0}\frac{\vec{F}}{q_0}\\ &=\frac{q\vec{a}_R}{4\pi\varepsilon_0R^2}\\ &=\frac{q}{4\pi\varepsilon_0}\frac{\vec{R}}{R^3}\\ &=-\frac{q}{4\pi\varepsilon_0}\nabla\left(\frac{1}{R}\right) (参考上一章梯度的例题) \end{align}\]我们也可以用将 $\vec{R}$ 展开为 $\vec{R}=\vec{r}-\vec{r}’$ 来表示:
\(\vec{E}(\vec{r})=-\frac{q(\vec{r}-\vec{r}')}{4\pi \varepsilon_0 |\vec{r}-\vec{r}'|^3}\)

对于多个点电荷:
\[\vec{E}(\vec{r})=\sum_{i} \vec{E}_i(\vec{r})\\ =-\frac{1}{4\pi \varepsilon_0} \sum_i\frac{q_i(\vec{r}-\vec{r}'_i)}{ |\vec{r}-\vec{r}_i'|^3}\]分布电荷
我们定义体、面、线分布电荷的密度为 $\rho$,其元电荷为:
\[体 \dif\rho=\rho \dif V'\\ 面 \dif\rho=\rho_s \dif S'\\ 线 \dif\rho=\rho_l \dif l'\]则我们可以将元电荷的看作点电荷,则:
\[体 \vec{E}(\vec{r})=-\frac{1}{4\pi\varepsilon_0} \int \rho(r')\nabla(\frac{1}{R}) \dif V'\\ 面 \vec{E}(\vec{r})=-\frac{1}{4\pi\varepsilon_0} \int \rho_s(r')\nabla(\frac{1}{R}) \dif S'\\ 线 \vec{E}(\vec{r})=-\frac{1}{4\pi\varepsilon_0} \int \rho_l(r')\nabla(\frac{1}{R}) \dif l'\]因此求分布电荷的电场强度的步骤如下:
- 选取合理微分元
- 获取微分元的电场强度表达式
- 积分
下面将求解一些均匀带电物体的电场。
均匀带电直导线的电场

注意到直导线是柱对称的,所以我们采用柱坐标系。我们考虑 $\dif l'=\dif z'$ 上的元电荷: $$ \begin{align} \vec{R}&=r\hat{a}_r-z'\hat{a}_z\\ \dif \vec{E}&=\frac{\rho_l (r\hat{a}_r -z'\hat{a}_z) \dif z'}{4\pi\varepsilon_0 (r^2+z'^2)^{3/2}} \end{align} $$ 我们分别对 $\dif \vec{E}_r$ 和 $\dif \vec{E}_z$ 积分: $$ \begin{align} E_r&=\frac{\rho_l}{4\pi\varepsilon_0}\int_{-L_1}^{L_2} \frac{r\dif z'}{(r^2+z'^2)^{3/2}}\\ &=\frac{\rho_l}{4\pi\varepsilon_0} \end{align} $$