泊松方程
高斯定理给出了电场(电位移矢量)与电荷的关系,而泊松方程则给出了电位与电荷的关系:
\[\begin{cases} \nabla \cdot \vec{D} =\rho\\ \vec{D}=\varepsilon\vec{E}\\ \vec{E}=-\nabla \phi \end{cases} \Longrightarrow \nabla^2 \phi=-\frac{\rho}{\varepsilon}\]上式即 泊松方程。特殊地,当电荷密度为 0 时,$\nabla^2 \phi=0$ 称为 拉普拉斯方程,$\nabla^2 = \frac{\p}{\p x^2}+\frac{\p}{\p y^2}+\frac{\p}{\p z^2}$ 称为拉普拉斯算子。对于不同坐标系,拉普拉斯算子分别为:
直角坐标
柱坐标
球坐标
利用 Lame 系数,可以写成:
\[\nabla^2 = \frac{1}{h_1h_2h_3} \sum_{i=1}^3 \frac{\p}{\p u_i} \left( \frac{h_1h_2h_3}{h_i} \frac{\p}{h_i \p u_i} \right)\]有时候 $\nabla^2$ 也会用于矢量,表示对分量分别求梯度的散度:
\[\nabla^2 \vec{E} = (\nabla^2 E_1) \hat{a}_1+(\nabla^2 E_2) \hat{a}_2+(\nabla^2 E_3) \hat{a}_3\]拉普拉斯算子具有与梯度与散度类似的性质:
- 分配律:$\nabla^2(u+v)=\nabla^2 u + \nabla^2 v$
- $\nabla^2(uv)=u\nabla^2 v+2\nabla u \cdot \nabla v +v\nabla^2 u$
- $\nabla \times (\nabla\times \vec{F}) = \nabla(\nabla\cdot\vec{F}) - \nabla^2\vec{F}$
边界条件
需要对 $\nabla^2 \phi$ 进行两次积分才能求得 $\phi$,这样会产生两个常数 $C_1, C_2$,因此需要两个边界条件。我们通过下面例题来体会:
已知导体球的电位为 $U$(设无穷远处的电位为0),球的半径为 $a$,求球外的电位函数。
答案
解: 以球心为坐标原点建立球坐标系。在 $a\lt r\lt \infty$ 处,电位函数满足拉普拉斯方程,并且在球外电荷密度为 0,所以:
$$
\nabla^2\phi = \frac{1}{r^2}\frac{\p}{\p r}\left(r \frac{\p \phi}{\p r} \right)=0\\
\phi=-\frac{C_1}{r}+C_2
$$
由边界条件:
$$
\begin{cases}
\phi(a)=U\\
\phi(\infty)=0
\end{cases}
\Rightarrow
\begin{cases}
C_2=0\\
C_1=-aU
\end{cases}
$$
最终解出:
$$
\phi(r)=\frac{aU}{r} \; (a<r<\infty)
$$
分界面上的边界条件
进行 $\nabla^2 \phi$ 或 $\nabla\cdot \vec{D}$ 运算的前提是“可微”,若在介质分界面上,则无法进行微分,此时只能用积分形式,而此时的边界条件只能用积分来推导。下面就介绍推导过程。
电位移的边界条件
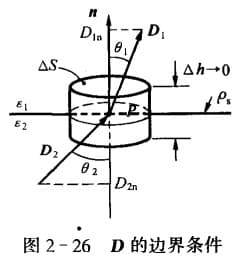
如图所示,$\vec{D}_1$ 和 $\vec{D}_2$ 对应于介质 $\varepsilon_1$ 和 $\varepsilon_2$ 的电位移矢量。我们取一无穷小的圆柱体,根据对称性,侧面上的通量为0,由高斯通量定理:
\[\oint_S \vec{D}\cdot\dif \vec{S}=\vec{D}_1\cdot\vec{n}\Delta S - \vec{D}_2\cdot\vec{n}\Delta S=\rho_s\Delta S\\ 即:\vec{n}\cdot(D_1 - D_2)=\rho_s\\ 或:D_{1n}-D_{2n}=\rho_s\]说明垂直于分界面上的电位移通量分量之差,等于界面上的自由电荷面密度。若分界面上无自由电荷,则:
\[\vec{n}\cdot\vec{D}_1=\vec{n}\cdot\vec{D}_2\\ D_{1n}=D_{2n}\]此时电位移通量在分界面上连续。
进一步,由电位移矢量与电场、电位的关系:
\[D_n=\varepsilon E_n=\varepsilon \vec{E}\cdot\vec{n}=\varepsilon(-\nabla\phi)\cdot\vec{n}=-\varepsilon\frac{\p \phi}{\p \vec{n}}\]从而有:
\[\varepsilon_1 E_{n1}-\varepsilon_2 E_{n2}=\rho_s\\ -\varepsilon_1\frac{\p \phi_1}{\p \vec{n}}+\varepsilon_2\frac{\p \phi_2}{\p \vec{n}}=\rho_2\]电场强度的边界条件
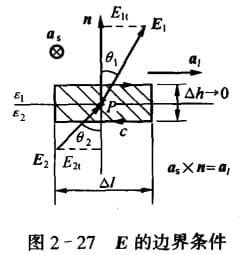
我们取一极小的闭合矩形路径,对 $E_1$ 和 $E_2$ 做线积分,由于左右的对称形,故积分为 0,从而由闭合路径电场积分为 0:
\[\oint_c \vec{E} \cdot \dif \vec{l}=\vec{E}_1 \cdot \vec{a}_l \Delta l - \vec{E}_2\cdot \vec{a}_l \Delta l =0\]我们 $\vec{a}_s$ 是垂直纸面向里的向量,即:$\vec{a}_l=\vec{a}_s\times \vec{n}$,同时由矢量恒等式:
\[\bd{A}\cdot(\bd{B}\times\bd{C})=\bd{B}\cdot(\bd{C}\times\bd{A})\\ \vec{E}\cdot(\vec{a}_s\times \vec{n})=\vec{a}_s\cdot(\vec{n}\times \vec{E})\]从而:
\[\vec{n}\times \vec{E}_1-\vec{n}\times \vec{E}_2=0\\ E_{1t}=E_1\cos\theta_1=E_2\cos\theta_2=E_{2t}\]上式说明,电场强度对于界面的切向分量在界面上是连续的,从而分界面上的电位 $\phi=\int E$ 也是连续的。注意的是,这里的连续是切线方向上的连续,上面说的是法线方向上不连续。
理想介质分界面
在两种理想介质分界面上没有自由电荷,即 $\rho_s=0$,则有:
\[\begin{cases} \vec{n}\times \vec{E}_1=\vec{n}\times \vec{E}_2\\ \varepsilon_1 \vec{E}_1\cdot\vec{n}=\varepsilon_2 \vec{E}_2\cdot\vec{n} \end{cases}\\ 即 \begin{cases} E_1\sin\theta_1=E_2\sin\theta_2\\ \varepsilon_1 E_1\cos\theta_1=\varepsilon_2E_2\cos\theta_2 \end{cases}\]将上两式相除得到:
\[\frac{\tan\theta_1}{\tan\theta_2}=\frac{\varepsilon_2}{\varepsilon_1}\]上式称为静电场的折射定理,即 $\vec{D}$ 和 $\vec{E}$ 矢量在两种介质分界面上要改变方向,除非 $\theta_1=\theta_2=0$(比如平行板、同轴线、同心球中的电场)。