\(\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*}\)
引言
从上一章的学习中,我们知道时域分析方法的基础:
- 信号在时域的分解
- LTI系统:满足线性、时不变性
而信号分解的基本信号单元必须满足:
- 本身简单,能简便求到 LTI系统的响应
- 具有普遍性,能构成广泛的信号
那么在本节中,我们将从频域来对信号与系统进行分析。而频域分解的基本信号单元也要满足上面两个特点,而显然,“频率”的最简单的函数就是“三角函数”
我们已经在高数中学过一部分傅里叶变换,但值得注意的是,高数中的傅里叶展开只适用于周期函数,如果要能构成广泛的信号,我们还需要进一步补充。
傅里叶变换的历史
在傅里叶变换之前,就已经有“泰勒展式”,也就是将函数表示成幂函数。然而,这要求函数必须任意阶可微,而且即使任意阶可微也不一定就行。所以人们就将目光投向三角函数。
然而“将函数表示成三角函数”是很反直觉的,拉格朗日就提出:
- 连续的三角函数怎么可能表示有间断点的函数?
- 奇函数$\sin x$ 怎么可能表示偶函数?
因此,欧拉、达朗贝尔、拉格朗日认为只有少部分函数能表示成三角函数。
但傅里叶并不这么认为。傅里叶是一个出身低贱,但数学天赋极佳的人。他提出每个函数都能表示为:
\[\phi(x)=\sum_{i=1}^\infty b_i\sin ix,\;0<x<\pi\]傅里叶的不同之处在于,他认为:不管在区间 $0<x<\pi$ 外怎样,这个级数在 $0<x<\pi$ 上总是等于 $f(x)$。这就是早期数学家所忽视的点。
经过傅里叶以及后来的数学家的完善,最终形成了美妙的傅里叶分析。
LTI系统对复指数信号的响应
由第一章信号,我们有一复指数信号:$e^{st}$,$s=r+j\omega$ .
根据前面的卷积积分,我们知道系统对 $e^{st}$ 的响应可以表示为:
\[y(t)=\int_{-\infty}^{\infty} e^{s(t-\tau)}h(\tau)\dif \tau=e^{st}\int_{-\infty}^\infty h(\tau) e^{-s\tau}\dif \tau=H(s)e^{st}\]- 特征函数:
- 如果系统对某一输入信号的响应只是该输入信号乘以一个常数,则称该输入信号是这个系统的特征函数,该常数称为与该信号有关(相对应)的特征值
显然,$e^{st}$ 是 LTI的特征函数,特征值 $H(s)=\int_{-\infty}^\infty h(\tau) e^{-s\tau}\dif \tau$. 同时,根据 LTI 系统的性质,对于多个复指数信号的组合 $x(t)=a_1e^{s_1t}+a_2e^{s_2t}+a_3e^{s_3t}$,对应的响应为:
\[y(t)=a_1H(s_1)e^{s_1t}+a_2H(s_2)e^{s_2t}+a_3H(s_3)e^{s_3t}\]因此,对于任意信号 $x(t)$,如果能表示成 $x(t)=\sum a_ie^{s_it}$ 的形式,并且已知特征值的表达式 $H(s)$,那么就可以求出相应的响应为 $y(t)=\sum a_iH(s_i)e^{s_it}$
同理,对于离散 LTI 系统,我们也有相同的结论:$x[n]=z^n$ 对应的响应为:
\[\begin{align} y[n]&=\sum_{k=-\infty}^{+\infty} h[k]x[n-k]\\ &=\sum_{k=-\infty}^{+\infty} h[k]z^{n-k}\\ &=z^n\sum_{k=-\infty}^{+\infty} h[k]z^{-k}\\ &\rightarrow H(z)z^n \end{align}\]对于多个复指数的线性组合 $x[n]=\sum_k a_ke^{s_kt}$,对应的输出为 $y(t)=\sum_k a_kH(s_k)e^{s_kt}$
由于复指数信号很容易求,所以我们就希望能将一般信号分解为复指数信号。
连续时间周期信号的傅里叶级数表示
我们已经在数学分析中证明过,任意一个周期为 $T_0$ 函数(包括复函数) $f(x)$ 可以展开为傅里叶级数:
\[f(x)=\frac{a_0}{2} +\sum_{n=1}^\infty (a_n\cos n\frac{2\pi}{T_0}x + b_n\sin n\frac{2\pi}{T_0}x)\\ 其中\\ a_k=\frac{2}{T_0}\int_{-T_0/2}^{T_0/2} f(x)\cos n\frac{2\pi}{T_0}x \dif x\\ b_k=\frac{2}{T_0}\int_{-T_0/2}^{T_0/2} f(x)\sin n\frac{2\pi}{T_0}x \dif x\]或者用复指数表示为:
\[x(t)=\sum_{k=-\infty}^{+\infty} a_k e^{jk\omega_0t}\\ a_k=\frac{1}{T}\int_T x(t) e^{-jk\omega_0t}\dif t\]其中,我们将 系数 ${a_k}$ 称为 $x(t)$ 的傅里叶级数系数或频谱系数,频率为 $\omega_0$ 的分量为基波,其余 $n\omega_0$ 为谐波。如果以 $k\omega_0$ 为横坐标,${a_k}$ 为纵坐标,就能绘制出 频谱图,比如下图是方波的频谱图:

傅里叶级数的收敛
虽然给出了傅里叶级数的表示,但并不意味着能求出来。比如有的时候,$a_k\rightarrow \infty$,或者 $\sum_{k=-\infty}^{\infty} a_k e^{jk\omega_0t}\rightarrow \infty$,这时显然不能分解为傅里叶级数。
比较容易看出来的是,满足下面任一条件的信号均能表示为傅里叶级数。
- 全部连续的周期信号都有一个傅里叶级数表示
- 周期信号在一个周期中具有有限能量 $\int_T \vert x(t) \vert^2 \dif t<\infty$
我们对上面的条件进行总结和补充,得到 Dirichlet 条件,包括:
条件1 $x(t)$ 在一个周期内连续或只有有限个第一类间断点(即 可去/跳跃)。
条件2 $x(t)$ 在一个周期内逐段单调(只有有限个单调区间)。
在这里说明一下,书上说的是三个条件(绝对可积、有限单调、有限个第一类间断点),和这里说的是等价的,条件一已经包含了可积了。但书本上有个表述我认为是错误的,即“最大值和最小值数目有限”(125页),一个反例就是方波,方波的最大值显然有无穷多个,但上面我们已经给出了方波的傅里叶级数。所以应该采用条件 2 的表述才准确。
Dirichlet 是能展开为傅里叶级数的充分不必要条件。有些很特殊的函数虽然不满足狄利克雷条件,依然能展开为傅里叶级数。比如“狄利克雷函数”:
\[D(x) = \begin{cases}0 & x \in \mathbb{Q} \\ 1 & x \in \mathbb{R} \setminus \mathbb{Q}\end{cases}\]其傅里叶级数的推导过程参考 the-fourier-series-of-dirichlet-function,最后推导出 $D(x)\sim1$。虽然这个结论很荒谬,但实际上是正确的。
Gibbs 现象
在间断点附近存在一点,在 $n\rightarrow\infty$ 时,其分解误差收敛于这点上的跳变值的 8.95%. 这就是 Gibbs 吉布斯现象
8.95% 的推导过程:Gibbs Phenomenon
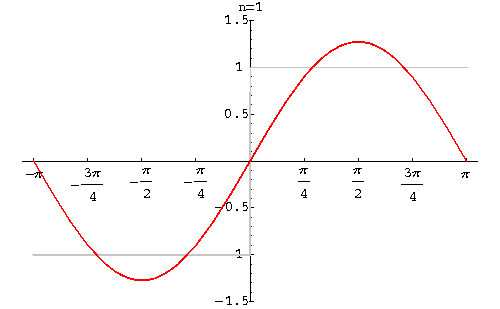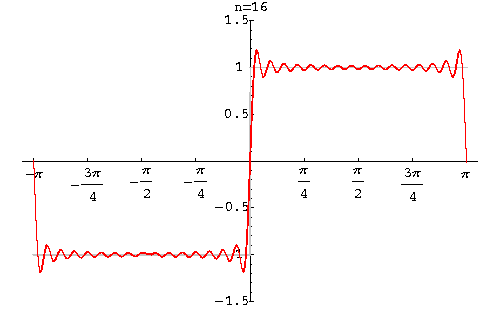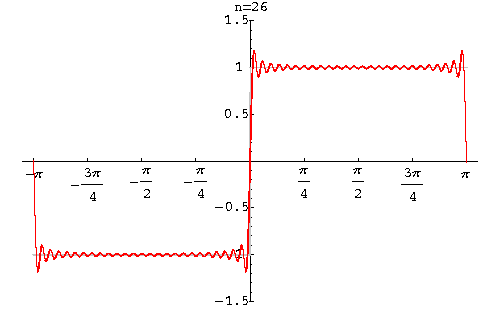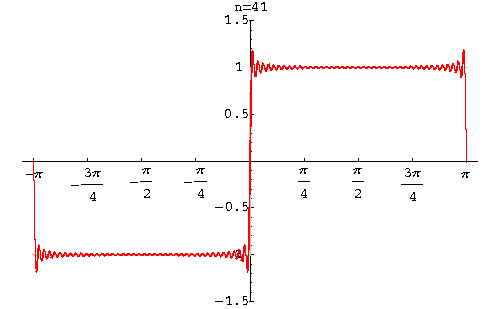
Gibbs 现象与 Dirichlet 条件不矛盾。因为他俩对“收敛”的定义并不相同,Dirichlet 指的是方均误差相等,跳变点因为宽度为0,所以这点的误差忽略不计;而 Gibbs 指的是逐点收敛,即每个点的误差都要收敛到 0。这两种收敛并不等价。
傅里叶级数的性质
用:
\[x(t) \xleftrightarrow{Fs} a_k\]表示 $x(t)$ 与傅里叶级数系数 $a_k$ 的关系。其中傅里叶级数系数:
\[a_k=\frac{1}{T}\int_T x(t) e^{-jk\omega_0t}\dif t\]线性性质
设 $x(t)$ 和 $y(t)$ 的周期同为 $T$,并且:
\[x(t)\xleftrightarrow{Fs}a_k\\ y(t)\xleftrightarrow{Fs}b_k\]则其线性组合与级数系数线性组合满足:
\[Ax(t)+By(t)\xleftrightarrow{Fs} Aa_k+Bb_k\\\]证明:
\[\begin{align} &\quad\frac{1}{T}\int_T [Ax(t)+By(t)] e^{-jk\omega_0t}\dif t\\ &=\frac{A}{T}\int_T x(t) e^{-jk\omega_0t}\dif t+\frac{B}{T}\int_T y(t) e^{-jk\omega_0t}\dif t\\ &=Aa_k+Bb_k \end{align}\]时移性质
\[x(t-t_0)\xleftrightarrow{Fs} e^{-jk\omega_0t_0}a_k\]证明:
\[\begin{align} a_k'&=\frac{1}{T}\int_T x(t-t_0) e^{-jk\omega_0 t}\dif t\\ &=\frac{1}{T}\int_T x(\tau) e^{-jk\omega_0(\tau+t_0)}\dif t\\ &=e^{-jk\omega_0t_0}\frac{1}{T}\int_T x(\tau) e^{-jk\omega_0\tau}\dif t\\ &=e^{-jk\omega_0t_0} a_k \end{align}\]注意到 $\vert e^{-jk\omega_0t_0} \vert=1$,所以 $\vert e^{-jk\omega_0t_0} a_k \vert= \vert a_k \vert$,时移不改变傅里叶级数系数的大小。
反转性质
\[x(-t)=\xleftrightarrow{Fs} a_{-k}\]证明:
\[\begin{align} x(-t)&=\sum_{k=-\infty}^{\infty} a_k e^{jk\omega_0(-t)}\\ &=\sum_{k=-\infty}^{\infty} a_k e^{j(-k)\omega_0t} \end{align}\]尺度变换
\[x(t)=\sum_{k=-\infty}^{+\infty} a_k e^{jk\omega_0t}\\ x(\alpha t)=\sum_{k=-\infty}^{+\infty} a_k e^{jk\omega_0\alpha t}\]尺度变换只会改变基波频率,不改变系数。
相乘
\[x(t)y(t)\xleftrightarrow{Fs}h_k=\sum_{l=-\infty}^{+\infty} a_l b_{k-l}\]证明:
\[\begin{align} h_k &= \frac{1}{T}\int_T x(t)y(t) e^{-jk\omega_0t}\dif t\\ &= \frac{1}{T}\int_T \left( \sum_{l=-\infty}^{+\infty} a_l e^{jl\omega_0t} \right) y(t) e^{-jk\omega_0t}\dif t\\ &= \sum_{l=-\infty}^{+\infty} a_l \left( \frac{1}{T}\int_T \left(e^{jl\omega_0t} \right) y(t) e^{-jk\omega_0t}\dif t \right)\\ &=\sum_{l=-\infty}^{+\infty} a_l \left( \frac{1}{T}\int_T y(t) e^{-j(k-l)\omega_0t}\dif t \right)\\ &=\sum_{l=-\infty}^{+\infty} a_lb_{k-l} \end{align}\]共轭与共轭对称
\[x^*(t)\xleftrightarrow{Fs} a_{-k}^*\]证明:
\[\begin{align} x^*(t)&=\sum_{k=-\infty}^{+\infty} \left( a_k e^{jk\omega_0t} \right)^*\\ &=\sum_{k=-\infty}^{+\infty} a_k^* e^{-jk\omega_0t}\\ &=\sum_{k=-\infty}^{+\infty} a_{-k}^* e^{jk\omega_0t} \end{align}\]- 若 $x(t)$ 为实函数,则 $x(t)=x^*(t)$,从而 $a_k=a_{-k}^*$.
- 若 $x(t)$ 为实偶函数,则 $a_k=a_{-k}$,从而 $a_k=a_{-k}=a_k^*$。即实偶函数的傅里叶级数系数也是实偶函数。
- 若 $x(t)$ 为实奇函数,则 $a_k=-a_{-k}$,从而 $a_k=-a_{-k}=-a_k^*$,且 $a_0=0$。即实奇函数的傅里叶级数实纯虚奇函数。
从数学上看不直观,口语化解释一下。实数函数,也就意味着 $a_k$ 和 $a_{-k}$ 的虚部要相消,所以 $a_k$ 与 $a_{-k}$ 共轭。
由于实部用欧拉公式展开就是 $\cos$,所以偶函数的傅里叶级数系数是实数;同理,奇函数的傅里叶级数是虚数。
扩展:奇谐与偶谐
有些信号只有奇数次的 $a_k$,比如方波信号,这种就叫奇谐信号;只有偶数次 $a_k$ 的就叫偶谐信号。判断方法:将一个周期分成两半,并将前半个周期平移到后半个周期,如果对称,则为奇谐,如果重合,则为偶谐。
微分
\[\frac{\dif x(t)}{\dif t}\xleftrightarrow{Fs}jk\omega_0a_k\]证明:
\[\begin{align} \frac{\dif x(t)}{\dif t}&=\frac{\dif}{\dif t} \sum_{k=-\infty}^{\infty} a_k e^{jk\omega_0t}\\ &=\sum_{k=-\infty}^{\infty} \frac{\dif}{\dif t} (a_k e^{jk\omega_0t})\\ &=\sum_{k=-\infty}^{\infty} jk\omega_0a_k \cdot e^{jk\omega_0t} \end{align}\]积分
\[\int_{-\infty}^t x(t)\dif t \xleftrightarrow{Fs} \left( \frac{1}{jk\omega_0} \right)a_k\\ 当且仅当\;a_0=0\]证明:
\[\begin{align} \int_{-\infty}^t x(t) \dif t &= \int_{-\infty}^t \left( \sum_{k=-\infty}^{\infty} a_k e^{jk\omega_0t}\right)\dif t\\ &=\sum_{k=-\infty}^{\infty} \int_{-\infty}^t (a_k e^{jk\omega_0t})\dif t\\ &=\sum_{k=-\infty}^{\infty} \left( \frac{1}{jk\omega_0} \right)a_k \cdot e^{jk\omega_0t} \end{align}\]Parseval 定理
\[\frac{1}{T}\int_T |x(t)|^2\dif t=\sum_{k=-\infty}^{+\infty} |a_k|^2\]证明:
\[设\; x(t)=a_1e^{jk_1\omega_0t}+a_2e^{jk_2\omega_0t}\\ \begin{align} 则\; \frac{1}{T}\int_T |x(t)|^2\dif t&=\frac{1}{T}\int_T \left| a_1e^{jk_1\omega_0t}+a_2e^{jk_2\omega_0t} \right|^2\dif t\\ &=\frac{1}{T}\int_T \left( a_1e^{jk_1\omega_0t}+a_2e^{jk_2\omega_0t}\right) \cdot\\ &\quad\quad\left( a_1^*e^{-jk_1\omega_0t}+a_2^*e^{-jk_2\omega_0t}\right) \dif t\\ &=\frac{1}{T}\int_T (a_1a_1^*+a_2a_2^*) \dif t\\ &=a_1^2+a_2^2 \end{align}\\ 以上证明可推广到无穷多项的情况。\quad\]汇总

其他
莫名奇妙地查到了一堆傅里叶变换的资料🤦♂️