连续时间傅里叶变换

$\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*}$

连续傅里叶变换

引入

我们考虑一个信号 $\widetilde{x}(t)$ 具有如下性质：

$\widetilde{x}(t)$ 是周期的，并且周期为 $2L$
$L$ 很大
$\widetilde{x}(t)$ 和 $x(t)$ 在 $-L<t<L$ 上具有相同值

那么，当 $L\rightarrow\infty$ 时，可以认为 $\widetilde{x}(t) = x(t)$。

我们先对 $\widetilde{x}(t)$ 进行傅里叶展开：

\[\widetilde{x}(t) = \sum_{k=-\infty}^{+\infty} a_k e^{-jk\pi t/L}\\ a_k=\frac{1}{2L} \int_{-L}^L \widetilde{x}(t) e^{-jk\pi t/L} \dif t=\frac{1}{2L} \int_{-L}^L x(t) e^{-jk\pi t/L} \dif t\]

代入 $a_k$ 的表达式到傅里叶展式中的 $a_k$：

\[\widetilde{x}(t) = \sum_{k=-\infty}^{+\infty} \left[ \frac{1}{2L} \int_{-L}^L x(u) e^{-jk\pi u/L}\dif u \right] e^{-jk\pi t/L}\]

同时对 $k$ 进行如下替换：

\[\Delta\omega=\frac{\pi}{L} \quad \omega_k=\frac{k\pi}{L}\]

$\Delta\omega$ 表示相邻 $\omega_k$ 间的距离。代入傅里叶展式：

\[\begin{align} \widetilde{x}(t) &= \sum_{k=-\infty}^{+\infty} \left[ \frac{\Delta\omega}{2\pi} \int_{-L}^L x(u) e^{-j\omega_k u}\dif u \right] e^{j\omega_k t}\\ &=\frac{1}{2\pi} \sum_{k=-\infty}^{+\infty} \left[ \int_{-L}^L x(u) e^{-j\omega_k u}\dif u \right] e^{j\omega_k t} \Delta\omega\\ &=\frac{1}{2\pi} \sum_{k=-\infty}^{+\infty} F(\omega_n) \Delta\omega \end{align}\\ 其中，F(\omega_n)=\left[ \int_{-L}^L x(u) e^{-j\omega_k u}\dif u \right] e^{-j\omega_k t}\]

当 $L\rightarrow\infty$ 时，$\Delta\omega\rightarrow 0$，$\omega_k\rightarrow\omega$（离散变连续），所以：

\[x(t)=\lim_{L\rightarrow\infty}\widetilde{x}(t)= \frac{1}{2\pi} \lim_{\Delta\omega\rightarrow 0}\sum_{k=-\infty}^{+\infty} F(\omega_n) \Delta\omega\\ 其中，F(\omega_n)=\left[ \int_{-\infty}^{+\infty} x(u) e^{-j\omega u}\dif u \right] e^{-j\omega t}\]

注意到，对于任何积分，我们都可以表示成：

\[\int_a^b f(x)\dif x=\lim_{\Delta x\rightarrow}\sum_{n=1}^{N} f(x_n)\Delta x\]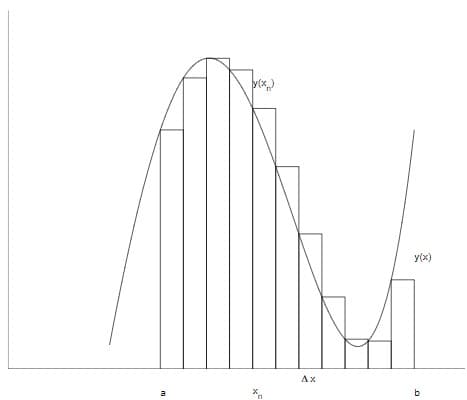

那么我们有：

\[\begin{align} x(t)&= \frac{1}{2\pi} \lim_{\Delta\omega\rightarrow 0}\sum_{k=-\infty}^{+\infty} F(\omega_n) \Delta\omega\\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} F(\omega_n) \dif \omega\\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} \left[ \int_{-\infty}^{+\infty} x(u) e^{-j\omega u}\dif u \right] e^{j\omega t} \dif \omega\\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} X(\omega) e^{j\omega t} \dif \omega \end{align}\]

我们将 $X(\omega)$ 称作 $x(t)$ 的 傅里叶变换 或 傅里叶积分 或频谱（奥本海姆教材中写作 $X(j\omega)$，考试时也这样写）。根据上面一系列的变换，我们可知 $X(\omega)$ 与 $x(t)$ 之间的变换公式为：

\[X(\omega)=\int_{-\infty}^{+\infty} x(t) e^{-j\omega t}\dif t\\ x(t)=\frac{1}{2\pi} \int_{-\infty}^{+\infty} X(\omega) e^{j\omega t} \dif \omega\]

这两条公式称 傅里叶变换对，第一条为 傅里叶变换（Fourier transform），第二条为 傅里叶逆变换（inverse Fouriertransform）。

最后我们讨论一下 $X(\omega)$ 与 $a_k$ 的关系。如果 $x(t)$ 只在一个周期内等于 $\widetilde{x}(t)$，并且在其他周期为 0，则：

\[a_k=\frac{1}{T}X(k\omega_0)=\frac{1}{T}\int_T x(t) e^{-jk\omega_0t}\dif t\]

收敛条件

傅里叶变换中 $\lim_{t\rightarrow\pm\infty}e^{-j\omega t}$ 趋向于正无穷，所以 $\lim_{t\rightarrow\pm\infty} x(t)$ 必须趋向于 0，这样才能使 $\lim_{t\rightarrow\pm\infty} x(t)e^{-j\omega t}$ 为有限值。

因此我们有如下定理：

The Fourier integral transform of the function $h(t)$,

\[H(\omega)=\int_{-\infty}^{+\infty} h(\omega)e^{-j\omega t} \dif t\]

will exist if either

\[\int_{-\infty}^{+\infty} |h(t)|^2\dif t<\infty \quad \rm{or} \quad \text{satisfy Dirichlet Conditions}\]

Dirichlet Conditions in Fourier Transformation are as follows:

f(x) must absolutely integrable over a period（绝对可积）, which is:
\[\int_{-\infty}^{+\infty} |h(t)| \dif t<\infty\]
f(x) must have a finite number of exterma in any given interval, i.e. there must be a finite number of maxima and minima in the interval（有限区间内最值有限）.
f(x) must have a finite number of discontinues in any given interval, however the discontinuity cannot be infinite.（有限区间内有有限第一间断点）

依然强调地是，以上均为充分不必要条件。后面我们会发现某些函数不满足以上条件依然可以进行傅里叶变换。

上面我们已知傅里叶变换为：

\[\begin{align} x(t) &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} X(\omega) e^{j\omega t} \dif \omega\\ &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} \left[ \int_{-\infty}^{+\infty} x(u) e^{-j\omega u}\dif u \right] e^{j\omega t} \dif \omega \end{align}\]

我们改变一下积分顺序：

\[\begin{align} x(t)&=\frac{1}{2\pi}\int_{-\infty}^{+\infty} x(u) \left[ \int_{-\infty}^{+\infty} e^{-j\omega u} e^{j\omega t} \dif \omega \right] \dif u\\ &=\frac{1}{2\pi}\int_{-\infty}^{+\infty} x(u) \left[ \int_{-\infty}^{+\infty} e^{j\omega (t-u)} \dif \omega \right] \dif u \end{align}\]

注意到：

\[\int_{-\infty}^{+\infty} e^{j\omega (t-u)} \dif \omega=\delta(t-u)\]

从而：

\[\begin{align} x(t)&=\frac{1}{2\pi}\int_{-\infty}^{+\infty} x(u) \delta(t-u) \dif u \end{align}\]

常见信号的傅里叶变换

矩形脉冲信号

\[x(t)= \begin{cases} 1 & |t|<T_1\\ 0 & |t|>T_1 \end{cases}\\ X(j\omega)=\int_{-T_1}^{T_1} e^{-j\omega t}\dif t=2\frac{\sin\omega T_1}{\omega}\]

为了有更直观的了解，我们在 MATLAB 中模拟求解连续傅里叶变换并作出图像：

t=-1:.01:1; %T1
k=0;
for f=-5:.01:5
    k=k+1;
    X(k)=trapz(t, exp(-j*2*pi*f*t)); %傅里叶变换
    end
f=-5:.01:5;
plot(f,X)

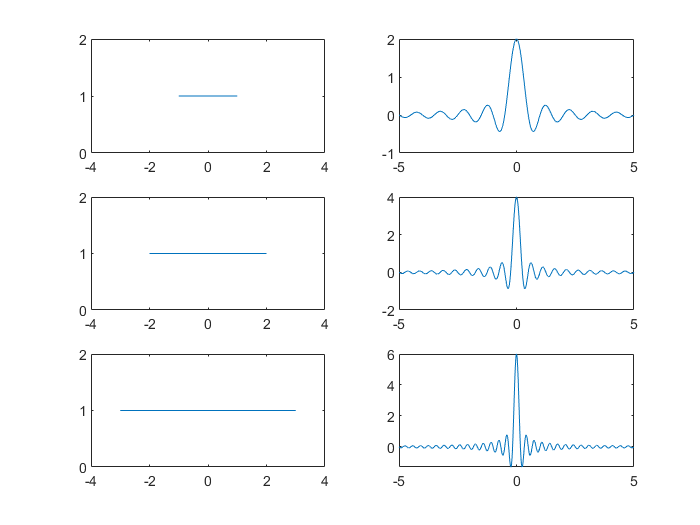
从图中可以看出，矩形脉冲信号的时间越长，带宽越窄，傅里叶变换越“趋近”冲激信号。实际上，冲激信号的一种表示方法就是：$\lim_{\omega\rightarrow\infty} \frac{\omega\sin\omega t}{\pi t}$。

定义：$\rm{sinc}(\theta)=\dfrac{\sin(\pi\theta)}{\pi\theta}$，$\rm{Sa}(\theta)=\dfrac{\sin\theta}{\theta}$。则矩形脉冲信号的傅里叶变换：

\[X(j\omega)=2T_1\rm{Sa}(\omega T_1)=2T_1\rm{sinc}(\frac{\omega T_1}{\pi})\]

补充：如果矩形信号的边缘没这么“直上直下”，那么带宽会变窄。所以如果想要减少电磁干扰，可以通过改变信号边缘的斜率，减小电磁信号的带宽。（不会考，但以后设计会用到）

冲激信号

根据冲激信号的筛选性质，我们有：

\[X(j\omega)=\int_{-\infty}^{+\infty} \delta(t) e^{-j\omega t}\dif t\\ =\int_{-\infty}^{+\infty} \delta(t) e^{-j\omega 0}\dif t=1\]

这说明冲激信号的傅里叶变换具有所有的频率分量，从这一角度也能说明为什么冲激信号可以用来表示所有信号。

联系上面的矩形脉冲信号，我们可以发现，当矩形脉冲信号的宽度趋向于无穷时，其傅里叶变换类似于冲激信号。所以我们可以认为：冲激与矩形互为傅里叶变换。

表 4-2

周期信号的傅里叶变换

假设有一信号的傅里叶变换表示为：

\[X(j\omega)=2\pi\delta(\omega-\omega_0)\]

那么傅里叶逆变换的到该信号为：

\[x(t)=\frac{1}{2\pi} \int_{-\infty}^{+\infty} 2\pi\delta(\omega-\omega_0) e^{j\omega t} \dif \omega=e^{j\omega_0 t}\]

我们注意到 $e^{j\omega_0 t}$ 是傅里叶级数的基本信号，那么假如一个周期信号可以展开为傅里叶级数，那么其傅里叶变换可以表示为：

\[X(j\omega)=\sum_{k=-\infty}^{+\infty} 2\pi a_k \delta(\omega-k\omega_0)\\ x(t)=\sum_{k=-\infty}^{+\infty} a_k e^{j\omega_0 t}\]

比如对于 $x(t)=\sin(t)$，$X(j\omega)=$

上篇离散时间傅里叶级数

下篇连续时间傅里叶变换的性质