\(\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \newcommand{\F}{\mathcal{F}} \newcommand{\ft}{\xleftrightarrow{\F}}\)
由于计算机只能处理离散时间信号,如果要处理连续时间信号,需要先进行连续到离散的转换(coutinuous-to-discrete time conversion, C/D转换),然后经过离散系统处理后,再用离散到连续时间转换(discrete-continuous time conversion, D/C转换),得到连续时间信号。
C/D转换又称为模数转换(A/D),D/C转换又称为数模转换(D/A)
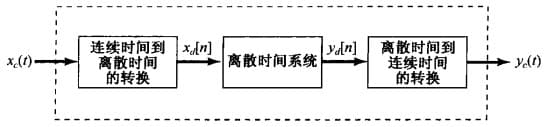
下面我们为了区分各个信号,用下列角标:
- $x_c(t)$ 表示输入的连续信号
- $x_d[n]$ 表示连续信号经过 C/D 转换得到的离散信号
- $y_d[n]$ 表示输出的离散信号
- $y_c(t)$ 表示离散信号经过 D/C 转换得到的连续信号
C/D转换
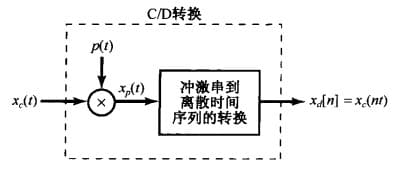
我们可以用以下公式表示采样:
\[x_p(t)=x_c(t)p(t)=\sum_{n=-\infty}^{+\infty} x_c(nT)\delta(t-nT)\]在这里强调一点,就是经过采样的信号依然不是离散信号。首先,冲激信号本身就不是离散信号,两个连续信号相乘不能的到离散信号。其次,得到的样本序列的时间轴也不一定是整数的。因此,我们构建一个离散序列 $x_d[n]$,令它满足:
\[x_d[n]=x_p(nT)=x_c(nT)\]对 $x_p(t)$ 和 $x_d[n]$ 进行傅里叶变换:
\[\begin{align} X_p(j\omega)&=\int_{-\infty}^{+\infty} x_p(t) e^{-j\omega t}\dif t\\ &=\int_{-\infty}^{+\infty} \left[ \sum_{n=-\infty}^{+\infty} x_c(nT)\delta(t-nT) e^{-j\omega t} \right]\dif t\\ &=\sum_{n=-\infty}^{+\infty} x_c(nT) \int_{-\infty}^{+\infty} \delta(t-nT) e^{-j\omega t} \dif t\\ &=\sum_{n=-\infty}^{+\infty} x_c(nT)e^{-j\omega nT} \end{align}\] \[\begin{align} X_d(e^{j\Omega}) &= \sum_{-\infty}^{+\infty} x_d[n] e^{- j\Omega n}\\ &= \sum_{-\infty}^{+\infty} x_c(nT) e^{- j\Omega n} \end{align}\]上面我们用 $\omega$ 和 $\Omega$ 来区分两个频谱。比较两个傅里叶变换,有:
\[X_d(e^{j\Omega})=X_p(j\Omega/T) \rightarrow \omega=\frac{\Omega}{T}\\ 逆过程 X_p(j\omega)=X_d(e^{j\omega T}) \rightarrow \Omega=\omega T\]或者也可以用频域卷积性质来求,同样也能得到 $\omega$ 和 $\Omega$ 的关系:
\[X_p(j\omega)=\frac{1}{T} \sum_{k=-\infty}^{+\infty} X_c(j(\omega-k\omega_s)), \omega_s=2\pi/T\\ X_d(e^{j\Omega})=\frac{1}{T} \sum_{k=-\infty}^{+\infty} X_c(j(\Omega-2\pi k)/T)\]这个有点类似于傅里叶变换的尺度变换性质:时域上的拉伸 $x_p(nT)$ 对应于频域上的压缩 $X_p(j\Omega/T)$(但少了系数)。冲激采样的频谱是以 $2\pi/T$ 为周期的,而离散傅里叶变换是以 $2\pi$ 为周期的,所以冲激串到离散序列的转换本质上就是尺度变换($\frac{2\pi}{T} \times T=2\pi$)。(如下图)
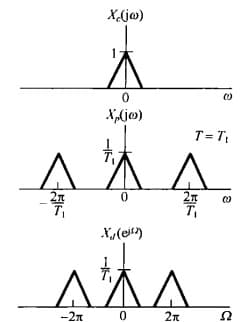
$x_p(t)$ 时间轴上原本是以 $T$ 为间隔的,经过这样的变换后,$x_d[n]$ 则是变为了以 $1$ 为间隔。我们将这种变换称为 归一化。
D/C转换
将上述步骤逆过来就是能将离散信号转化为连续信号:
\[\begin{cases} x_p(nT)=x[n]\\ X_p(j\omega)=Y_d(e^{j\omega T}) \end{cases}\\ \Downarrow\\ 低通滤波\\ \Downarrow\\ x(t)\]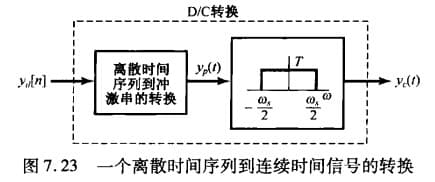
利用离散系统处理连续信号
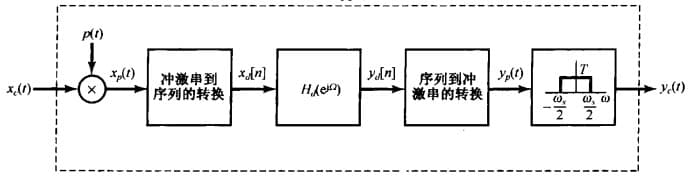
C/D转化 与 D/C转换互为逆过程,通过这个我们就能用离散系统处理连续信号,也就是说,上图虚线框中的系统相当于一个线性时不变系统。在这里提出一个问题:$x_c(t)p(t)$ 并不是一个时不变环节,为什么整个系统还能等效为一个线性时不变系统?
将离散系统 $H_d(e^{j\Omega})$ 转换为连续系统,先是进行尺度变换得到 $H_d(e^{j\omega T})$,然后再滤波得到:
\[H_c(j\omega)= \begin{cases} H_d(e^{j\omega T}) & |\omega|<\omega_s/2\\ 0 & |\omega|>\omega_s/2 \end{cases}\]下面用具体例子来讨论。
数字微分器
根据傅里叶变换的微分性质,我们知道微分器为:
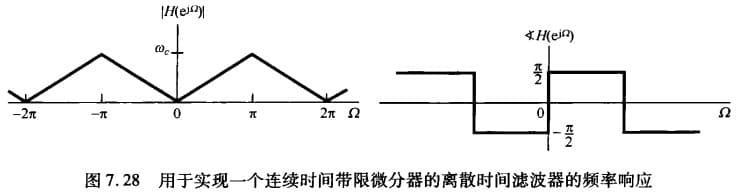
\[H_c(j\omega)=j\omega\]在这个基础上加上低通滤波就得到带限微分器(图像如下):
\[H_c(j\omega)= \begin{cases} j\omega & |\omega|<\omega_c\\ 0 & |\omega|>\omega_c \end{cases}\]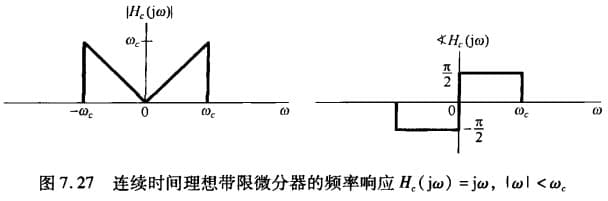
利用 C/D 转换的关系,假如采样频率为 $\omega_s=2\omega_c$,则上面的连续时间频率响应转化为离散时间频率响应为:
\[H_d(e^{j\Omega})=j\left( \frac{\Omega}{T} \right), |\Omega|<\pi\]