\(\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \newcommand{\L}{\mathcal{L}} \newcommand{\ft}{\xleftrightarrow{\F}} \newcommand{\red}[1]{\color{orangered}{#1}}\)
拉普拉斯变换的引入
拉普拉斯变换实际上是傅里叶变换的推广,其适用范围更广,并且能进一步简化系统求解。
实际上,我们在 连续时间傅里叶级数 中已经提过,线性时不变系统的特征函数是 $e^{st}$,$s=\sigma+j\omega$,其响应为:
\[y(t)=H(s)e^{st}\]在傅里叶级数与傅里叶变换中,$s=j\omega$,如果将 $s$ 扩展到整个复数域,令 $s=\sigma+j\omega$,那么就得到拉普拉斯变换:
\[X(s)=\int_{-\infty}^{+\infty} x(t)e^{-st}\dif t=\int_{-\infty}^{+\infty} x(t)e^{-\sigma t} e^{-j\omega t}\dif t\\\]上式可以看作是 $x(t)e^{-\sigma t}$ 的傅里叶变换。由于我们乘了一个“衰减因子” $e^{-\sigma t}$,这么一来,一些不满足狄利克雷条件的信号就可积。因此适用范围比傅里叶变换广。
对应的傅里叶反变换为:
\[x(t)e^{-\sigma t}=\frac{1}{2\pi} \int_{-\infty}^{+\infty} X(s) e^{j\omega t}\dif \omega\\ x(t)=\frac{1}{2\pi} \int_{-\infty}^{+\infty} X(s) e^{(\sigma+j\omega)t}\dif \omega\]我们用 $\dif s$ 代替 $\dif \omega$,由于 $\sigma$ 可以看作常数,故有拉普拉斯反变换:
\[x(t)=\frac{1}{2\pi j} \int_{-\infty+\sigma}^{+\infty+\sigma} X(s) e^{st} \dif s\]总结:拉普拉斯正变换 与 拉普拉斯反变换:
\[X(s)=\int_{-\infty}^{+\infty} x(t)e^{-st}\dif t\\ x(t)=\frac{1}{2\pi j} \int_{-\infty+\sigma}^{+\infty+\sigma} X(s) e^{st} \dif s\]$X(s)$ 又称为 象函数,$x(t)$ 又称为 原函数。
收敛域
上面说了,$e^{-\sigma t}$ 是一个衰减因子,$\sigma$ 的取值不同,衰减的速度也不同。如果衰减速度过慢,则 $x(t)e^{-\sigma t}$ 就不收敛。因此,我们定义 收敛域 为使 $X(s)$ 存在的 $s$ 的区域,简记为 ROC(region of convergence),也就是拉氏变换的存在条件。
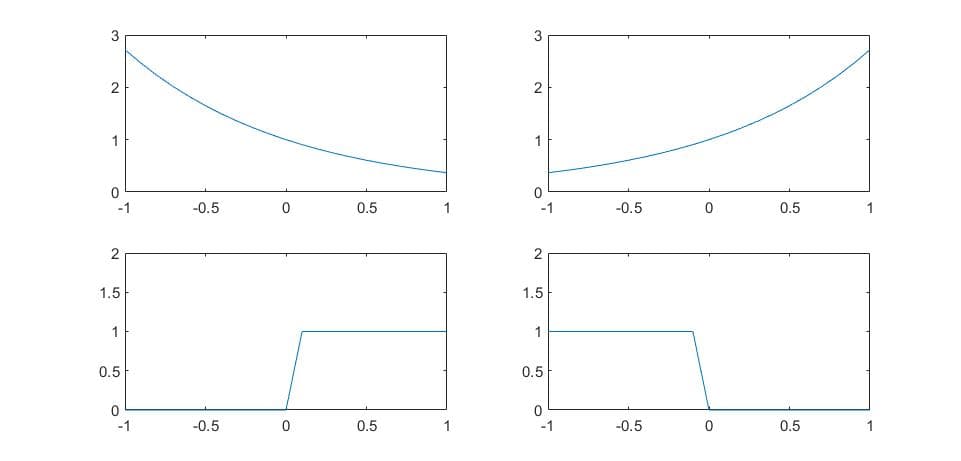
由于 $\sigma$ 的取值不同,其衰减的方向也不同:
- $\sigma>0$,$x(t)$ 是右边信号(只有 $t>0$ 时有值),则存在 $\sigma_1$,对 $\forall \sigma>\sigma_1$,$\lim_{t\rightarrow+\infty} x(t) e^{-\sigma t}=0$。 此时,ROC: $\sigma>\sigma_1$
- $\sigma<0$,$x(t)$ 是左边信号(只有 $t>0$ 时有值),则存在 $\sigma_2$,对 $\forall \sigma>\sigma_2$,$\lim_{t\rightarrow-\infty} x(t) e^{-\sigma t}=0$。 此时,ROC: $\sigma>\sigma_2$
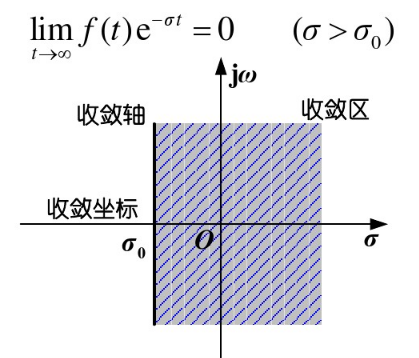
比如考虑 指数阶信号 $x(t)=e^{\sigma_0 t} u(t)$,若 $\sigma_0<0$,则要使 $\lim_{t\rightarrow+\infty} e^{(\sigma_0-\sigma) t}=0$,$\sigma>\sigma_0$,收敛域(ROC)为:$\sigma>\sigma_0$(如下图)
这里介绍几个常用的判断收敛域的法则:
- 指数阶信号的收敛域为 $\sigma > \sigma_0$(右边信号) 或 $\sigma > \sigma_0$(左边信号)
- 有界的非周期信号的拉氏变换一定存在
- 可以通过增长速度判断收敛域:
- $t^n$ 信号比 $e^{t}$ 增长慢,故 $t^n$ 的 ROC 为 $\sigma > 0$
- $e^{t^2}$ 比指数信号增长快,故 ROC 不存在
注意 求拉氏变换时必须写出 ROC
常用信号拉普拉斯变换
用 $\L[x(t)]$ 表示拉氏变换。
阶跃信号
\[\begin{align} \L [u(t)]&=\int_{0_-}^{+\infty} 1 \cdot e^{-st} \dif t\\ &= \frac{1}{-s} e^{-st} \Big\vert_{0_-}^{+\infty}\\ &= \frac{1}{s} \end{align}\\ 令 \lim_{t\rightarrow+\infty} e^{-\sigma t}=0,\text{则ROC为 } \sigma>0\]单边指数信号
\[\begin{align} \L[ e^{-s_0 t}u(t)] &=\int_{0_-}^{+\infty} e^{-s_0 t} \cdot e^{-st} \dif t\\ &= \frac{e^{-(s_0+s)t}}{-(s_0+s)} \Bigg\vert_{0_-}^{+\infty} \end{align}\\ 令 \lim_{t\rightarrow+\infty} e^{-s_0 t} e^{-\sigma t}=0,\\ 即 \lim_{t\rightarrow+\infty} e^{-(\alpha+\sigma) t}=0\\ \text{则ROC为 } \sigma>-\alpha\\\]注:$s_0=\alpha+j \omega_0$
冲激信号
\[\L[\delta(t)]=\int_{0_-}^{+\infty}\delta(t) \cdot e^{-st} \dif t=1\\ \text{ROC 为全平面}\]右边指数信号
\[\begin{align} \L [ t^nu(t)] &= \int_{0_-}^{+\infty} t^n \cdot e^{-st} \dif t\\ 分部积分&= \int_{0_-}^{+\infty} t^n \frac{1}{-s} \dif e^{-st}\\ &= \frac{e^{-st}}{-s} t^n \Big\vert^{+\infty}_{0_-}-\frac{n}{-s} \int_{0_-}^{+\infty} t^{n-1} e^{-st}\dif t\\ &= \frac{n}{s} \int_{0_-}^{+\infty} t^{n-1} e^{-st}\dif t\\ &= \frac{n}{s} \L [ t^{n-1}u(t)] \end{align}\\ 令 \lim_{t\rightarrow+\infty} t^n e^{-\sigma t}=0,\text{则ROC为 } \sigma>0\]由于 $\L[u(t)]=\dfrac{1}{s}$,则由递推关系,得到:
\[\L[t^n u(t)]=\frac{n!}{s^{n+1}}\]拉普拉斯逆变换
如果按照定义式来求复变函数积分,会很复杂。我们可以利用已知拉普拉斯变换对,或留数定理来求。
围线积分法(留数定理)
设 $s_1,s_2,\cdots,s_n$ 为 $X(s)$ 的所有奇点,且 $s\rightarrow 0$ 时,$X(s)\rightarrow 0$,则:
\[x(t)=\frac{1}{2\pi j} \int_{-\infty+\sigma}^{+\infty+\sigma} X(s) e^{st} \dif s=\sum_{k=1}^n \mathrm{Res}_{s=s_k} [X(s)e^{st}]\]关于留数,可以看复变函数的相关内容。这里简单贴一下留数的计算方法(来自Todd Zhou的笔记):

部分分式展开法
首先要知道典型信号的拉式变换表:
\[\begin{align} 无极点:&\L [\delta(t)]=1 \quad \L[\delta^{(n)}(t)]=s^n\\ 极点在虚轴:&\L[u(t)]=\frac{1}{s} \quad \L[t]=\frac{1}{s^2} \quad \L[t^n]=\frac{n!}{s^{n+1}}\\ &\L[\cos(\omega_0 t)]=\frac{s}{s^2+\omega_0^2} \quad \L[\sin(\omega_0 t)]=\frac{\omega_0}{s^2+\omega_0^2}\\ 极点在实轴:&\L[e^{-\alpha t}]=\frac{1}{s+\alpha} \quad \L[e^{-\alpha t}\cos(\omega_0 t)]=\frac{s+\alpha}{(s+\alpha)^2+\omega_0^2} \\ & \L[e^{-\alpha t}\sin(\omega_0 t)]=\frac{\omega_0}{(s+\alpha)^2+\omega_0^2} \end{align}\]而一般 $X(s)$ 具有如下的有理分式形式:
\[X(s)=\frac{B(s)}{A(s)}=\frac{b_m s^m+\cdots+b_1 s+b_0}{a_n s^s+\cdots +a_1 s+a_0}\\ a_i,b_i为实数,m,n为正整数\]作因式分解:
\[X(s)=\frac{B(s)}{A(s)}=\frac{b_m(s-z_1)(s-z_2)\cdots(s-z_m)}{a_n(s-p_1)(s-p_2)\cdots(s-p_n)}=K\frac{\prod_{i=1}^m(s-z_i)}{\prod_{i=1}^n (s-p_i)}\]其中,$z_1,\cdots,z_m$ 是 $B(s)=0$ 的根,称为 $X(s)$ 的 零点;$p_1,\cdots,p_n$ 是 $A(s)=0$ 的根,称为 $X(s)$ 的 极点
比较常见的是下面三种形式:
| $X(s)$ | 利用的变换对 |
|---|---|
| $$ \frac{1}{(s-p_1)(s-p_2)}=\frac{k_1}{s-p_1}+\frac{k_2}{s-p_2}\\ p_i 为各不相同的实数根 $$ | $$ \frac{k}{s-p} \xleftrightarrow{} e^{pt} u(t) $$ |
| $$ \frac{1}{(s-p)(s-p^*)}=\frac{1}{s^2-(p+p^*)s+pp^*} $$ | $$ \L[e^{-\alpha t}\sin(\omega_0 t)]\\ \L[e^{-\alpha t}\cos(\omega_0 t)] $$ |
| $$ \frac{1}{(s-p_1)^2(s-p_3)}=\frac{k_1}{s-p_1}+\frac{k_2}{(s-p)^2} +\frac{k_3}{s-p_3}$$ | $$ t^n u(t)\xleftrightarrow{} \frac{n!}{s^(n+1)} $$ |
至于展开式分子 $k_1,k_2\cdots$ 怎么求,这里介绍一个比较快捷的方法(亥维赛德掩盖cover-up法):
\[考虑:\frac{s+1}{(s+2)(s+3)}=\frac{k_1}{s+2}+\frac{k_2}{s+3}\\ 对左右两边同乘 s+2:\frac{s+1}{s+3}=k_1+\frac{k_2}{s+3}(s+2)\\ 然后令 s=-2:-1=k_1\\ 同理可得:2=k_2\]但掩盖法只适用于实数根和重根(注:计算重根时,$k_1$ 需要借助求导,$k_2$同上),如果是共轭根,需要老老实实地用待定系数法。
特殊情况:
- 非真分式(分子次数大于分母):利用长除法转化为多项式+真分式,多项式部分可以利用 $\delta(t)$ 以及 s域微分性质;
- 分子含有 $e^{-s\tau}$ 项,可以先将其取出来,通过时移性质再变回去。
- 含 $\frac{1}{1-e^{-sT}}$ 项(周期变换因子),则先将其取出来,然后再进行周期变换
拉普拉斯变换的性质
以下都是指单边变换,即 $x(t)u(t)$。
线性性质
\[\L[a x_1(t)+bx_2(t)]=a \L[x_1(t)]+b \L[x_2(t)]\\ 收敛域取交集,收敛域不包含任何极点\]求 $\cos (\omega_0 t) u(t)$ 的拉普拉斯变换
解:已知 $\L[e^{-s_0 t}]=\dfrac{1}{s+s_0}$
则
$$
\L[\cos(\omega_0t)]=\frac{1}{2} \left( \frac{1}{s-j\omega_0}+\frac{1}{s+j\omega_0} \right)=\frac{s}{s^2+\omega_0^2}
$$
这里引入极点与零点的概念:
- $X(s)$ 分母多项式的根 $p_1,\cdots,p_n$ 称为极点
- $X(s)$ 分子多项式的根 $z_1,\cdots,z_n$ 称为零点
在 $s$ 平面上用 ❌ 表示极点,用 ⭕ 表示零点,则上述例题的 零极点图 为:
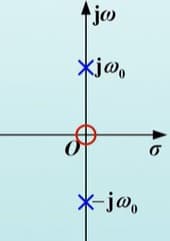
时移性质
若 $\L[x(t)]=X(s)$,则 $\L[f(t-t_0)u(t-t_0)]$($t_0>0$)的拉普拉斯变换为 $X(s)e^{-s t_0}$
证明
s域平移
\[\L[x(t)e^{-\alpha t}]=X(s+\alpha)\\ \alpha 为复数\]证明
尺度变换
\[\L [x(\red{a}t)]=\red{\frac{1}{a}} X(\frac{s}{\red{a}})\]证明略。
卷积
其中,$x_1(t),x_2(t)$ 为有始信号。
\[\L[x_1(t)*x_2(t)]=X_1(s)X_2(s)\\ \L[x_1(t)x_2(t)]=\frac{1}{2\pi j} X_1(s)*X_2(s)\]证明
单边周期信号的拉氏变换
解:设 $f_0(t)$ 是单边信号,对 $f_0(t)$ 进行单边周期重复。即:
$$
f(t)=f_0(t)*\delta_T(t)\\
\delta_T(t)=\delta(t)+\delta(t-T)+\cdots
$$
则对应的拉氏变换为:
$$
\begin{align}
\L[\delta_T(t)]&=1+e^{-sT}+e^{-s2T}+\cdots\\
&=\frac{1}{1-e^{-sT}}
\end{align}\\
\L[f_0(t)*\delta_T(t)]=F_0(s)\red{\frac{1}{1-e^{-sT}}}
$$
我们将 $\red{\dfrac{1}{1-e^{-sT}}}$ 称为周期化因子。
时域微分
双边
\[\L[\frac{\dif x(t)}{\dif t}]=s X(s)\]证明
单边
\[\L[\frac{\dif x(t)}{\dif t}]=s X(s)-x(0_-)\]证明
补充:n次单边微分
\[\frac{\dif x^n(t)}{\dif^n t} \xleftrightarrow{\L} s^n F(s)-\sum_{r=0}^{n-1} s^{n-r-1} x^{(r)}(0_-)\]时域积分
双边
\[\int_{-\infty}^t x(\tau)\dif \tau \xleftrightarrow{\L} \frac{X(s)}{s}\]证明
单边
\[\int_{-\infty}^t x(\tau)\dif \tau \xleftrightarrow{\L} \frac{X(s)}{s}+\frac{f^{(-1)}(0_-)}{s}\]证明
初值定理
前提:$x(t)$,$\dfrac{\dif f(t)}{\dif t}$ 可以进行拉氏变换,则
\[\lim_{t\rightarrow 0_+} x(t)=x(0_+)=\lim_{s\rightarrow \infty} sX(s)\]若 $X(s)$ 不是真分式,那么应化为真分式+多项式 $X(s)=X_1(s)+\cdots+k_1s+k_0$,从而:
\[x(0_+)=\lim_{s\rightarrow\infty} sF_1(s)\]这是因为:
\[k_0\delta(t)+k_1\delta'(t)+\cdots \xleftrightarrow{\L} k_0+k_1s+\cdots\\ 记为:x_2(t) \xleftrightarrow{\L} X_2(s)\\ 显然,x_2(0_+)=0\\ 但是 \lim_{s\rightarrow \infty} sX_2(s) =\infty\]证明
由时域微分性质:
\[\int_{0_-}^{+\infty} \frac{\dif x(t)}{\dif t} e^{-st} \dif t=s X(s)-x(0_-)\]把 $0-$ 换为 $0+$:
\[\int_{0_+}^{+\infty} \frac{\dif x(t)}{\dif t} e^{-st} \dif t=s X(s)-x(0_+)\]对左边 s 取极限:
\[\lim_{s\rightarrow\infty} \left[ \int_{0_+}^{+\infty} \frac{\dif x(t)}{\dif t} e^{-st} \dif t \right] =\int_{0_+}^{+\infty} \frac{\dif x(t)}{\dif t} \lim_{s\rightarrow\infty} \left[ e^{-st}\right] \dif t = 0\]从而:
\[\lim_{s\rightarrow X(s)s}-x(0_+)=0\\ \lim_{s\rightarrow X(s)s}=x(0_+)\]终值定理
前提:$x(t)$,$\dfrac{\dif f(t)}{\dif t}$ 可以进行拉氏变换,则
\[\lim_{t\rightarrow \infty} x(t)=x(\infty)=\lim_{s\rightarrow 0} sX(s)\]证明
根据初值定理证明中得到的公式
\[\int_{0_+}^{+\infty} \frac{\dif x(t)}{\dif t} e^{-st} \dif t=s X(s)-x(0_+)\\ s X(s)=x(0_+)+\int_{0_+}^{+\infty} \frac{\dif x(t)}{\dif t} e^{-st} \dif t\]对左右两边令 s 趋于 0:
\[\lim_{s\rightarrow 0} sX(s)=x(0_+)+ \lim_{s\rightarrow 0} \int_{0_+}^{+\infty} \frac{\dif x(t)}{\dif t} e^{-st} \dif t\\ =x(0_+)+\lim_{t \rightarrow \infty} x(t)-x(t_+)\\ =\lim_{t \rightarrow \infty} x(t)\]终值存在,只可能满足如下任一情况:
- 极点都在左半平面,终值为 0
- 单极点在 $s=0$,终值等于分式展开式中 $\frac{k}{s}$ 项的系数 $k$
s域微分
\[\L [tx(t)]=-\frac{\dif X(s)}{\dif s}\\ \L [t^n x(t)]=(-1)^n \frac{\dif ^n X(s)}{\dif s^n}\]证明
s域积分
\[\L [\frac{x(t)}{t}]=\int_s^{\infty} X(\lambda) \dif \lambda\\ 要求 \lim_{t\rightarrow 0} \frac{x(t)}{t} 有界\]证明
总结
拉式变换与傅里叶变换的关系
- 收敛轴位于 s 平面的右半平面,收敛域不包含虚轴,则 $F(j\omega)$ 不存在
- 收敛轴位于 s 平面的左半平面,则 $F(j\omega)=F(s) \Big\vert_{s=j\omega}$
- 收敛轴位于虚轴,则 $F(j\omega)=F(s)\vert_{s=j\omega}+\pi \sum_{n} k_n \delta(\omega-\omega_n)$