拉普拉斯变换分析

$\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \newcommand{\L}{\mathcal{L}} \newcommand{\ft}{\xleftrightarrow{\F}} \newcommand{\red}[1]{\color{orangered}{#1}}$

下面来讨论如何利用拉普拉斯分析系统。

系统函数

系统函数一般有如下形式：

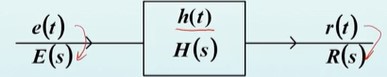
批注 2020-06-02 101136

时域上，$r(t)=e(t)*h(t)$，根据拉氏变换的卷积性质，有 $R(s)=E(s)\cdot H(s)$，所以：

\[H(s)=\frac{R(s)}{E(s)}=\frac{零状态响应拉氏变换}{激励信号拉氏变换}\]

如果系统由微分方程表征：

\[\sum_{k=0}^n a_k \frac{\dif^k r(t)}{\dif t^k} = \sum_{j=0}^m b_j \frac{\dif^j e(t)}{\dif t^j}\]

对两边取拉氏变换，可以得到LCCDE描述的系统函数：

\[\sum_{k=0}^n a_k s^k R(s) = \sum_{j=0}^m b_j s^j E(s)\\ H(s)=\frac{R(s)}{E(s)}=\frac{\sum_{j=0}^m b_j s^j}{\sum_{k=0}^n a_k s^k}\]

我们可以将系统函数改写为：

\[H(s)=\frac{B(s)}{A(s)}=K\frac{\prod_{j=1}^m (s-z_j)}{\prod_{k=1}^n (s-p_k)}\]

从而可以得到系统的零点 $z_i$、极点 $p_i$ 和零极点图。

系统联结

LTI系统并联：

\[H(s)=H_1(s)+H_2(s)\\ \rm{ROC}=R_1\cup R_2\]

LTI系统串联：

\[H(s)=H_1(s)H_2(s)\\ \rm{ROC}=R_1\cup R_2\]

LTI系统反馈：

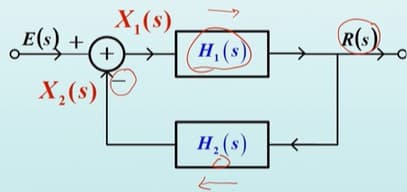
批注 2020-06-02 104736

\[\begin{cases} X_1(s)=E(s)-X_2(s)\\ R(s)=X_1(s)H_1(s)\\ X_2(s)=R(s)H_2(s) \end{cases}\\ \Rightarrow H(s)=\frac{H_1(s)}{1+H_1(s)H_2(s)}\]

系统因果性

要求收敛域在收敛轴的右端（右边信号）

系统稳定性

之前说过，稳定性指：有界输入得到有界输出（BIBO）。系统稳定，则必须满足如下充要条件：

\[绝对可积条件：\int_{-\infty}^{+\infty} |h(t)|\dif t\leq M\]

证明

\[充分性：设输入有界\;|e(t)|\leq M_e，则响应为：\\ \begin{align} |r(t)|&=|\int_{-\infty}^{+\infty}h(\tau)e(t-\tau)\dif \tau|\\ &\leq\int_{-\infty}^{+\infty}|h(\tau)|\cdot |e(t-\tau)|\dif \tau\\ &\leq M_e \int_{-\infty}^{+\infty}|h(\tau)|\cdot \dif \tau\\ &\leq M_e M_h \end{align}\\\]

\[必要性：若 \int_{-\infty}^{+\infty} |h(t)|\dif t 无界，则可构造有界输入信号：\\ e(-t)=\begin{cases} -1 & h(t)<0\\ 1 & h(t)\geq 0 \end{cases}\\ 则 e(-t)h(t)=|h(t)|\\ r(0)=\int_{-\infty}^{+\infty}h(\tau)e(-\tau)\dif \tau = \int_{-\infty}^{+\infty} |h(\tau)| \dif \tau\\ \therefore 存在有界信号使得 r(0) 无界\]

在时域上，系统稳定性可以通过 $\int_{-\infty}^{+\infty} \vert h(t)\vert \dif t\leq M$ 判定，对应在 s域要满足：$H(s)$ 的收敛域包含虚轴。如果再要求系统是因果的，则要满足：极点位于左半平面。我们可以通过单位冲激响应来验证这个结论：

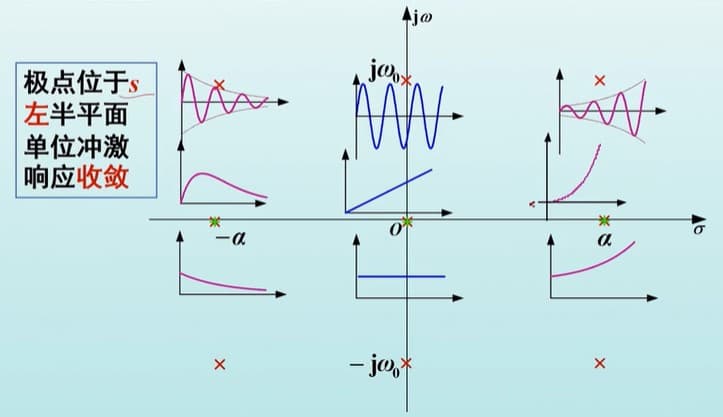
批注 2020-06-02 115425

因果系统稳定性判定方法：

稳定系统：全部极点位于左半平面（不含虚轴），$\lim_{t\rightarrow\infty}h(t)=0$
不稳定系统：极点位于右半平面，或虚轴上有二阶或以上极点，$\lim_{t\rightarrow\infty}h(t)\rightarrow \infty$
临界稳定（不稳定）系统：极点位于虚轴，且只有一阶，$\lim_{t\rightarrow\infty}h(t)$ 为非零数值或等幅振荡。

零极点与波形特征

下面用几张gif图来说明系统零极点与 $h(t)$ 的关系。

MATLAB 代码

参考：https://www.jianshu.com/p/cd9501bc810a

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
clc;clear;close all;
k=1;
for i = [-0.5:0.1:0 0.2:0.2:0.8]
    set(gcf,'Position',[0,0,500,250], 'color','w');
    b=1; %分子
    a=[1 i]; %分母
    sys=tf(b,a); %构造s域表达式
    subplot(121)
    pzmap(sys) %画 poles zeros map
    axis([-1 1 -1 1])
    subplot(122)
    impulse(b,a) %画 h(t)
    axis([-1 3 -1 5])

    %制作gif
    if i == -0.5
        %首帧，设置样式和大小
        frame = getframe(gcf); % 获取整个窗口内容的图像
        im=frame2im(frame);
        [I{k},map{k}]=rgb2ind(im,8);
        imwrite(I{k},map{k},'1.gif','gif','Loopcount',Inf,'DelayTime',0.4);
    else
        frame = getframe(gcf);% 获取整个窗口内容的图像
        im=frame2im(frame);
        [I{k},map{k}]=rgb2ind(im,8);
        %追加模式
        imwrite(I{k},map{k},'1.gif','gif','WriteMode','append','DelayTime',0.2);
    end
    k=k+1;
end

for i = (k-1):-1:1
    imwrite(I{i},map{i},'1.gif','gif','WriteMode','append','DelayTime',0.2);
end

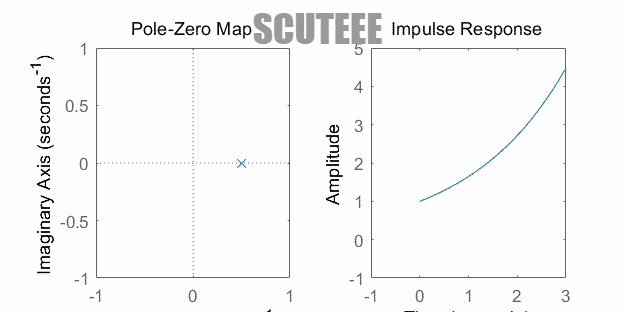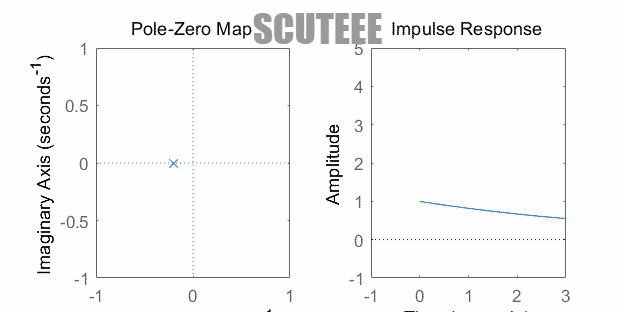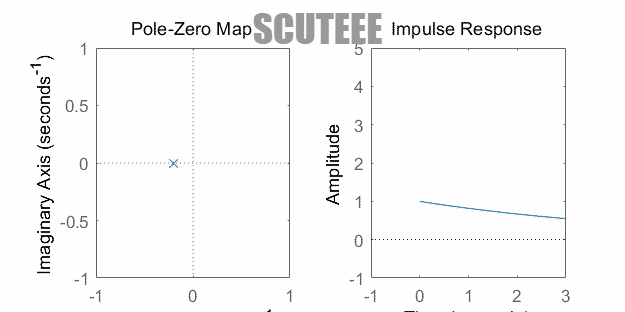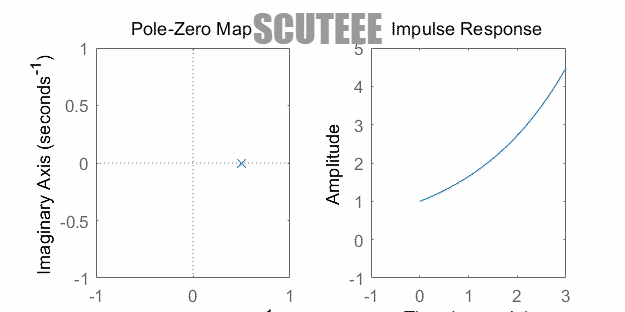
$H(s)=\dfrac{1}{s+\alpha} \xleftrightarrow{\L} h(t)=e^{-\alpha t}u(t)$
极点在左实轴 ↔ $h(t)$ 衰减
极点在原点 ↔ $h(t)$ 等幅
极点在右实轴 ↔ $h(t)$ 增长

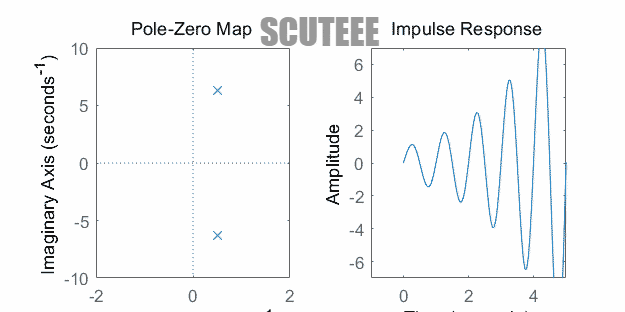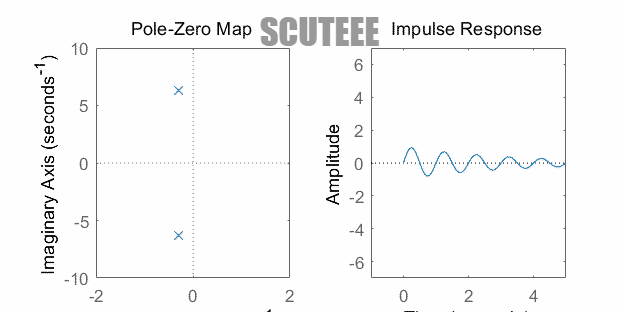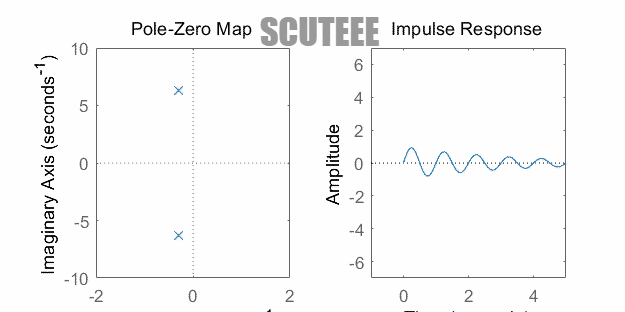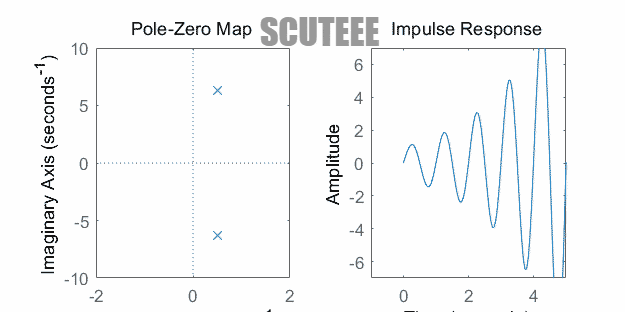
$H(s)=\dfrac{\omega_0}{(s+\alpha)^2+\omega_0^2} \xleftrightarrow{\L} h(t)=e^{-\alpha t}\sin(\omega_0 t)u(t)$
极点在左半平面 ↔ $h(t)$ 衰减振荡
极点在虚轴 ↔ $h(t)$ 等幅振荡
极点在右半平面 ↔ $h(t)$ 增长振荡

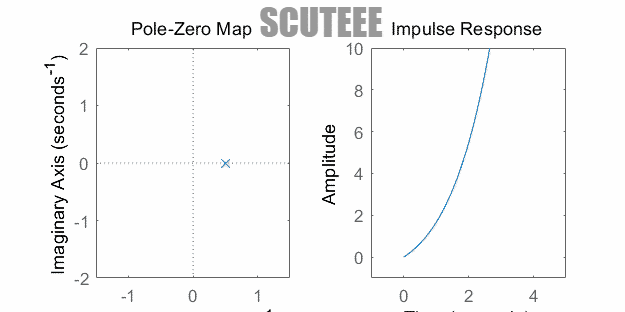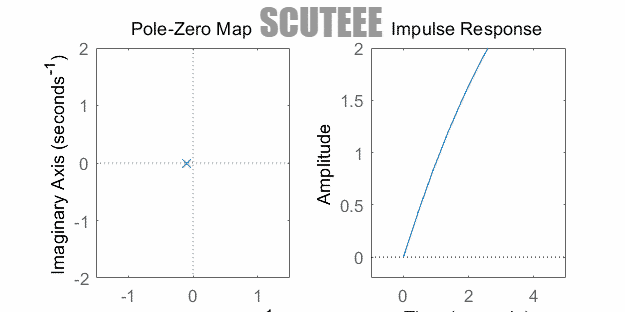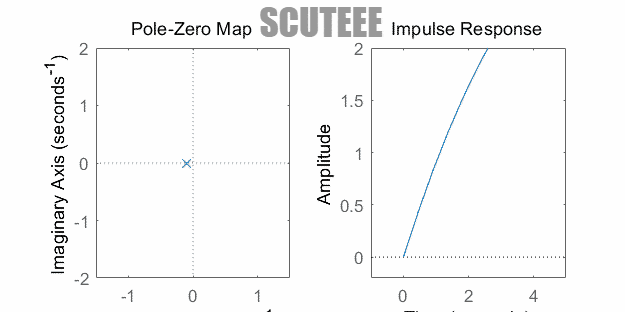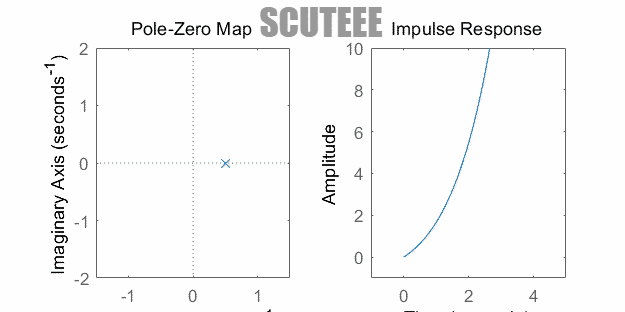
注：图中为二重极点
$H(s)=\dfrac{1}{(s+\alpha)^2} \xleftrightarrow{\L} h(t)=te^{-\alpha t}u(t)$
极点在左实轴 ↔ $h(t)$ 衰减
极点在原点 ↔ $h(t)$ 线性增长
极点在右实轴 ↔ $h(t)$ 增长

信号、系统的极点与响应的关系

设激励为 $e(t)$，系统为 $h(t)$，对应的拉氏变换为：$E(s)=\dfrac{A_E(s)}{\prod_{i=1}^m (s-q_i)}$，$H(s)=\dfrac{A_H(s)}{\prod_{i=1}^n (s-p_i)}$

\[\begin{align} 零状态响应：R(s)&=E(s)H(s)\\ &=\dfrac{A_E(s)}{\prod_{i=1}^m (s-q_i)}\cdot \dfrac{A_H(s)}{\prod_{i=1}^n (s-p_i)}\\ &=\sum_{i=1}^m \frac{X_i}{s-q_i}+\sum_{=1}^n \frac{Y_i}{s-p_i}\\ &=强迫响应+自由响应 \end{align}\]

系统的极点 $p_i$ 称为 自然频率 或 固有频率。

系统的频率响应

前提：系统是因果稳定系统（极点全部位于左半平面，收敛域包括虚轴）

假设输入信号为 $e(t)=E_m \sin (\omega_0 t)$，$E(s)=\frac{E_m\omega_0}{s^2+\omega_0^2}$，则响应为：

\[\begin{align} R(s)&=\frac{E_m \omega_0}{s^2 + \omega_0^2}\cdot H(s)\\ &=\frac{K_{-j\omega_0}}{s+j\omega}+\frac{K_{j\omega_0}}{s-j\omega_0}+\frac{K_1}{s-p_1}+\cdots+\frac{K_n}{s-p_n}\\ \end{align}\]

对于稳定系统，其系统函数 $h(t)$ 是随时间衰减，如果要求稳态响应，只要求前两项。先求系数：

\[K_{-j\omega_0}=(s+j\omega_0)R(s)\Big\vert_{s=-j\omega_0}=\frac{E_m\omega_0H(-j\omega_0)}{-2j\omega_0}\]

由于 $h(t)$ 是实函数，所以 $H(-j\omega_0)=H^*(j\omega_0)=H_0 e^{-j\phi_0}$（写成幅度与角度的形式），代入上式：

\[K(-j\omega_0)=\frac{E_mH_0 e^{-j\phi_0}}{-2j}\\ 同理，K(j\omega_0)=\frac{E_m H_0 e^{j\phi_0}}{2j}\]

所以稳态响应为：

\[R_{ss}(s)=\frac{E_mH_0}{2j}(-\frac{e^{-j\phi_0}}{s+j\omega_0}+\frac{e^{j\phi_0}}{s-j\omega})\\ \begin{align} r_{ss}(t)&=\frac{E_mH_0}{2j}(-e^{-j\phi_0}e^{-j\omega_0t}+e^{j\phi_0}e^{j\omega_0 t})\\ &=E_m H_0 \sin (\omega_0 t+\phi_0) \end{align}\]

由零、极点确定频率响应

系统函数写成零、极点的形式就是：

\[H(s)=K\frac{\prod_{i=1}^m(s-z_i)}{\prod_{i=1}^n (s-p_i)}\\ H(j\omega)=K\frac{\prod_{i=1}^m(j\omega-z_i)}{\prod_{i=1}^n (j\omega-p_i)}\]

我们将分子、分母写成如下形式：

\[\begin{cases} j\omega-z_j=N_j e^{j\psi_j}\\ j\omega-p_i=M_i e^{j\theta_i} \end{cases}\\ H(j\omega)=K\frac{\prod_{i=1}^m N_i e^{j\psi_i}}{\prod_{i=1}^n M_i e^{j\theta_i}}\\ \therefore |H(j\omega)|=K\frac{N_1\cdots N_m}{M_1\cdots M_n} \quad \varphi(\omega)=\sum_{i=1}^m \psi_i - \sum_{i=1}^m \theta_i\\\]

下面来说明如何在零、极点图上找出 $N_i$,$M_i$,$\psi_i$,$\theta_i$。以零点为例：$j\omega - z_j = N_j e^{j\psi_j}$，而 $z_j$ 是零点，可以在图中找到；$j\omega$ 是频率，可以由我们给定的。因此，由矢量运算，可以得到下图：

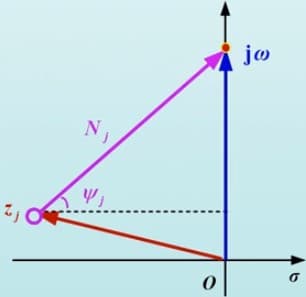
可见，只需要将零点（或极点）与虚轴上的特点频率点连接，就能得到 $N_i$,$M_i$,$\psi_i$,$\theta_i$。故我们可以从图中定性地得到频率响应特性，用下面例题来说明。

例题：已知电容的 s域模型为 $\frac{1}{sC}$，电阻的 s域模型为 $R$，现将一个电容、一个电阻串联，输入电压 $V_1(s)$，电阻上输出电压 $V_2(s)$。分析频率响应特性。

解：$H(s)=\dfrac{V_2(s)}{V_1(s)}=\dfrac{s}{s+\frac{1}{RC}}$，$H(j\omega)=\dfrac{V_2(j\omega)}{V_1(j\omega)}=\dfrac{j\omega}{j\omega+\frac{1}{RC}}$
作出零极点图：

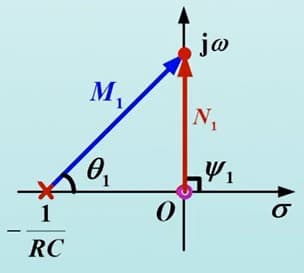
而 $\vert H(j\omega) \vert = \frac{N_1}{M_1}$，从图中可以看出，当 $\omega$ 趋近于 0 时，$N_1 \ll M_1$，$\vert H(j\omega) \vert\approx 0$；随着 $\omega$ 增加，$N_1 \approx M_1$，$\vert H(j\omega) \vert\approx 1$。所以这是个高通滤波电路。
$$ \vert H(j\omega) \vert = \frac{N_1}{M_1} =\frac{\omega}{\sqrt{\omega^2+(\frac{1}{RC})^2}} $$

上篇拉普拉斯变换

下篇z变换