\(\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \newcommand{\Z}{\mathcal{Z}} \newcommand{\ft}{\xleftrightarrow{\F}} \newcommand{\red}[1]{\color{orangered}{#1}}\)
利用 z变换求差分方程
根据单边z变换的移位性质 $\Z[x(n-m)u(n)]=z^{-m} [X(z)+\sum_{k=-m}^{-1} x(k)z^{-k}]$,得到 z变换方程,进而求得 $Y(z)$,然后再由反变换得到 $y(n)$
已知系统的差分方程表达式位 $y(n)-0.9y(n-1)=x(n)$,$x(n)=0.05u(n)$,若起始状态为 $y(-1)=1$,求 $y(n)$。
解:对方程作单边 z变换:
$$
Y(z)-0.9[z^{-1}Y(z)+y(-1)]=X(z)\\
Y(z)=\frac{X(z)+0.9y(-1)}{1-0.9z^{-1}}
$$
代入已知条件:
$$
\begin{align}
Y(z)&=\frac{0.05z^2}{(z-1)(z-0.9)}+\frac{0.9y(-1)z}{z-0.9}\\
&=\frac{0.5z}{z-1}+\frac{0.45z}{z-0.9}
\end{align}
$$
再做反变换,得到 $y(n)=0.5+0.45\times(0.9)^n$,$n\geq 0$
观察上面例题中的 $Y(z)$,可以认为 $Y(z)$ 由 $\frac{0.05z^2}{(z-1)(z-0.9)}$ 和 $\frac{0.9y(-1)z}{z-0.9}$ 两部分组成。第一项称为 零状态响应,第二项称为 零输入响应。
而经过分式展开,$Y(z)$ 又可以分为 $\frac{0.5z}{z-1}$ 和 $\frac{0.45z}{z-0.9}$ 两部分。第一项极点在单位圆上,称为 稳态响应(在圆外也属于稳态响应),第二项极点在单位圆内部,称为 暂态响应(衰减)。
进一步考虑稳态响应与暂态响应,可以发现稳态响应的极点来源于信号,我们将来源于信号的极点称为 强迫响应,来源于系统极点称为 自由响应。(如果既来自于系统,也来自于信号,则优先考虑系统,算作自由响应)
总结一下:
- 按有无输入分:零状态、零输入
- 按极点位置分:稳态、暂态
- 按极点来源分:强迫、自由
求系统函数
离散系统的差分方程为:
\[\sum_{k=0}^N a_k y(n-k)=\sum_{r=0}^M b_r x(n-r)\]两端取双边 z 变换,根据双边移位性质:
\[\sum_{k=0}^N a_k z^{-k}Y(z)=\sum_{r=0}^M b_r z^{-r} X(z)\]从而得到系统函数为:
\[H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{r=0}^M b_r z^{-r}}{\sum_{k=0}^N a_k z^{-k}}\]- 并联:$H(z)=H_1(z)+H_2(z)$
- 级联:$H(z)=H_1(z)\cdot H_2(z)$
写成零、极点的形式:
\[H(z)=\frac{\sum_{r=0}^M b_r z^{-r}}{\sum_{k=0}^N a_k z^{-k}}=G\frac{\prod_{r=1}^M (1-z_rz^{-1})}{\prod_{k=1}^N (1-p_k z^{-1})}\]展开成部分分式形式:
\[H(z)=\sum_{k=0}^N \frac{A_k z}{z-p_k}\\ \Rightarrow h(n)=\sum_{k=0}^N A_k (p_k)^n u(n)\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
clc;clear;close all;
k=1;
for i = [-1.5:0.1:-1 -0.8:0.2:1 1.1:0.1:1.5]
set(gcf,'Position',[0,0,800,300], 'color','w');
Z=[];%零点
P=[i]; %极点
K=1; % 系数K
[b,a]=zp2tf(Z,P,K); %获得分式表达式
% sys=tf(b,a); %构造z域表达式
subplot(121);
zplane(b,a); %画z平面的零极点图
axis([-1.5 1.5 -1.5 1.5]);
legend('零点','极点');
title('零极点分布图');
subplot(122);
impz(b,a,20); %画 h(t)
grid on;
%制作gif
if i == -1.5
%首帧,设置样式和大小
frame = getframe(gcf); % 获取整个窗口内容的图像
im=frame2im(frame);
[I{k},map{k}]=rgb2ind(im,8);
imwrite(I{k},map{k},'1.gif','gif','Loopcount',Inf,'DelayTime',0.8);
else
frame = getframe(gcf);% 获取整个窗口内容的图像
im=frame2im(frame);
[I{k},map{k}]=rgb2ind(im,8);
%追加模式
imwrite(I{k},map{k},'1.gif','gif','WriteMode','append','DelayTime',0.4);
end
k=k+1;
end
for i = (k-1):-1:1
imwrite(I{i},map{i},'1.gif','gif','WriteMode','append','DelayTime',0.4);
end
一阶系统
\[H(z)=\frac{z}{z-a}\\ h(n)=a^n u(n)\]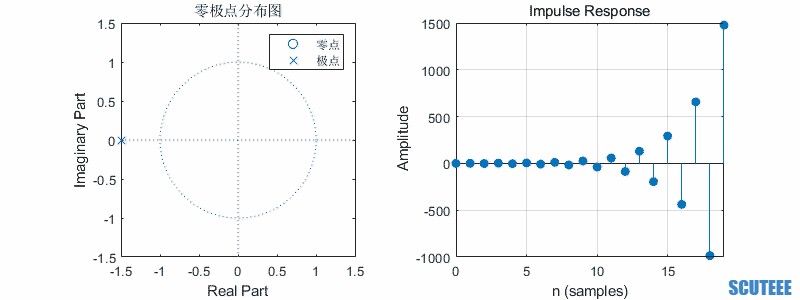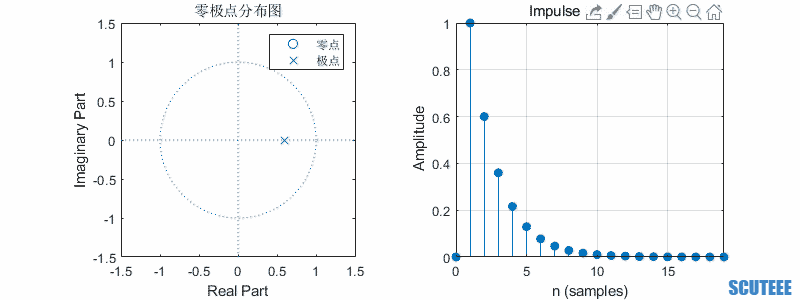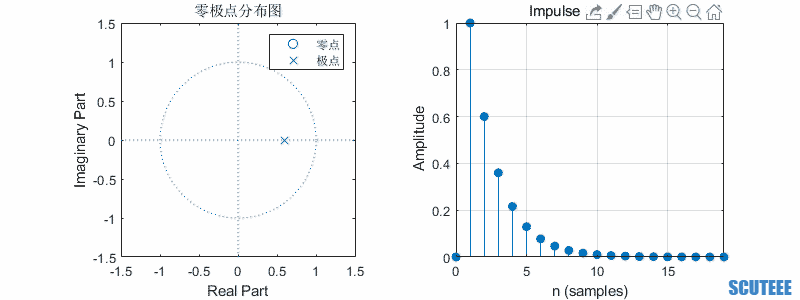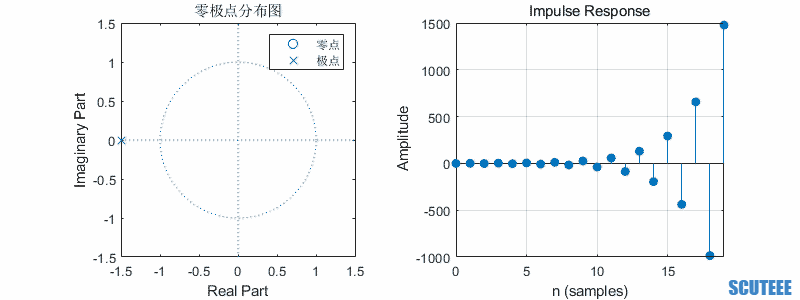
- 极点在圆内,收敛
- 极点在圆上,等幅
- 极点在圆外,增长
二阶系统
\[H(z)=\frac{1}{2}(\frac{z}{z-\beta e^{j\omega}}+\frac{z}{z-\beta e^{-j\omega}})=\frac{z(z-\beta \cos\omega)}{(z-\beta e^{j\omega})(z-\beta e^{-j\omega})}\\ h(n)=\frac{1}{2}(\beta e^{j\omega})^n u(n)+\frac{1}{2}(\beta e^{-j\omega})^n u(n)=\beta^n \cos(\omega n) u(n)\]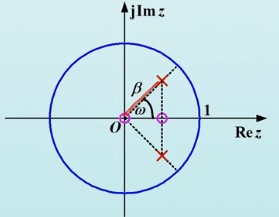
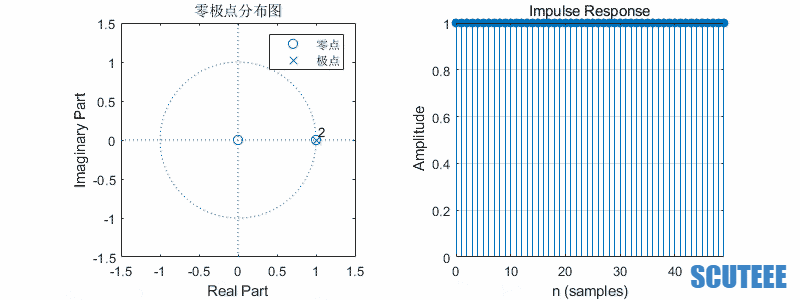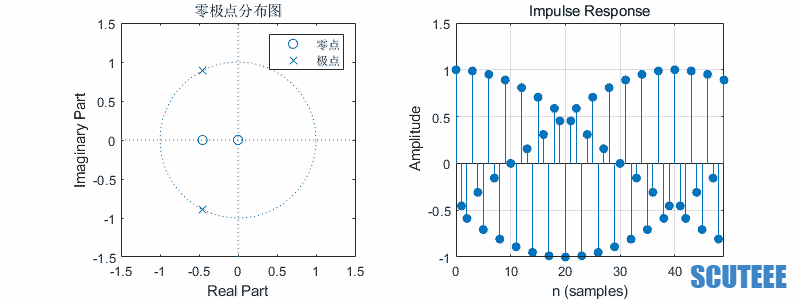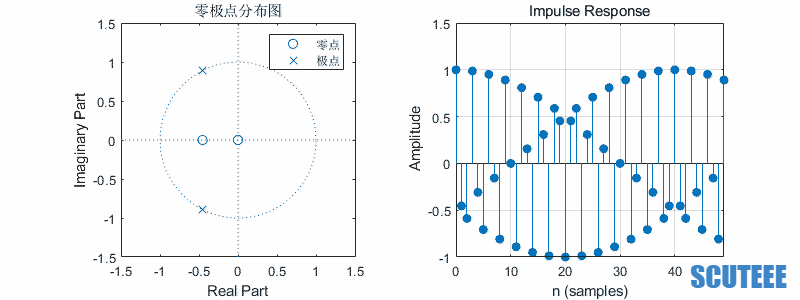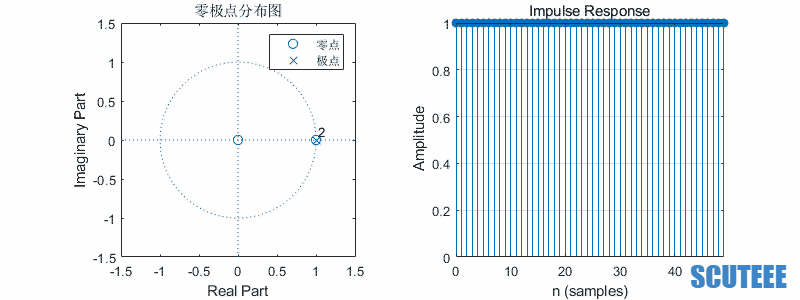
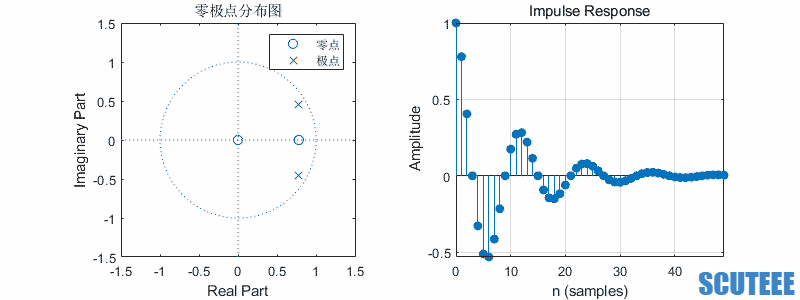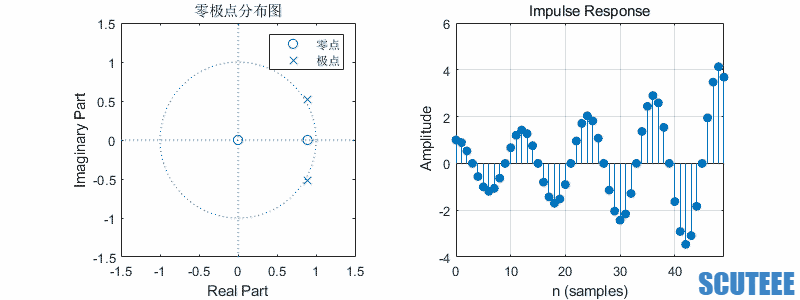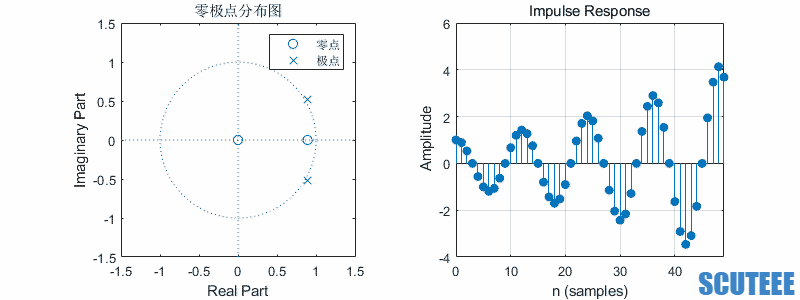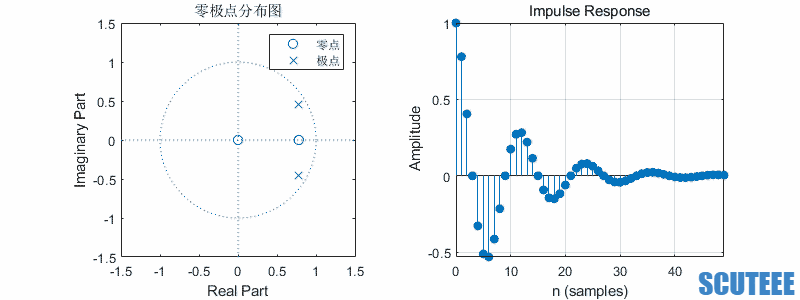
- $\omega$ 决定频率,$\beta$ 决定幅度
- 圆上,等幅
- 圆内,收敛
- 圆外,发散
s 与 z 的映射关系
- 前面引入 z变换时定义了 $z=e^{sT}$($T$ 是采样周期)
- 令 $s=\sigma+j\Omega$,$z=re^{j\omega}$
- 则 $r=e^{\sigma T}$,$\omega=\Omega T=\Omega\dfrac{2\pi}{\Omega_s}$
- 映射关系:
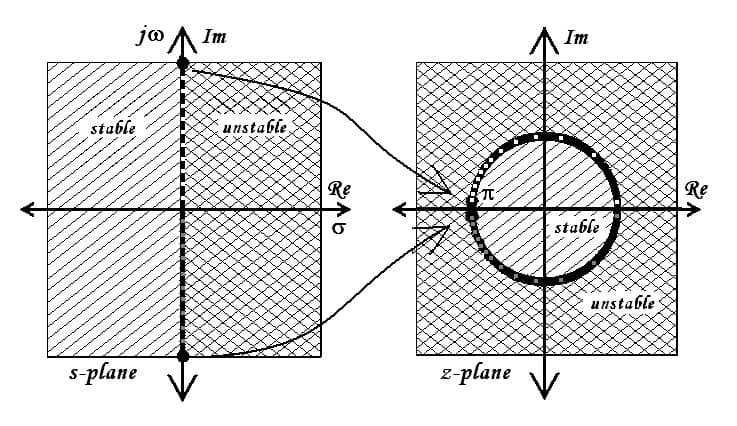
- $s$ 平面上的每条竖线对应于 $z$ 平面上的一个圆
- $s$ 平面上的每条横线对应于 $z$ 平面上的一条从原点出发的射线
- $s$ 左半平面对应 $z$ 平面单位圆内,右半平面对应单位圆外,虚轴对应单位圆
因果性
因果信号意味着:$h(n)=h(n)u(n)$,对应于 $z$ 域则是收敛域在某个圆外并包含无穷远。
稳定性
| 在时域上要求:$\sum_{n=-\infty}^{\infty} | h(n) | <\infty$;在 z域则要求收敛域包含单位圆,即全部极点落在单位圆内。 |