判断以下结论的对错,要求给出分析过程:
1. 两个周期信号相加依然是周期信号?
2. 非周期信号一定是能量信号?
3. 能量信号一定是非周期信号?
4. 两个功率信号相加依然是功率信号?
5. 两个功率信号之积依然是功率信号?
6. 能量信号乘功率信号之积是能量信号?
7. 随机信号一定是非周期信号?
1. 两个周期信号相加依然是周期信号(×)
设周期信号 $x_1(t)=x_1(t+M)$,$x_2(t)=x_2(t+N)$
令 $x(t)=x_1(t)+x_2(t)$
要使 $x(t)=x(t+k)$,则要求 $k$ 是 $M,N$ 的(最小)公倍数。
即存在正整数 $P,Q$,使得 $k=QM=PN$,也就是要求:$\frac{M}{N}=\frac{P}{Q}$ 必须是有理数。显然当 $M,N$ 一个有理,一个无理时,相加后无周期。
更多讨论可以看 知乎:如果 f(x) 与 g(x) 均为周期函数,判断其相加后的周期性?
但在实际工程中,我们一般会将周期近似为有限位小数,所以我们可以认为,两个周期信号相加是 概周期信号。
2. 非周期信号一定是能量信号(×)
考虑阶跃信号。
3. 能量信号一定是非周期信号(√)
周期信号能量一定无穷大,即一定是功率信号;而功率信号不可能是周期信号。所以周期信号一定不是能量信号,从而逆否命题:【能量信号一定是非周期信号】成立。(由于零信号无意义且无周期,我们不考虑零信号)。
4. 两个功率信号相加依然是功率信号(×)
一正一反相消。
5. 两个功率信号之积依然是功率信号(×)
一个是阶跃信号,一个是阶跃信号以y轴对称的信号,相乘为零。
6. 能量信号乘功率信号之积是能量信号(×)
emm……其实这个挺难想的。给出如下反例:
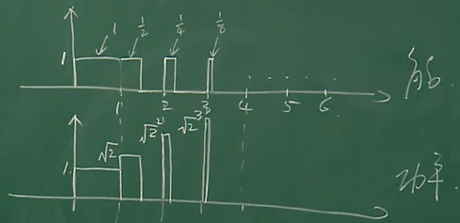
能量信号:$x_1(t)=\sum_{k=0}^\infty [u(x-k)-u(x-\sum_{n=1}^k\frac{1}{2^n})]$ 级数收敛;
功率信号:$x_2(t)=\sum_{k=0}^\infty \sqrt{2}^k[u(x-k)-u(x-\sum_{n=1}^k\frac{1}{2^n})]$,级数发散;
相乘后依然是 $x_2(t)$,是功率信号。
7. 随机信号一定是非周期信号(×)
只要不能写出确定的函数式,则是随机信号。
比如:$\sin(x+H)$,其中,$H$ 是随机的。
显然上面的函数的周期为 $2\pi$,是周期信号,但我们无法画出这个信号。