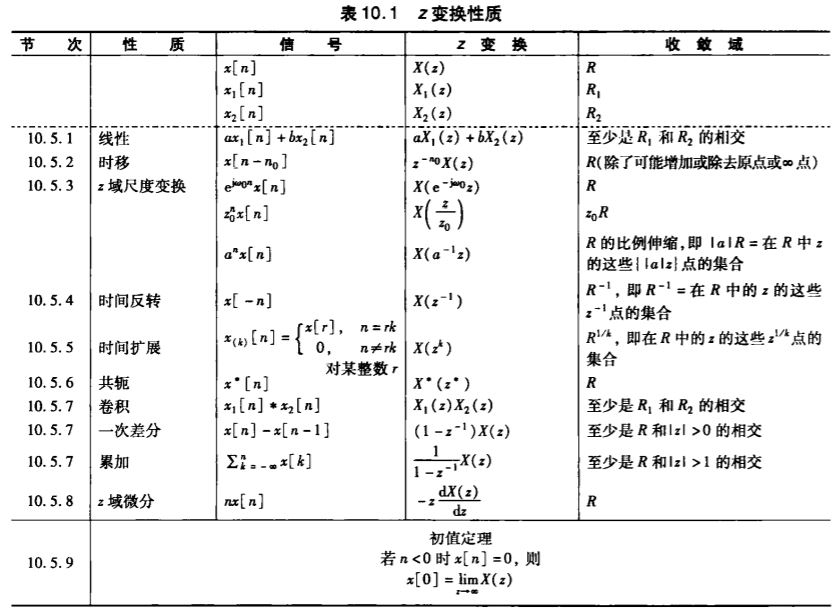
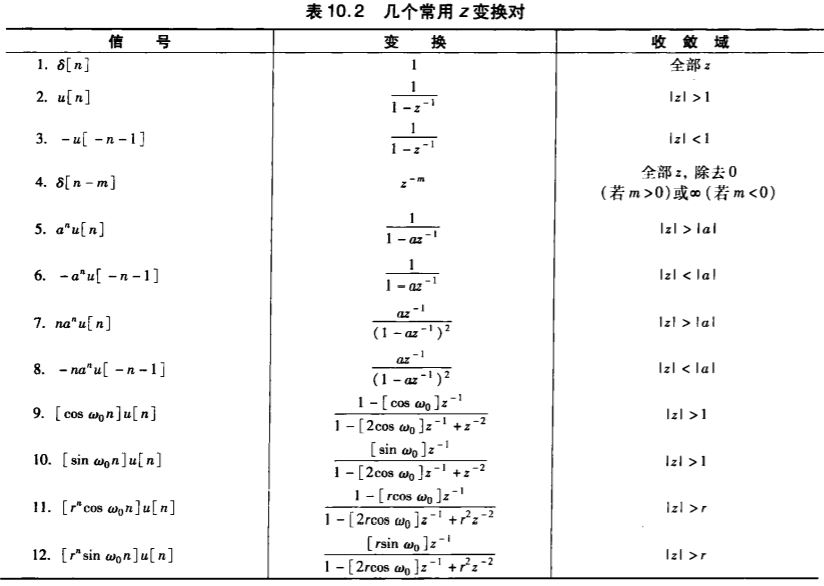
\(\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \newcommand{\L}{\mathcal{L}} \newcommand{\Z}{\mathcal{Z}} \newcommand{\ft}{\xleftrightarrow{\F}} \newcommand{\red}[1]{\color{orangered}{#1}}\)
z变换的引入
我们考虑抽样信号的拉氏变换:
\[\begin{align} x_s(t)&=x(t)\cdot \delta_T(t)\\ &=x(t)\sum_{n=-\infty}^{\infty} \delta(t-nT)\\ &=\sum_{n=-\infty}^{\infty} x(nT) \delta(t-nT) \end{align}\\\]由于 $\L[\delta(t)]=1$,由时移性质,得到 $\L[\delta(t-nT)]=e^{-snT}$,故:
\[\begin{align} X_s(t)&=\L[x_s(t)]=\sum_{n=-\infty}^{\infty} x(nT) e^{-snT} \end{align}\]令 $z=e^{sT}$,$x[n]=x_s(nT)$,则:
\[X(z)=\sum_{n=-\infty}^{\infty} x[n]z^{-n}\]这个就是 $z$ 变换,更准确来讲是 双边 $z$ 变换,其中,$-\infty<n\leq1$ 部分是左边序列,$0\leq n<+\infty$ 是右边序列。相应的,也有单边变换:
\[X(z)=\sum_{n=0}^{\infty} x[n]z^{-n}\]收敛域
令 $X(z)$ 收敛的 $z$ 的集合称为 收敛域 ROC,计算 z变换时必须写出收敛域。根据级数收敛的相关定理,我们知道要让
常见 z 变换
单位函数
\[\L[\delta(n)]=\sum_{n=-\infty}^{\infty} \delta[n]z^{-n}= \delta(0)z^0=1\]收敛域为整个 z 平面。
有限长序列
\[X(z)=\sum_{n=n_1}^{n_2} x[n]z^{-n}\]为了使讨论具有普遍性,取 $n=[-2,2]$,则:
\[\begin{align} X(z)&=x(-2)z^{2}+x(-1)z^{1} &|z|\neq\infty\\ &+x(0)z^0 & 常数\\ &+x(1) z^{-1}+x(2)z^{-2} &|z|\neq 0 \end{align}\]所以收敛域为 $0<\vert z \vert<\infty$
单位阶跃序列
\[\begin{align} X(z)&=\sum_{n=-\infty}^{+\infty} u[n]z^{-n}\\ &=1+z^{-1}+z^{-2}+\cdots\\ &= \frac{1-z^{-\infty}}{1-z^{-1}} \end{align}\]当 $\vert z^{-1} \vert<1$ 时收敛于 $\frac{z}{z-1}$,故ROC为 $\vert z \vert >1$
斜变序列
\[x[n]=nu[n]\]根据单位阶跃的 z变换:
\[\sum_{n=0}^{+\infty} z^{-n} = \frac{1}{1-z^{-1}}\\ ROC: |z|>1\]两边求导:
\[\sum_{n=0}^{+\infty} n (z^{-1})^{n-1} = \frac{1}{(1-z^{-1})^{2}}\]两边同乘 $z^{-1}$:
\[\sum_{n=0}^{+\infty} n (z^{-1})^{n} = \frac{z^{-1}}{(1-z^{-1})^{2}}=\frac{z}{(z-1)^2}\]收敛域依然是 $\vert z \vert >1$
右边指数序列
\[x[n]=a^n u[n]\] \[X(z)=\sum_{0}^{+\infty} a^n z^{-n}=\sum_{n=0}^{+\infty} (\frac{a}{z})^n=\frac{1-(\frac{a}{z})^\infty}{1-\frac{a}{z}}\]当 $\vert \frac{a}{z} \vert <1$ 时,即 $\vert z \vert > \vert a \vert $ 时收敛于 $X(z)=\dfrac{1}{1-az^{-1}}=\dfrac{z}{z-a}$,故收敛域 ROC 为 $\vert z \vert > \vert a \vert $(圆外)
左边指数序列
\[x[n]=-a^n u[-n-1]=-(\cdots+a^{-2}+a^{-1})\\ (负号主要是为了导出后面的结论)\] \[\begin{align} X(z)&=-\sum_{n=-\infty}^{-1} a^n z^{-n}\\ {}^{m=-n}&=-\sum_{m=1}^{\infty} a^{-m} z^{m}\\ \end{align}\]当 $\vert a^{-1} z^m\vert<1$,即 $\vert z \vert < \vert a \vert$ 时收敛于 $X(z)=-\dfrac{za^{-1}}{1-za^{-1}}=\dfrac{z}{z-a}$,故收敛域为 $\vert z \vert < \vert a \vert$ (圆内),恰好与右边指数序列相反。
注意,左边指数与右边指数仅仅是 ROC 不同,而式子都相同。故已知 z变换时,我们需要 ROC 来确定是左边还是右边序列。
性质
下面用花体 $\Z$ 表示 Z 变换。为了方便区分括号,我们这里用 $x(n)$ 代替 $x[n]$
线性性
\[\Z[ax(n)+by(n)]=aX(z)+bY(z)\\ \text{ROC:取交集}\](证明略。)
例题:计算 $\Z[\sin(\omega_0 n)u(n)]$ 和 $\Z[\cos(\omega_0 n)u(n)]$
时移性
双边(参与变换的点数不变)
证明
由于单位时延对应的要乘上 $z^{-1}$,所以 $z^{-1}$ 在方框图中表示时延。
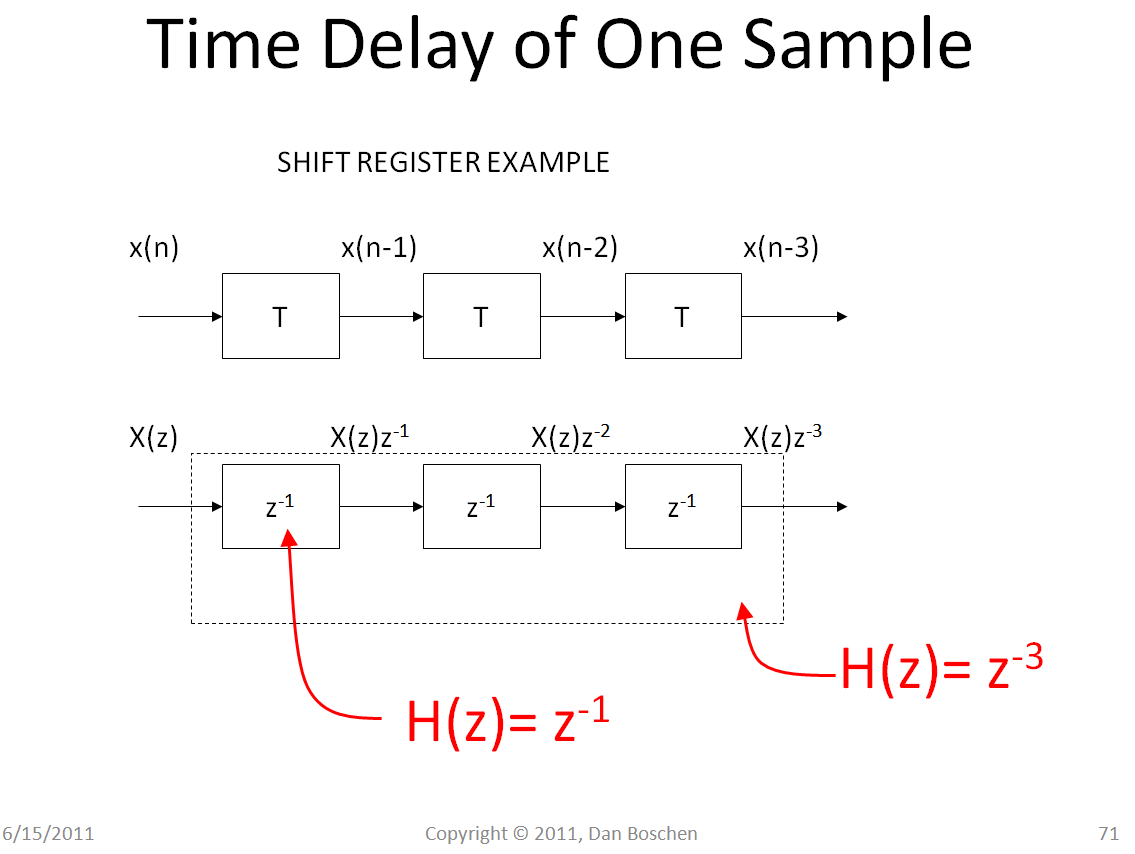
单边 (参与运算的点数增加或减少)
序列线性加权(z域微分)
\[nx(n) \leftrightarrow -z\frac{\dif X(z)}{\dif z}=z^{-1}\frac{\dif X(z)}{\dif z^{-1}}\]序列指数加权(z域尺度变换)
\[a^{n}x(n)\leftrightarrow X\left( \frac{z}{a} \right)\]证明
初值定理
若 $x(n)$ 为因果序列,则 $x(0)=\lim_{z\rightarrow \infty} X(z)$
证明
终值定理
若 $x(n)$ 为因果序列,并且 $x(\infty)$ 收敛(不包括振荡),则 $x(\infty)=\lim_{z\rightarrow 1} (z-1)X(z)$。
终值存在的条件:
- 极点位于单位圆内,$X(1)$ 处无极点,$x(\infty)=\lim_{z\rightarrow 1} (z-1)X(z)=0$
- 极点位于单位圆 $z=1$ 处,并且是一阶极点,$x(\infty)$ 对应于 $X(z)$ 展开式中,$\frac{z}{z-1}$ 项的系数。
证明
时域卷积定理
\[\Z[x(n)*h(n)]=X(z)\cdot H(z)\\ \text{ROC 取交集}\]证明 (还是老套路,交换求和顺序)
z域卷积定理(了解)
数字信号处理中会进一步学习。
\[\Z[x(n)h(n)]=\frac{1}{2\pi j} \oint_{c_1} X(\frac{z}{v}) H(v) v^{-1} \dif v\\ 或\;\Z[x(n)h(n)]=\frac{1}{2\pi j} \oint_{c_1} X(v) H(\frac{z}{v}) v^{-1} \dif v\\ 或设\; v=\rho e^{j\theta},\; z=re^{j\phi}\\ \Z[x(n)h(n)]=\frac{1}{2\pi} \int_{-\pi}^{+\pi} X(\rho e^{j\theta}) H(\frac{r}{\rho} e^{j(\phi-\theta)}) \dif \theta\]总结
逆z变换
部分分式展开法
\[X(z)=\frac{N(z)}{D(z)}=\frac{b_0+b_1 z + \cdots b_r z^r}{a_0+a_1 z+ \cdots a_k z^k}\]因果序列是右边序列,其收敛域是圆外,包括 $+\infty$,所以要求分母阶次大于分子,即 $k\geq r$。
常见信号的z变换:
| 信号 | z变换 | ROC |
|---|---|---|
| $\delta(n)$ | 1 | 整个平面 |
| $u(n)$ | $\dfrac{z}{z-1}$ | $\vert z \vert>1$ |
| $nu(n)$ | $\dfrac{z}{(z-1)^2}$ | $\vert z \vert>1$ |
| $a^n u(n)$ | $\dfrac{z}{z-a}$ | $\vert z \vert>\vert a \vert$ |
| $-a^n u(-n-1)$ | $\dfrac{z}{z-a}$ | $\vert z \vert<\vert a \vert$ |
注意到上面的z变换的分子都是 $z$,所以在求展开式时,可以先除以 $z$,然后像前面拉氏那样展开,然后再乘回 $z$:
\[\frac{X(z)}{z}=\sum_{i=1}^\infty \frac{A_i}{z-z_i}\\ \Rightarrow X(z)=\sum_{i=1}^\infty \frac{A_i z}{z-z_i}\]幂级数展开法
\[X(z)=\frac{N(z)}{D(z)}=\frac{b_0+b_1 z + \cdots b_r z^r}{a_0+a_1 z+ \cdots a_k z^k}\]可以利用长除法进行反变换(一般无法整除,只需写出前几项):
\[\begin{align} X(z)&=\sum_{n=-\infty}^{+\infty} x(n) z^{-n}\\ &= x(0)z^0 + x(1)z^{-1}+\cdots\\ &+ x(-1)z^1+x(-2)z^2+\cdots \end{align}\]这样就得到了 $x(n)$ 序列。
围线积分
\[X(z)=\sum_{n=0}^{\infty} x(n) z^{-n}\]选择一条逆时针方向的围线 $c$,使得 $X(z)z^{m-1}$ 的极点在 $c$ 的内部。对 $c$ 进行围线积分:
\[\frac{1}{2\pi j} \oint_c X(z) z^{m-1} \dif z=\frac{1}{2\pi j} \oint_c \left[ \sum_{n=0}^{\infty} x(n) z^{-n} \right] z^{m-1} \dif z\]交换积分与求和的顺序:
\[=\sum_{n=0}^\infty x(n) \left[ \frac{1}{2\pi j}\oint_c z^{-n+m-1} \red{\dif z} \right]\]令积分路径上的 $z=Re^{j\theta}$,$R$ 为常数:
\[=\sum_{n=0}^\infty x(n) \left[ \frac{1}{2\pi j}\int_{-\pi}^{+\pi} R^{m-n-1} e^{j(m-n-1)\theta} \red{jR e^{j\theta} \dif \theta} \right]\\ =\sum_{n=0}^\infty x(n) \left[ \frac{1}{2\pi } R^{m-n} \int_{-\pi}^{+\pi} e^{j(m-n)\theta} \dif \theta \right]\]因为:
\[\int_{-\pi}^{+\pi} e^{j(m-n)\theta} \dif \theta = \begin{cases} 2\pi & n=m\\ 0 & n \neq m \end{cases}\]所以:
\[= \begin{cases} x(n) & n=m\\ 0 & n \neq m \end{cases}\]经过推导可知 z反变换公式:
\[x(n)=\frac{1}{2\pi j} \oint_c X(z) z^{n-1} \dif z\]即:$x(n)=\dfrac{1}{2\pi j} \oint_c X(z) z^{n-1} \dif z$,根据留数定理:
\[x(n)=\sum \text{Res} [X(z) z^{n-1}] \Big\vert_{z=z_m}\]