\(\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \newcommand{\F}{\mathcal{F}} \newcommand{\ft}{\xleftrightarrow{\F}}\)
采样定理
如果一个信号是带限的1,并且它的样本取得足够密,则这些样本就能唯一地表征这一信号,并且能从样本中把信号恢复出来。
冲激串采样
设冲激串序列(pulse):
\[p(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT)\]则冲激串采样为:
\[x_p(t)=x(t)p(t)=\sum_{n=-\infty}^{+\infty} x(nT)\delta(t-nT)\]其中,$T$ 称为采样周期,$\omega_s=2\pi/T$ 称为采样频率(下标S 表示 Sampling)。
对 $x_p(t)$ 进行傅里叶变换(时域相乘对应频域卷积):
\[X_p(j\omega)=\frac{1}{2\pi}\int_{-\infty}^{+\infty} X(j\omega)P(j(\omega-\theta))\dif \theta\\ P(j\omega)=\frac{2\pi}{T}\sum_{k=-\infty}^{+\infty} \delta(\omega-k\omega_s)\]因为信号与冲激函数的卷积就是信号的移位,所以:
\[X_p(j\omega)=\frac{1}{T} \sum_{k=-\infty}^{+\infty} X(j(\omega-k\omega_s))\]这说明冲激采样得到的信号频谱是原信号频谱的周期性延拓。如果原信号的带宽为 $(-\omega_M, \omega_M)$2,那么要令周期延拓后信号不重叠,则必须要满足:$\omega_s>2\omega_M$(参考下图)
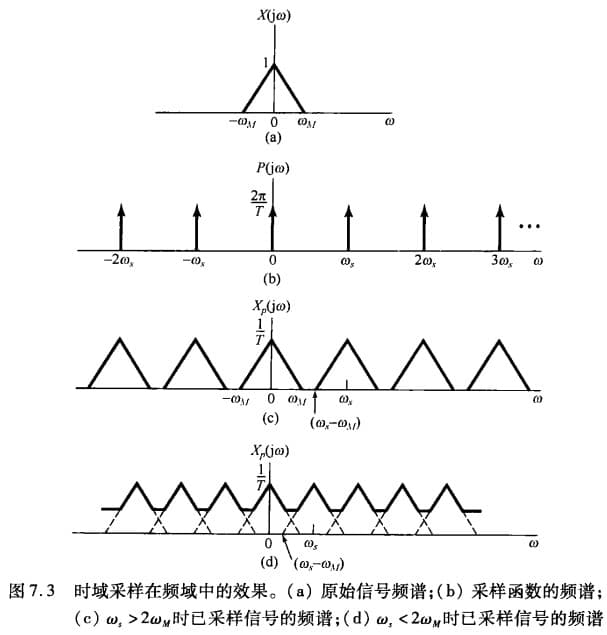
采样定理
设 $x(t)$ 是某一个带限信号,在 $\vert\omega\vert>\omega_M$ 时 $X(j\omega)=0$。如果 $\omega_s>2\omega_M$,其中,$\omega_s=2\pi/T$,那么 $x(t)$ 就唯一地由样本 $x(nT),n=0,\pm1,\pm2,\cdots$ 所确定。
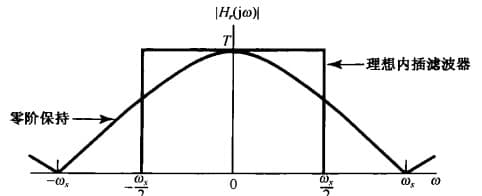
零阶保持采样
在实际中很难实现冲激信号,一般是对某一时刻的 $x(t)$ 采样并保持这一样本值,直到下一个样本被采样为止。这就称为 零阶保持(zero-order hold),相当于在冲激采样的基础上加上保持器(如下图)
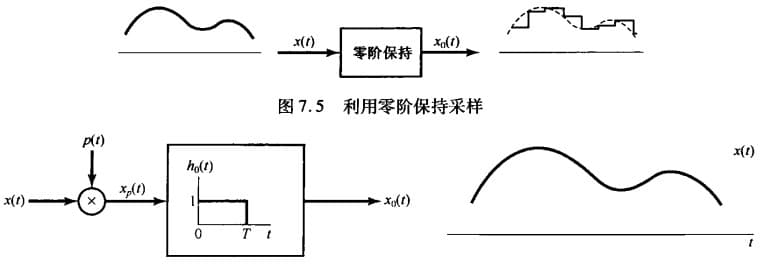
如果设保持器 $h_0(t)$ 的傅里叶变换为 $H_0(j\omega)$,则零阶保持采样频域上相当于:在冲激采样的基础上乘以 $H_0(j\omega)$,即:
\[X_p(j\omega)H_0(j\omega)\]上一节已经讲了,$X_p(j\omega)$ 可以通过低通滤波得到原频谱,即:$X(j\omega)=X_p(j\omega)H(j\omega)$,那么,我们只需找到 $H_r(j\omega)$,使得:
\[H_0(j\omega)H_r(j\omega)=H(j\omega)\\ \begin{align} \Rightarrow X_p(j\omega)H_0(j\omega)\cdot H_r(j\omega)&=X_p(j\omega)H(j\omega)\\ &=X(j\omega) \end{align}\]容易算出:
\[H_0(j\omega)=e^{-j\omega T/2} \left[ \frac{2\sin(\omega T/2)}{\omega} \right]\\ H_r(j\omega)=H(j\omega)\div \left\{ e^{-j\omega T/2} \left[ \frac{2\sin(\omega T/2)}{\omega} \right] \right\}\]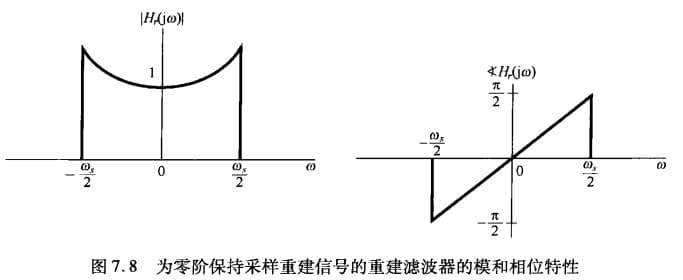
当然,由于理想低通滤波是不可能实现的,所以上图也是不可能实现的。
内插重建
上面的重建都是从频域上分析的,在时域上,重建过程就相当于在采样点之间插值,称为 内插。
对于冲激采样,其重建过程为:
\[\begin{align} x_r(t)&=x_p(t)*h(t)\\ &=\sum_{n=-\infty}^{+\infty} x(nT)h(t-nT)\\ &=\sum_{n=-\infty}^{+\infty} x(nT) \frac{\omega_c T}{\pi} \frac{\sin(\omega_c(t-nT))}{\omega_c(t-nT)} \end{align}\]可以看出,冲激采样的重建就是利用 $h(t)=\frac{\omega_c T\sin(\omega_ct)}{\pi\omega_c t}$ 作为内插函数来补充值(如下图)。这种利用理想低通滤波器的单位冲激响应的内插称为 带限内插。
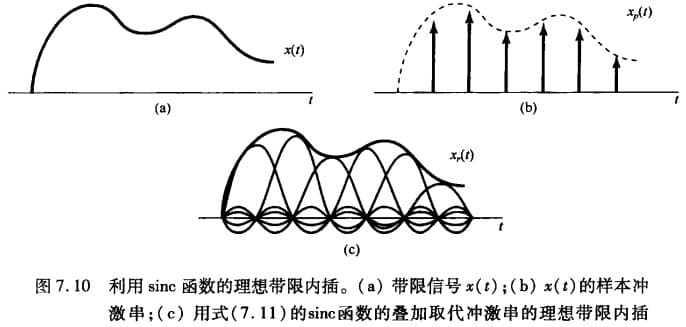
也可以利用不同的函数作为内插函数。比如把零阶保持看作内插的一种,就能得到零阶内插。(下图是零阶保持与理想内插的区别)
欠采样与混叠现象
如果 $\omega_s<2\omega_M$,周期延拓的频谱就会产生重叠,就会使得重建得到的信号失真。比如考虑:
\[x(t)=\cos\omega_0 t\]分别取 $\omega_s=6\omega_0$ 和 $\omega_s=6\omega_0/4$,则采样后的频谱图分别为:
| $\omega_s=6\omega_0$ | $\omega_s=6\omega_0/4$ | |
|---|---|---|
| 采样信号的频谱 | 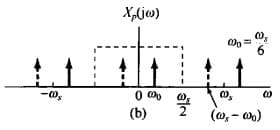 |
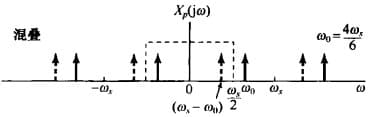 |
| 恢复的信号 | $x_r(t)=\cos\omega_0 t$ | $x_r(t)=\cos(\omega_s-\omega_0)$ |
离散时间采样
与上面的过程类似,我们有一脉冲串:
\[p(n)=\sum_{k=-\infty}^{+\infty} \delta(n-kN)\]用该脉冲串对 $x[n]$ 采样:
\[x_p[n]=x[n]p[n]=\sum_{k=-\infty}^{+\infty} x[kN]\delta(n-kN)\]其频谱为:
\[\begin{align} X_p(e^{j\omega})&=\frac{1}{2\pi}\int_{2\pi} P(e^{j\theta})X(e^{j(\omega-\theta)}) \dif \theta\\ &=\frac{1}{2\pi}\int_{2\pi} \left[ \frac{2\pi}{N} \sum_{k=-\infty}^{+\infty}\delta(\theta-k\omega_s) \right] X(e^{j(\omega-\theta)}) \dif \theta\\ &=\frac{1}{N}\sum_{k=0}^{N-1} X(e^{j(\omega-k\omega_s)}) \end{align}\]