\(\begin{align*}\newcommand{\dif}{\mathop{}\!\mathrm{d}}\end{align*}\)
信号
- 消息 message
- 人们把来自外界的报道称为消息。消息反应知识状态的改变
- 信息 information
- 消息中有意义的内容称为信息
- 信号 signal
- 信号是消息的表现形式,消息是信号的具体内容
连续时间与离散时间信号
我们用 $t$ 表示连续时间变量,$n$ 表示离散时间变量。用 $x(t)$ 表示连续时间信号,$x[n]$ 表示离散时间信号,为了区分,也称离散时间信号为离散时间序列。
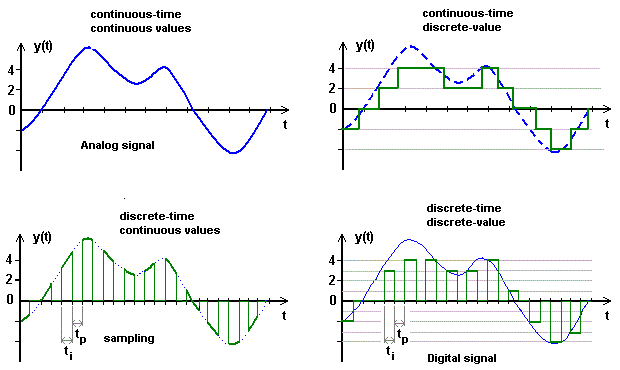
离散时间信号有两种来源,一种是自变量本身就是离散的,另一种是通过对联系时间信号进行采样的到的。
在此还要区分时间离散与幅值离散。比如模拟信号是连续时间信号;对模拟信号采样得到采样信号,是离散时间信号;对幅值进行处理就得到数字信号,是时间和幅值都离散的信号。
信号能量与功率
我们可以模仿物理上的定义来定义能量与功率:
- 能量
- 连续时间信号在 $t_1 \leq t \leq t_2$ 内的能量为:$\int_{t_1}^{t_2} |x(t)|^2 \; \rm{d} t$
- 离散时间信号在 $n_1 \leq n \leq n_2$ 内的能量为:$\sum_{n=n_1}^{n^2} |x[n]|^2$
- 若将区间扩大到 $-\infty < t \text{ or } n < +\infty$,可以得到 $E_\infty$,当然这个可能不收敛
- 功率
- 连续时间信号在 $t_1 \leq t \leq t_2$ 内的功率为:$\frac{1}{t_2 - t_1} \int_{t_1}^{t_2} |x(t)|^2 \; \rm{d} t$
- 离散时间信号在 $n_1 \leq n \leq n_2$ 内的能量为:$\frac{1}{n_2 - n_1 + 1}\sum_{n=n_1}^{n_2} |x[n]|^2$
- 若把区间扩大到 $-\infty < t < +\infty$,则有 连续时间信号:$P_\infty \triangleq \lim_{T \rightarrow \infty} \frac{1}{2T}\int_{T}^{-T} |x(t)|^2 \; \rm{d} t $,离散时间信号 $P_\infty \triangleq \frac{1}{2N+1} \sum_{n=-N}^{N} |x[n]|^2$
由于能量 $E_\infty$ = $\infty$时间 $\times$ 功率 $P_\infty$,我们可以将信号划分为以下三类(我们不研究零信号):
- 能量信号:有限能量+零功率,即 $0 \leq W_\infty<\infty, P_\infty=0$
- 功率信号:无穷能量+有限功率,即 $W_\infty \rightarrow \infty, 0\leq P_\infty <\infty$
- 其他信号:无穷能量+无穷功率,即 $W_\infty \rightarrow \infty, P_\infty \rightarrow \infty$
| 信号种 | 示例 1 | 示例 2 |
|---|---|---|
| 能量信号 |  |
 |
| 功率信号 | 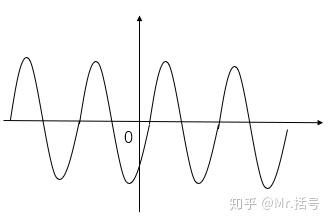 |
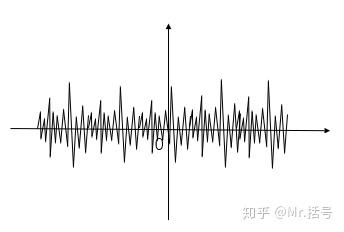 |
| 其他信号 | 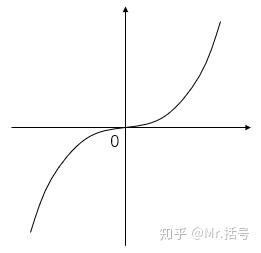 |
注意
- 直流信号和连续周期信号都是功率信号
- 功率信号与能量信号互斥,即信号不可能同时是两者
- 周期信号不一定是能量信号
自变量的变换
- 时移(time shift):$x[n]$ 延时(右移) $n_0$ 得到 $x[n-n_0]$
- 反转(time reversal):$x[n] \longrightarrow x[-n]$,$x(t) \longrightarrow x(-t)$
- 尺度变换(time scaling):
- 正常:$x(t)$;
- 2 倍速(压缩):$x(2t)$;
- 0.5 倍速(扩展):$x(t/2)$
对于连续时间信号,经过 $x(\alpha t + \beta)$ 变换后,得到的信号任然保持形状,即无损失;但对于离散时间信号,经过 $x[kn+l]$ 变换后($k, l$ 为整数),信号会损失。
注意 对周期进行运算时,注意是对 t 变换
周期信号
- 周期信号(periodic)
- 连续周期信号 $X(t+T) = x(T)$
- 离散周期信号 $x[n+N] = x[n]$
- 一个周期信号可以有多个周期 $T, 2T, 3T \cdots$,其中最小的周期称为 基波周期$T_0$(fundamental period)
注意
对于直流信号:如果是连续,则周期为 $C$($C$ 为任意实数),此时周期无意义;若为离散,则周期为 1
奇信号和偶信号
- 奇信号 even
- $x(-t)=-x(t)$ 或 $x[n]=-x[-n]$
- 偶信号 odd
- $x(-t)=x(t)$ 或 $x[n]=x[-n]$
任何信号都可以分解为一个奇信号和偶信号:
\[\begin{align} x(t) &= \frac{x(t) + x(-t)}{2} + \frac{x(t) - x(-t)}{2}\\ &= x_e(t) + x_o(t) \end{align}\]指数信号与正弦信号
- 连续时间复指数信号
- $x(t) = C e^{at}$,其中,$C, a$ 为复数
根据 $C, a$ 取值,进一步分为:
-
实指数信号:$C, a$ 都是实数
- $a>0$,单调递增
- $a<0$,单调递减
- $a=0$, 常数
-
周期性复指数信号:$a$ 为纯虚数,如 $x(t) = e^{j\omega_0 t}$
- 由欧拉公式,$x(t) = \cos\omega_0t+j\sin\omega_0t$
- 基波周期 $T_0 = \frac{2\pi}{\vert \omega_0\vert }$1,随 $\omega_0$ 增大而增大
- 我们称 $\omega$ 为 角频率 或 相频率(注意区分频率 $f_0$)
-
正弦信号 $x(t) = A \cos(\omega_0 t + \phi)$
- 基波周期 $T_0 = \frac{2\pi}{\vert \omega_0\vert }$,基波频率 $\omega_0$
-
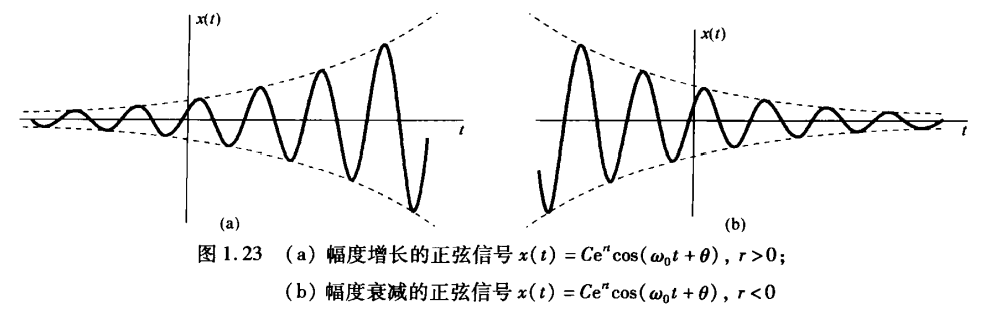
一般复指数信号: $C, a$ 为复数,设 $C = \vert C\vert e^{j \theta}$,$a = r+j\omega_0$
- $x(t) = \vert C\vert e^{j \theta} e^{rt} e^{j\omega t} = \vert C\vert e^{rt} e^{j(\omega_0 t + \theta)}$
- 振荡的峰值落在 包络线 $\pm\vert C\vert e^{rt}$ 上,当 $r<0$ 时,称为 阻尼正弦振荡(damped sinusoids)
- 离散时间复指数信号(序列)
- $x[n] = C \alpha^n$,也可表示为 $x[n] = C e^{\beta n}$,其中,$C, \alpha$ 为复数。前一种表达式更为实用。
-
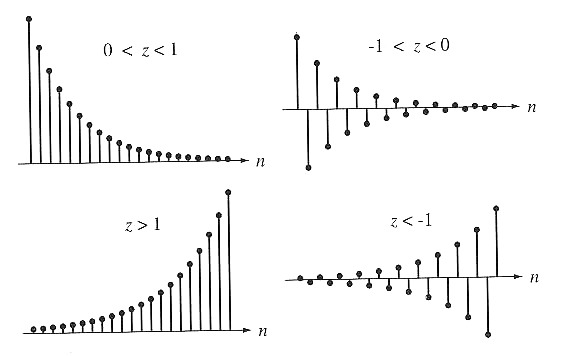
实指数信号:$C, \alpha$ 为实数
- $\vert \alpha\vert > 1$,单调递增
- $\vert \alpha\vert < 1$,单调递减
- $\alpha > 0 $,同侧
- $\alpha < 0 $,交替变换
-
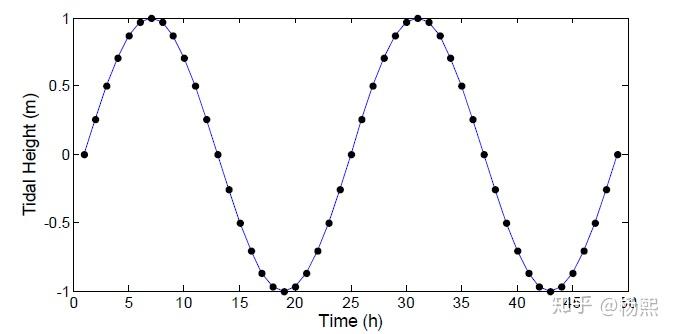
正弦信号:$\beta$ 为纯虚数,即 $\vert \alpha\vert =1$
- 由欧拉公式,$x[n] = A \cos(\omega_0 n + \phi)$
- 离散正弦信号不一定有周期,比如 在采样间隔为无理数时就无周期。(后面会进一步讨论)
-
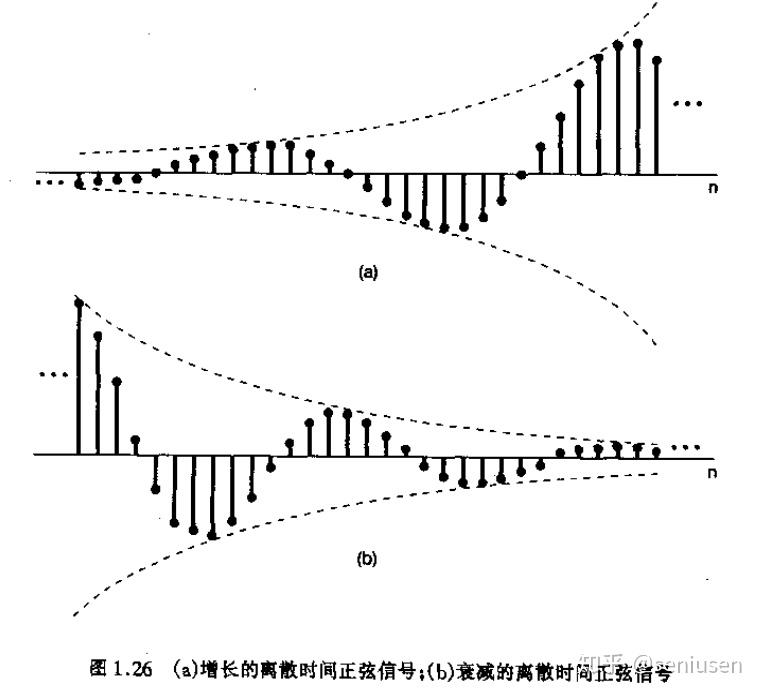
一般复指数信号:$C, \alpha$ 为复数,$C = \vert C\vert e^{j\theta}, \alpha = \vert \alpha\vert e^{j\omega_0}$
- $x[n] = \vert C\vert \vert \alpha\vert ^n \big( \cos(\omega_0n+\theta) + j \sin(\omega_0 n + \theta) \big)$
- $\vert \alpha\vert > 1$,指数增长
- $\vert \alpha\vert < 1$,指数衰减
下面我们将就 周期问题 对离散复指数信号进行分析:
对于连续复指数信号 $e^{j \omega_0 t}$,显然周期 $T_0 =2\pi/\omega_0$。但对于离散复指数信号而言,就不是这样了。因为复指数离散信号的周期 $N_0$ 必须取整数,故 $0< \omega_0 \leq 2\pi$,当 $\omega$ 取更大的值时,会有:
\[e^{j (\omega_0 + 2k\pi)n}=e^{j2\pi kn} e^{j \omega_0 n} = e^{j \omega_0 n}\]显然,上式中,$e^{j2\pi kn}$ 这一项是导致连续复指数与离散复指数这两者不同的根本原因。因此,就算增大 $\omega_0$,离散复指数也不一定频率会变大。
那么是不是 $\omega_0$ 可以取 $(0, 2\pi]$ 内任何值呢?要满足周期函数定义 $e^{j \omega_0 (n+N)} = e^{j \omega_0 n}$,则必须有:$e^{j \omega_0 N} = 1$,即:
\[\begin{align} \omega_0 N &= 2\pi m ,\; m \in \mathbb{N}\\ \text{即:} \frac{\omega_0}{2 \pi} &= \frac{m}{N} \end{align}\]$m,N$ 都是整数,也就是说,若 $\omega/2\pi$ 为有理数,$\omega$ 是 $\pi$ 的有理数倍时,则 $e^{j\omega_0 n}$ 是周期性的;否则就不是周期性,比如 $x[n]=\cos(n/6)$。
在 $(0, 2\pi]$ 中有两个特殊的值,$\pi$ 和 $2\pi$,当 $\omega_0 = \pi$ 时,$x[n]$剧烈变化,每个 n 都会改变符号;而当 $\omega_0 = 2\pi$ 时,$x[n]$ 始终为 1. 我们把 $\omega$ 在 $\pi$ 附近的作为高频,在 $0$ 和 $2\pi$ 附近的为低频。
单位冲激与单位阶跃
离散时间信号
单位脉冲(unit impulse) 或 单位样本(unit sample) 或 脉冲
\[\delta[n] = \begin{cases} 0, \; n \neq 0\\ 1, \; n = 0 \end{cases}\]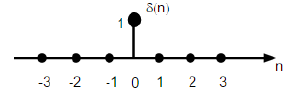
可以用于提取信号 $x[n]$ 中某一点的样本。比如,信号 在 $n=0$ 处的采样为 $x[n]\delta[n] = x[0]\delta[n]$;信号 在 $n = n_0$ 处的采样为 $x[n]\delta[n-n_0] = x[n_0]\delta[n-n_0]$. 于是,我们可以发现任何序列都可以用一组幅度加权的延迟单位样本序列的和来表示:
\[x[n] = \sum_{k=-\infty}^\infty x[k] \delta[n-k]\]单位阶跃序列(unit step)
\(u[n] = \begin{cases} 0, \; n < 0\\ 1, \; n \geq 0 \end{cases}\)
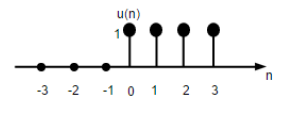
显然,离散时间单位脉冲 是 离散时间单位阶跃 的 一次差分(first difference),即 $\delta[n] = u[n] - u[n-1]$
而离散时间单位阶跃 是 离散时间单位脉冲 的 求和函数(runnning sum),即 $u[n] = \sum_{m=-\infty}^{n} \delta[m]$,此外,序列 $u[n]$ 也可表示成一组延迟的单位样本序列之和:
\[u[n] = \delta[n] + \delta[n-1] + \delta[n-2] + \cdots = \sum_{k=0}^\infty \delta[n-k]\]连续时间信号
单位阶跃
\(u(x) = \begin{cases} 0, \; n < 0\\ 1, \; n \geq 0 \end{cases}\\ \text{或:} u(x) = \lim_{\Delta \rightarrow 0}u_\Delta(x)\)

单位阶跃可以用于模拟开关、起始一个函数和截取信号。比如要截取 $t \sim t_0$的信号,则可以用:
\[f(t) = u(x) - u(x-x_0)\]单位冲击
\[\begin{cases} \int_{-\infty}^\infty \delta(t) = 1 \rightarrow \text{强度为1} \\ \delta(t) = \begin{cases} 0, \; t \ne 0\\ \infty, \; t=0 \end{cases} \end{cases}\\ \text{或:}\delta(t) = \lim_{\Delta \rightarrow 0} \delta_\Delta(t)\]
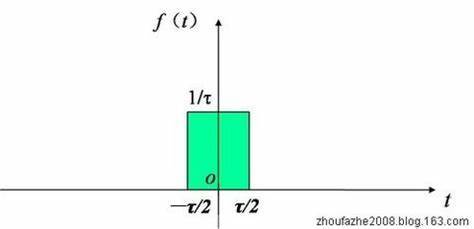
单位冲击可以用于取样某个函数:
\[\int_{-\infty}^\infty f(t) \delta(t-t_0) \dif t = f(t_0)\]导数性质: \(\begin{align} f(t)\delta'(t) &= [f(t)\delta(t)]'-f'(t)\delta(t)\\ &= f(0)\delta'(t) - f'(0)\delta(t) \end{align}\)
尺度变换性质:
\[\delta^{(n)} (at) = \frac{1}{|a|} \cdot \frac{1}{a^n} \delta^{(n)}(t)\]推论:
- $\delta(at) = \frac{1}{\vert a\vert } \delta(t)$
- $\delta(at - t_0) = \frac{1}{\vert a\vert } \delta(t - \frac{t_0}{a})$
- 当 $a=-1$ 时,$\delta^{(n)}(-t) = (-1)^n \delta^{(n)}(t)$
- $\delta(t) = \delta(-t)$
- $\delta’(t) = -\delta’(-t)$
本节考点
- 信号自变量的变换
- 信号的奇偶分解
-
连续复指数信号的周期:$e^{j \omega_0 t} = e^{j \omega_0 (t+T)} = e^{j \omega_0 t} e^{j \omega T}$,显然,要使 $x(t)$ 有周期性,则 $e^{j \omega_0 T} = 1$,推导出 $T_0 = \frac{2\pi}{\vert \omega_0\vert }$ ↩