置信区间
定义
设总体 $X$ 的分布函数 $F(x;\theta)$,$\theta$ 未知,对给定值 $\alpha(0<\alpha<1)$,有两个统计量:
\[\hat{\theta}_L=\hat{\theta}_L(X_1,\cdots,X_n)\\ \hat{\theta}_U=\hat{\theta}_U(X_1,\cdots,X_n)\]使得:
\[P\{ \hat{\theta}_L \leq \theta \leq \hat{\theta}_U \} \geq 1-\alpha\]$(\hat{\theta}_L, \hat{\theta}_U)$ 称为 $\theta$ 的 置信水平 为 $1-\alpha$ 的 双侧置信区间;$\hat{\theta}_L$ 称为 双侧置信下限,$\hat{\theta}_U$ 称为 双侧置信上限。
这里有两种理解方式,一种是 $\theta$ 落在 $(\hat{\theta}_L, \hat{\theta}_U)$ 内的可能是 $1-\alpha$,另一种是,反复抽样多次,确定多个 $(\hat{\theta}_L, \hat{\theta}_U)$,则包含 $\theta$ 的占 $1-\alpha$
定义
如果 $P{ \hat{\theta}_L < \theta }\geq 1-\alpha$,则 $\hat{\theta}_L$ 称为 $\theta$ 的置信水平为 $1-\alpha$ 的单侧置信下限。
如果 $P{ \hat{\theta}_U > \theta }\geq 1-\alpha$,则 $\hat{\theta}_U$ 称为 $\theta$ 的置信水平为 $1-\alpha$ 的单侧置信上限。
单侧置信下限、上限与双侧置信区间的关系:
\[P\{ \hat{\theta}_L < \theta \}\geq 1-\alpha_1\\ P\{ \hat{\theta}_U > \theta \}\geq 1-\alpha_2\\ P\{ \hat{\theta}_L \leq \theta \leq \hat{\theta}_U \} \geq 1-\alpha_1-\alpha_2\]定义
称置信区间 $(\hat{\theta}_L, \hat{\theta}_U)$ 的平均长度 $E(\hat{\theta}_U-\hat{\theta}_L)$ 为区间的精确度,精确度的一半为误差限
置信水平高,精确度低。所以这两者是相互制约的。但同一置信水平可能对应多个精确度,这种情况下,我们遵循 Neyman原则:在置信水平达到 $1-\alpha$ 的置信区间中,选精确度尽可能高的置信区间。
置信区间的选取
求置信区间的方法:
- 找到一个与参数和样本有关的随机变量 $G$,使 $G$ 分布已知
- 找 $a,b\;(a<b)$,使 $P(a<G<b)\geq 1-\alpha$
- 要求 $\theta$ 的区间估计,则 $G$ 应该是 $\theta$ 和样本的函数。故可以从 $a<G<b$ 解出 $\hat{\theta}_L < \theta <\hat{\theta}_U$
这里我们称 $G=G(X_1,\cdots,X_n;\theta)$ 称为 枢轴量
枢轴量与统计量的区别:
- 枢轴量是样本与(一个)待估参数的函数,其分布不依赖未知参数
- 统计量是样本的函数,其分布依赖于未知参数
如果有多个 $a,b$ 满足 $P(a<G<b)\geq 1-\alpha$,则优先选择满足 Neyman 原则的;如果最优解不存在或比较难求,则取 $P(G\leq a)=P(G\geq b)=\alpha/2$,对应的 $\hat{\theta}_L$、$\hat{\theta}_U$ 的置信度为 $1-\alpha/2$
一般 $G$ 是矩估计或极大似然估计。常见的枢轴量如下:
-
单个正态总体 $N(\mu,\sigma^2)$
\[\begin{cases} \mu 的枢轴量 \begin{cases} \dfrac{\bar{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) & \sigma^2 已知\\ \dfrac{\bar{X}-\mu}{S/\sqrt{n}}\sim t(n-1) & \sigma^2 未知 \end{cases} \\ \sigma^2 的枢轴量 \begin{cases} \dfrac{\sum_{i=1}^n(X_i - \mu)^2}{\sigma^2}\sim\chi^2(n) \quad \mu已知\\ \dfrac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1) \quad \mu未知 \end{cases} \end{cases}\] -
两个正态总体 (学的时候没认真听,以后补上)
\[\]
单个正态总体的区间估计
$\sigma^2$ 已知,求 $\mu$
取枢轴量 $G=\dfrac{\bar{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)$,则 $P{ a< G < b } \leq 1-\alpha$ 等价于:
\[P\{ \overline{X}-\frac{\sigma}{\sqrt{n}} b < \mu < \overline{X} - \frac{\sigma}{\sqrt{n}}a \} \geq 1-\alpha\]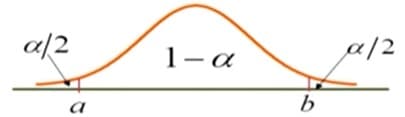
由标准正态分布的对称性可知,$a=-b=-z_{\alpha/2}$,$z_{\alpha/2}$ 是正态分布的上 $\alpha/2$ 分位数(可查表得到),此时的区间长度 $L=2z_{\alpha/2}/\sqrt{n}$ 最短。
$\sigma^2$ 未知,求 $\mu$
用样本方差 $S^2$ 估计 $\sigma^2$,得到枢轴量 $G=\dfrac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1)$,从而
\[P\{ \overline{X}-\frac{S}{\sqrt{n}} b < \mu < \overline{X} - \frac{S}{\sqrt{n}}a \} \geq 1-\alpha\\ a=-b=-t_{\alpha/2}(n-1)\]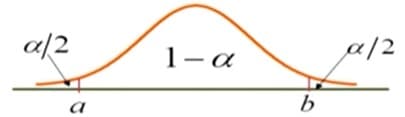
$t$ 分布与正态分布的图像类似。
$\mu$ 已知,求 $\sigma^2$
取枢轴量为 $G=\dfrac{\sum_{i=1}^n(X_i - \mu)^2}{\sigma^2}\sim\chi^2(n)$,则:
\[\chi^2_{1-\alpha/2}(n) < \frac{\sum_{i=1}^n(X_i - \mu)^2}{\sigma^2} < \chi^2_{\alpha/2}(n)\\ \frac{\sum_{i=1}^n(X_i - \mu)^2}{\chi^2_{\alpha/2}(n)} < \sigma^2 < \frac{\sum_{i=1}^n(X_i - \mu)^2}{\chi^2_{1-\alpha/2}(n)}\]$\mu$ 未知,求 $\sigma^2$
由 $\sigma^2$ 的估计 $S^2$ ,取枢轴量 $G=\dfrac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)$,则:
\[\chi^2_{1-\alpha/2}(n-1) < \frac{(n-1)S^2}{\sigma^2} < \chi^2_{\alpha/2}(n-1)\\ \frac{(n-1)S^2}{\chi^2_{\alpha/2}(n-1)} < \sigma^2 < \frac{(n-1)S^2}{\chi^2_{1-\alpha/2}(n-1)}\]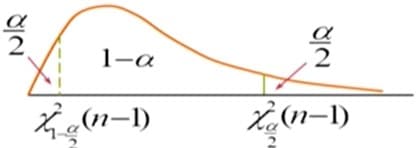
总结
