\(\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\p}{\partial} \end{align*}\)

连续随机变量与概率密度

定义 对于随机变量 $X$ 的分布函数，若存在非负函数 $f(x)$，使得对于任意实数 $x$ 有：

\[F(x)=P\{X\leq x\}\\ F(x)=\int_\infty^x f(t) \dif t\\ \Leftrightarrow f(x)= \begin{cases} F'(x) & 可导\\ 0 & 不可导 \end{cases}\]

则称 $X$ 为 连续型随机变量，其中 $f(x)$ 称为 $X$ 的 概率密度函数，简称 概率密度。

注意 性质：

1. $f(x)\geq 0$
2. $\int_{-\infty}^{\infty} f(x)\dif x=1$
3. $P(x_1<X<x_2)=\int_{x_1}^{x_2} f(t)\dif t$
4. 在 $f(x)$ 连续点，$F’(x)=f(x)$，也就是落在 $(x, x+\dif x)$ 内的概率为 $f(x)\dif x$
5. 另外，$F(x)$ 一定连续

$f_1(x), f_2(x)$ 是两个概率密度，问 $f_1(x)\cdot f_2(x)$，$f_1(x)+f_2(x)$ 是否是概率密度？

$f_1(x)\cdot f_2(x)$ 和 $f_1(x)+f_2(x)$ 都不是，因为不满足第2条性质。

均匀分布

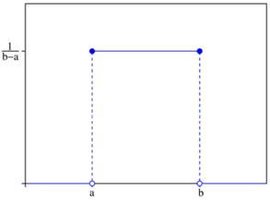
定义 若 $X$ 的概率密度函数为：

\[f(x)= \begin{cases} \frac{1}{b-a} & x\in(a,b)\\ 0 & x\notin(a,b) \end{cases}\\ F(x)= \begin{cases} 0 & x<a\\ \frac{x-a}{b-a} & a\leq x<b\\ 1 & x\geq a \end{cases}\]

则称 $X$ 服从 $(a,b)$ 上的均匀分布（Uniform），记为 $X\sim \text{U}(a,b)$ 或 $X\sim \text{Unif}(a,b)$

指数分布

定义 若 $X$ 的概率密度函数为：

\[f(x)= \begin{cases} \lambda e^{-\lambda x} & x>0\\ 0 & x\leq 0 \end{cases}\\ 其中，\lambda >0\]

则称 $X$ 服从 指数分布，记为 $X \sim E(\lambda)$。其分布函数为：

\[\begin{align} F(x)&=\int_{-\infty}^{x} f(x) \dif x\\ &= \begin{cases} 1-e^{-\lambda x} \dif x & x\geq 0\\ 0 & x<0 \end{cases} \end{align}\]

正态分布

定义 若 $X$ 的概率分布函数为：

\[f(x)=\frac{1}{\sqrt{2\pi}\sigma} e^{- \frac{(x-\mu)^2}{2\sigma^2}},\;-\infty<x<+\infty\\ 其中，\mu为常数，\sigma>0\]

则称 $X$ 服从参数为 $\mu,\sigma$ 的 正态分布（高斯分布） 记为 $X\sim\text{N}(\mu, \sigma^2)$

特征

1. $f(x)$ 关于 $x=\mu$ 对称
2. $x\leq\mu$ 时，是严格单调递增函数
3. $f_\max=f(\mu)=\frac{1}{\sqrt{2\pi}\sigma}$
4. $\lim_{\vert x-\mu \vert\rightarrow\infty} f(x)=0$
5. 改变 $\mu$，图像的形状不变，中心平移，$\mu$称为 位置参数
6. 改变 $\sigma$，图像的中心不变，形状改变，且 $\mu$ 越大，图像越胖。$\sigma$ 称为 尺度参数（决定曲线的分散程度）

正态分布的概率计算

若 $X\sim\text{N}(\mu, \sigma^2)$，对实数 $x$：

\[P(X\leq x)=\frac{1}{\sqrt{2\pi} \sigma} \int_{-\infty}^x e^{- \frac{(t-\mu)^2}{2\sigma^2}} \dif t\]

然而这个积分极难求出原函数，完全算不出来。所幸，我们可以借助标准正态分布来计算。

定义 若 $Z\sim\text{N}(0,1)$，称 $Z$ 服从标准正态分布，其概率密度函数为：$\varphi(z)=\frac{1}{\sqrt{2\pi}} e^{-z^2/2}$，分布函数为 $\Phi(z)=\int_{-\infty}^z \frac{1}{\sqrt{2\pi}} e^{-t^2/2} \dif t$。以后 $\varphi(z)$，$\Phi(z)$ 默认表示标准正态分布。

标准正态分布的概率分布函数已经计算出来了，我们能查表得到特定值的概率。（注意：$\Phi(-z)=1-\Phi(z)$ ）

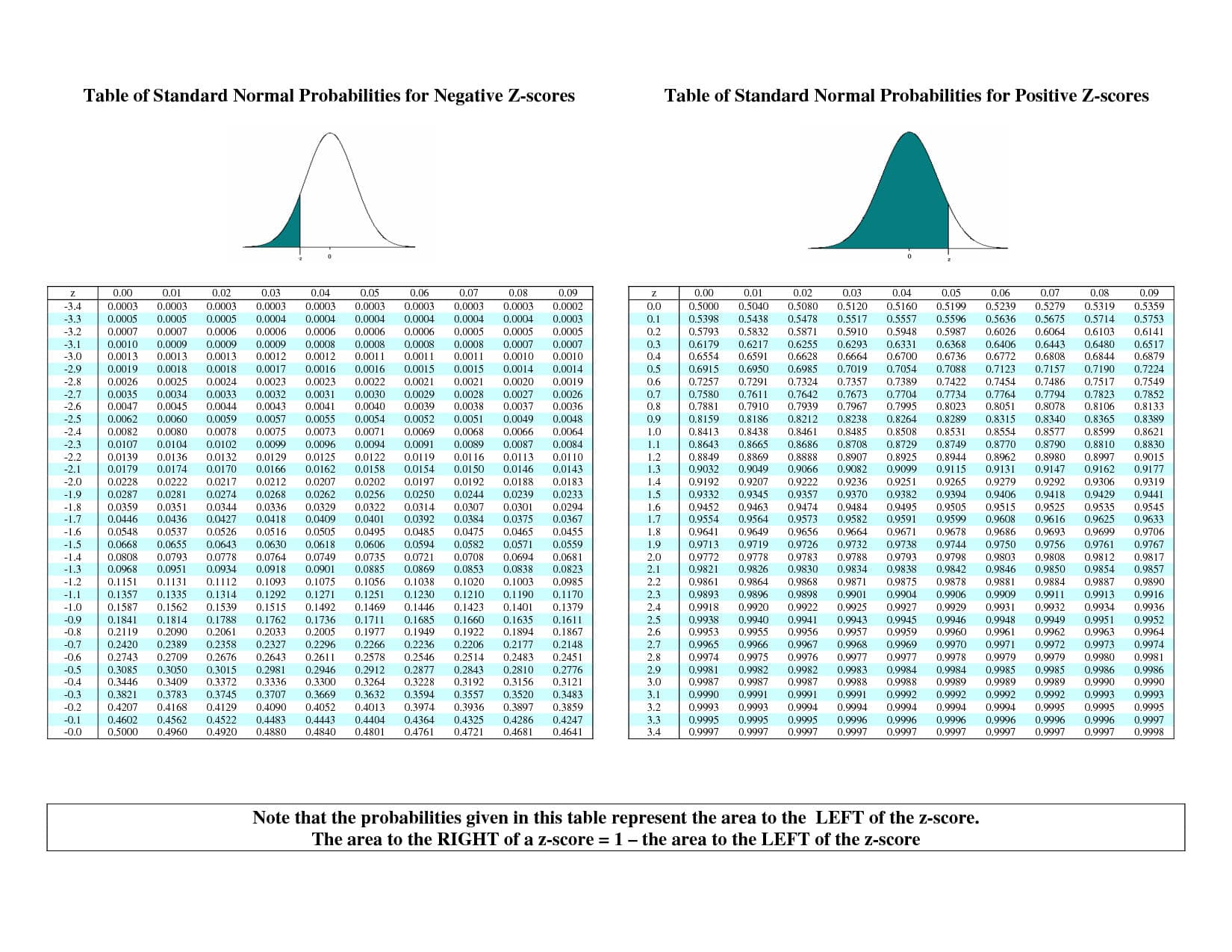
那么如何计算一般的正态分布呢？我们有如下性质：

性质 当 $X\sim\text{N}(\mu,\sigma^2)$ 时，$\frac{X-\mu}{\sigma}\sim\text{N}(0,1)$

证明 对于任意实数 $z$

\[P(\frac{X-\mu}{\sigma}\leq z)=P(X\leq \sigma z+\mu)= \int_{-\infty}^{\sigma z+\mu} \frac{1}{\sqrt{2\pi} \sigma} e^{- \frac{(t-\mu)^2}{2\sigma^2}} \dif t\\ 令 s=\frac{t-\mu}{\sigma} \Longrightarrow \int_{-\infty}^{z} \frac{1}{\sqrt{2\pi}} e^{-\frac{s^2}{2}} \dif s=\Phi(z)\]

由这条性质可知，当 $X\sim\text{N}(\mu,\sigma^2)$ 时，要计算 $P(X\leq a)$，可以转化为：$(X\leq a)=P(\frac{X-\mu}{\sigma}\leq\frac{a-\mu}{\sigma})=\Phi(\frac{a-\mu}{\sigma})$

例题：$X\sim N(\mu,\sigma^2)$，$y^2+4y+X=0$ 无实根的概率是 1/2，问 $\mu = ?$

解：无实根即 $\Delta = 16-4X<0$，即 $X>4$，$P(X>4)=1/2$，$\therefore \mu = 4$

---

以上列出的分布要熟记。