\(\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\p}{\partial} \end{align*}\)
分布函数
联合分布函数
设 $(X,Y)$ 是二元随机变量,二元函数:
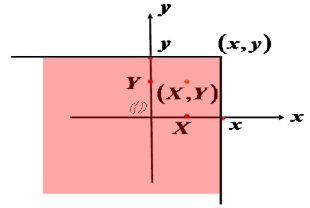
\[F(x,y)=P\{ (X\leq x)\cup(Y\leq y) \} = P(X\leq x, Y\leq y)\]称为二元随机变量 $(X, Y)$ 的 联合分布函数。(同样适用于离散型)
性质
- $0\leq F(x,y) \leq 1$
- $F(x,y)$ 关于 $x,y$ 单调增
- $F(x,y)$ 关于 $x,y$ 右连续
-
- $F(+\infty, +\infty)=1$
- $F(-\infty, y)=F(x, -\infty)=F(-\infty, -\infty)=0$
- $F(-\infty, +\infty)=F(+\infty, -\infty)=0$
-
若 $x_1<x_2$,$y_1<y_2$,则有
\[P(x_1<X\leq x_2, y_1<Y\leq y_2)\\ =F(x_2,y_2)-F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1)\geq 0\]
边际分布函数
$F_X(x)=F(x,+\infty)=P(X\leq x)$,$F_Y(y)=F(+\infty, y)=P(Y\leq y)$ 称为 $X,Y$ 的边际分布函数
条件分布函数
若 $P(Y=y)>0$,则在 $Y=y$ 条件下,$X$ 的条件分布函数为:
\[F_{X|Y}(x|y)=P(X\leq x| Y=y)=\frac{P(X\leq x, Y=y)}{P(Y=y)}\]但对于连续型随机变量,$F(Y=y)=0$,所以我们换另一种定义:
\[F_{X|Y}(x|y)=\lim_{\varepsilon\rightarrow 0^-} P(X\leq x| y<Y\leq y+\varepsilon )\\ =\lim_{\varepsilon\rightarrow 0^-} \frac{P(X\leq x, Y=y)}{P(y<Y\leq y+\varepsilon)}\]联合概率密度
对于二元随机变量 $(X,Y)$ 的分布函数 $F(x,y)$,如果存在非负可积函数 $f(x,y)$,有:
\[F(x,y)=\int_{-\infty}^x\int_{-\infty}^y f(u,v) \dif u \dif v\\ f(x,y)= \begin{cases} \dfrac{\p^2 F}{\p x\p y} & F 二阶可偏导\\ 0 & 其他 \end{cases}\]则称 $(X,Y)$ 为二元连续型随机变量,并称 $f(x,y)$ 为联合概率密度函数
性质:
- $f(x,y)>0$
- $\int_{-\infty}^{+\infty}\int_{y=-\infty}^{+\infty} f(u,v) \dif u \dif v =1$
- $P((X,Y)\in D)=\iint_D f(x,y)\dif x\dif y$
边际概率密度
若联合概率密度为 $f(x,y)$,则边际概率密度:
\[f_X(x)=\int_{-\infty}^{+\infty} f(x,y)\dif y\\ f_Y(y)=\int_{-\infty}^{+\infty} f(x,y)\dif x\]根据 $F_X(x)$ 的定义有:
\[F_X(x)=F(x,+\infty)=P(X\leq x, Y<+\infty)\\ =\int_{-\infty}^x \left[ \int_{-\infty}^{+\infty} f(u,y)\dif y \right] \dif u=\int_{-\infty}^x f_X(u)\dif u\]条件概率密度
对于固定的 $y$,$f_Y(y)>0$,且 $f_Y(y)$ 连续,则在 $Y=y$ 的条件下,$X$ 的条件概率密度为:
\[f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}\]常见的二元分布
均匀分布
$D$ 为有界区域,$(X,Y)$ 的联合分布为:
\[f(x,y)= \begin{cases} 1/A & (x,y)\in D\\ 0 & (x,y)\notin D \end{cases}\\ A 是 D 的面积\]记为:$(X,Y) \sim U(D)$
正态分布
\[f_{X,Y}(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho}}\cdot\\ \exp\left\{ -\frac{1}{2(1-\rho^2)}\left( \frac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2} \right) \right\}\]记为 $(X,Y) \sim N(\mu_1,\mu_2;\sigma_1^2,\sigma_2^2;\rho)$
我们不需要记那一大串公式,但要把上一行的写法记住。
注:二元正态分布的边缘分布是正态分布,但是,两个一元分布的组合不一定是二元正态分布。
独立
定义 若满足 $F(x,y)=F_X(x)\cdot F_Y(y)$ ,则称 $(X,Y)$ 独立。
但是这种方法并不好判断。我们常用如下等价条件:
定价条件
- 离散型:$X,Y$ 独立 $\Leftrightarrow$ $p_{ij} = p_{i\cdot} \times p_{\cdot j}$
- 连续型:$X,Y$ 独立 $\Leftrightarrow$ $f(x,y)=f_X(x)f_Y(y)$
Z=X+Y 的分布
设 $(X,Y)$ 的概率密度为 $f(x,y)$,则 $Z=X+Y$ 的分布函数为:
\[F_Z(z)=P(Z\leq z)=\iint_{x+y\leq z} f(x,y)\dif x \dif y\\ =\int_{-\infty}^{+\infty} \left[ \int_{-\infty}^{z-y} f(x,y)\dif x \right] \dif y\\ =\int_{-\infty}^{+\infty} \left[ \int_{-\infty}^{z} f(u-y,y)\dif u \right] \dif y\\ =\int_{-\infty}^{z} \left[ \int_{-\infty}^{+\infty} f(u-y,y)\dif y \right] \dif u\\ =\int_{-\infty}^z f_Z(u) \dif u\]而概率密度 $f_Z(z)$ 为:
\[f_Z(z)=\int_{-\infty}^{+\infty} f(z-y, y) \dif y\\ 或 =\int_{-\infty}^{+\infty} f(x, z-x) \dif x\]当 $X$ 和 $Y$ 相互独立时,$Z$ 的概率密度公式称为卷积公式:
\[f_Z(z)=\int_{-\infty}^{+\infty}f_X(z-y)f_Y(y)\dif y=\int_{-\infty}^{+\infty} f_X(x) f_Y(z-x)\dif x\]特殊的,独立的两个正态分布相加还是正态分布,并满足:
- $\xi_1\sim \rm{N}(\mu_1, \sigma_1^2)$,$\xi_2\sim \rm{N}(\mu_2, \sigma_2^2)$,$\xi_1,\xi_2$ 独立,$\eta=\xi_1+\xi_2$,则:$\eta\sim \rm{N}(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2)$
- $\xi_1\sim \rm{N}(\mu_1, \sigma_1^2)$,$\xi_2\sim \rm{N}(\mu_2, \sigma_2^2)$,$\xi_1,\xi_2$ 独立,$\eta=a\xi_1+b\xi_2$,则:$\eta\sim \rm{N}(a\mu_1+b\mu_2, a^2\sigma_1^2+b^2\sigma_2^2)$
Z=X/Y 的分布
若 (X,Y) 的概率密度为:$p(x,y)$,则:
(待证)