什么是假设检验:假如你是法官,则根据“疑罪从无”,我们先假设被告人无罪;如果有证据推翻了这一假设,则说明被告有罪。
假设检验的过程:
- 建立两个完全对立的假设:原假设(零假设) $H_0$,备择假设(对立假设) $H_1$
- 原假设与备择假设是不对称的,一般根据立场、惯例、方便性来选择。一般有如下几个原则:
- 保护原假设:如果假设 $A$ 误判为假的后果更严重,则 $A$ 作为原假设。比如:“某种药物有毒副作用” 应该为原假设
- 原假设为维持现状:原假设常选取“无效果”、“无改进”、“无差异”,从而拒绝原假设表示有较强的理由支持备择假设。比如:“某种药物没有减肥效果”应为原假设
- 原假设取简单假设:只有一个参数的假设称为简单假设。如果只有一个假设是简单假设,则将其作为原假设。比如:
- 左边检验:$H_0:\theta=\theta_0$,$H_1=\theta<\theta_0$(效果与 $H_0:\theta\geq\theta_0$,$H_1=\theta<\theta_0$ 相同)
- 右边检验:$H_0:\theta=\theta_0$,$H_1=\theta>\theta_0$ (效果与 $H_0:\theta\leq\theta_0$,$H_1=\theta>\theta_0$ 相同)
- 双边检验:$H_0:\theta=\theta_0$,$H_1=\theta\neq\theta_0$
- 检验假设:根据收集到的数据,通过临界值法、P值法等方法进行判断
- 与原假设 $H_0$ 相关的统计量 $T=T(X_1,\cdots,X_n)$ 称为 检验统计量,相应的,拒绝原假设的样本值的范围称为 拒绝域 $W$,补集 $\overline{w}$ 称为 接受域
由于样本具有随机性,所以在检验时可能会出现如下两类错误:
| 原假设为真 | 原假设为假 | |
|---|---|---|
| 拒绝原假设 | 第Ⅰ类错误(弃真) | 正确 |
| 接受原假设 | 正确 | 第Ⅱ类错误(取伪) |
对应犯错的概率:
\[\alpha=P(Ⅰ类错误)\\ \beta=P(Ⅱ类错误)\]
设总体满足某正态分布 $X\sim N(\mu,1)$,样本均值满足 $\overline{X}\sim N(\mu,\frac{1}{n})$。
$H_0:\mu=\mu_0$,$H_1:\mu=\mu_1(>\mu_0)$,拒绝域:$\overline{X}\geq C$,求 $\alpha,\beta$。
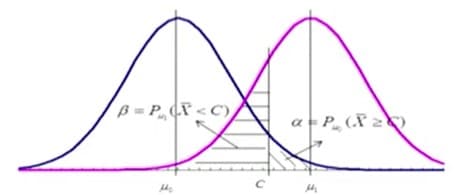
解:$C$ 的右边是拒绝域,拒绝域与 $P_{\mu_0}$ 的交集即第一类错误;同理,接受域与 $P_{\mu_1}$ 的交集即第二类错误。故:
$$
\alpha = P_{\mu_0}(\overline{X}\geq C)\\
\beta = P_{\mu_1}(\overline{X}<C)
$$
从上题中可以看出,两类错误是相互制约的,$\alpha$ 小,$\beta$ 就会增大。为了找到一个平衡点,我们引入 Neyman-Pearson 原则:
- 首先控制第一类错误的概率不超过某个常数 $\alpha\in(0,1)$(称为 显著水平),再寻找检验 $C$,使犯第二类错误的概率尽可能小。
常取 $\alpha=0.01,0.05,0.1$ 等。
这里我们就可以介绍 临界值法:先取一定的显著水平,然后根据原假设的统计量的分布确定临界值,最后将样本与临界值进行比较,得出结论。
例题:某种减肥药宣称有减肥效果。9 位试验者服用后,减肥前的体重减去减肥后的体重如下:1.5, 0.6, -0.3, 1.1, -0.8, 0, 2.2, -1.0, 1.4。问该减肥药是否有减肥效果?
解:可以认为体重服从正态分布。原假设 $H_0$:无减肥效果,$\mu=0$;备择假设 $H_1$:有减肥效果 $\mu>0$。
若原假设成立,则 $\frac{\overline{X}}{0.6/\sqrt{9}}\sim N(0,1)$,犯第一类错误的概率如下:
$$
\begin{align}
P\{\overline{X}\geq C | \mu=0 \}&=P\{\frac{\overline{X}}{\sigma/\sqrt{n}}\geq \frac{C}{\sigma/\sqrt{n}} \Big| \mu=0 \}\\
&=1-\Phi(\frac{C}{\sigma/\sqrt{n}})\leq \alpha=0.05
\end{align}\\
$$
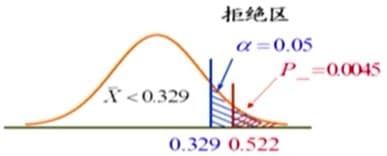
通过查表可知,正态分布的上0.05分位数为:1.645,故:$\frac{C}{0.6/\sqrt{9}}\geq 1.645 $$\Rightarrow C \geq 0.329\\$。为了使犯第Ⅱ类错误的概率尽可能小,取 $C=0.329$。拒绝域为 $W=\{\overline{X}\geq0.329\}$。
而样本均值为 $0.522>0.329$,当原假设成立时,样本落在拒绝域的概率不超过 0.05,是小概率事件,根据实际推断原理,有充分理由拒绝原假设。故该减肥药有减肥效果。
我们也可以反过来,将观察结果设为临界水平,然后计算此时的犯第一类错误的概率 $P_-$,如果 $P_-$ 比 $\alpha$ 小,说明样本落入了拒绝区,就拒绝原假设。这种方法称为 $P_-$ 值法
(还是上面的例题)解:
$$
\begin{align}
P_-&=P\{ \overline{X} \geq 0.522 | \mu=0 \}\\
&=1-\Phi(\frac{0.522}{0.6/\sqrt{9}})=0.0045<\alpha=0.05
\end{align}\\
故拒绝原假设
$$
大但假设,小心检验。