随机变量
前面我们的事件分为两类:数值的和非数值的(数值:扔骰子;非数值:是否射中)。对于非数值的,我们为了方便研究,也把它看作数值的,所以我们定义随机变量。
定义
- 随机变量
- 定义在样本空间 $\Omega$ 上的实函数 $X=X(\omega), \omega\in\Omega$。$X$ 称为随机变量,一般简记为 $X$,是一个从样本空间到实数的映射。
-
随机事件可以用随机变量表示为 $A={e:X(e)\in I}={X\in I}$ $I\in\mathbb{R}$,即随机事件对应于某个范围的随机变量
注释
- 对于 $i\neq j$,必有 ${X=i}\cap{X=j}=\varnothing$
- 允许出现多个事件对应一个随机变量
- 一般用大写字母 $X、Y、Z$ 或希腊字母 $\xi, \eta$ 来表示随机变量
分布函数
- 分布函数
-
设 $X$ 是一个随机变量,$x$ 是任意实数,函数 $F(x)=P{\omega X(\omega)\leq x}$ 称为随机变量 $x$ 的分布函数,记作 $F_X(x)$ 或 $F(x)$,有时也简记为 $F_X(x)=P{X\leq x}$。 - 该定义适用于连续随机变量和离散随机变量。
分布函数给出了随机变量落入任意一个范围的可能性。
对于 $\forall a<b$,可以用分布函数表达如下概率:
- $P(X<a)=F(a-0)$
- $P(X=a)=F(a)-F(a-0)$
- $P(a<X\leq b)==P(X \leq b) - P(X \leq a)=F(b)-F(a)$
- $P(a\leq X \leq b)=P(X\leq b) - P(X< a)=F(b)-F(a-0)$
盒中有编号分别为1,2,2,3,3,3的球,随机摸一个球,用 $X$ 表示摸到球的球号。求 $X$ 的分布函数。
显然,$P(X=1)=1/6$,$P(X=2)=1/3$,$P(X=3)=1/2$,故分布函数为:
$$
F(X)=P(X\leq x)=
\begin{cases}
0, x<1\\
1/6, 1\leq x<2\\
1/2, 2\leq x<3\\
1, x\geq3
\end{cases}
$$
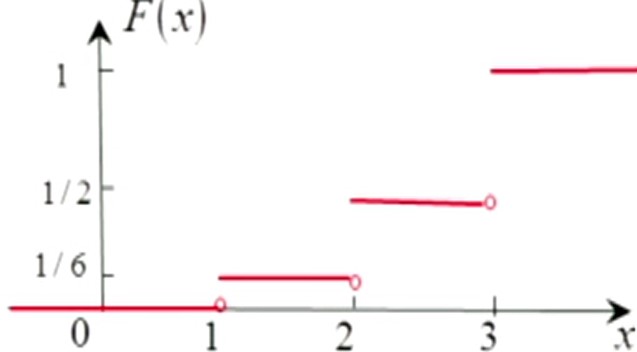
利用上图解释一下 $F(x-0)$ 和 $F(x+0)$ 的不同。对于连续点,$F(x-0)=F(x+0)$;对于非连续点,比如上图中,$x=1$,则 $F(1-0)=0\neq F(1)$,$P(1+0)=1/6 = F(1)$ (右连续)
分布函数的性质:
-
$F(x)$ 是单调增函数
\[\because \forall x_1<x_2, 有 0\leq P(x_1<X\leq x_2)=F(x_2)-F(x_1)\\ \therefore F(x_1)<F(x_2)\] - $0\leq F(X)\leq1$
-
$F(x_0+0)=F(x_0)$,其中 $F(x_0+0)=\lim_{x\rightarrow x_0^+} F(x)$。相应的,函数图中,间断点的右边为实心点,左边为空心点(如上图)
注意,以上表示满足 右连续,但不满足左连续,这与分布函数定义中的 $F_X(x)=P{X\leq x}$ 有关。在有的教科书中,$F_X(x)=P{ X<x }$,则满足左连续不满足右连续。
对于满足以上性质的函数都可以看作分布函数。
$F_1(x), F_2(x)$ 是两个分布函数,问 $F_1(x)\cdot F_2(x)$,$F_1(x)+F_2(x)$ 是否是分布函数?
$F_1(x)\cdot F_2(x)$是,而$F_1(x)+F_2(x)$,因为后者不满足第2条性质。
例题:设一个醉汉游离于 A,B 两点,AB之间距离为3个单位,该醉汉停在AB间任一子区间的概率于区间长度成正比,设他落在离 A 点距离 $X$ 远处,求 $X$ 的分布函数。
解:
由题意,$P(0\leq X \leq 3)=1$
故当$x<0$时,$F(x)=0$,当$X\geq3$时,$F(x)=1$
设比例系数为k,则 $P(0\leq X \leq 3)=3k=1$,得 $k=1/3$
当 $0\leq X<3$时,$F(x)=P(X\leq x)$$=P(X<0)+P(0\leq X\leq x)=0+\frac{1}{3}x$
从而分布函数为:
$$
F(x)=P(X\leq x)
\begin{cases}
0, x<0\\
x/3, 0\leq x\leq3\\
1, x\geq3
\end{cases}
$$
离散型随机变量
定义 离散型随机变量
若随机变量的取值为有限个或可数个1,则称 $X$ 为离散型随机变量。
分布律
离散型随机变量的概率分布律就是一个表格,表格包含:
- 随机变量的所有可能取值
- 每个取值的概率($p_k\geq 0$,$\sum_k p_k=1$)
除了表格外,有时也用 $P(X=x_k)=p_k$ 来表示。

投一枚骰子,直到投出6为止,问投出次数的概率
$P(X=k)=(\frac{5}{6})^{k-1} \frac{1}{6}$
分布律与分布函数之间的转换:分布律的每个 $X$ 值对应分布函数的间断点 $x$,$P$ 对应间断点处的值减上一间断点的值。
 </center> </center>
|
|
二项分布
如果一个随机变量 $X$ 取值为 $0,1,2,\cdots,n$,且 $P(X=k)=C_n^k p^k (1-p)^{n-k}$,$k=0,1,2,\cdots,n$,则 $X$ 称为二项分布(Binomial),记为 $X\sim B(n,p)$
(也可定义为:n重贝努里实验2中,事件A 出现的次数 X 服从二项分布)
特殊地,
- 如果 $n=1$,则称为两点分布(01分布),其分布律满足 $P(X=k)=p^k(1-p)^{1-k}, k=0,1$
- 如果随机变量 $X$ 只取常数,则称 $X$ 为退化分布(单点分布),其分布律满足 $P(X=c)=1$
定理
若 $X\sim B(n,p)$,则由下式成立:
- 事件A发生的次数在 k1,k2 之间:$P(k_1\leq X \leq k_2)=\sum_{k=k_1}^{k_2}B(k;n,p)$
- 事件A发生的次数至少为 r 的概率,$P(X\geq r)=1-\sum_{k=0}^{r-1}B(k;n,p)$
定理
设 $X\sim B(n,p)$,令 $m=\text{Int}[(n+1)p]$
则 $k=m$ 时,$B(k;n,p)$ 的值最大,并且有 $B(k;n,p)=B(k-1;n,p)$
证明
例题:从塘中捞起 100 条鱼,做上记号后,放回池塘,过一段时间后再捞起 80 条,发现其中有 2 条,求鱼的总数 N
解:设 $X$ 为80条鱼中,有记号的鱼的条数,则 $X\sim B(80, \frac{100}{N})$,则 X 最可能发生的是 $m=[(80+1)\times\frac{100}{N}]=2$
解 $(80+1)\times\frac{100}{N}\approx2$ 得 $N=4050$
相比之下,高中生物方法解出的是:4000
泊松分布
若离散型随机变量 $X$ 的分布律为:$P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}$,$k=0,1,2,\cdots$,其中 $\lambda\geq0$ 是常数。称这分布为 泊松分布(Poisson),记为 $X\sim\text{Pois}(\lambda)$
注意请记住这条泰勒展式:$e^\lambda=\sum_{k=0}^{+\infty} \dfrac{\lambda^k}{k!}$,后面会经常用到。
定理 泊松定理
当 $n>10$,$p<0.1$ 时,二项分布 $X\sim B(n,p)$ 可以用泊松分布 $X\sim \text{Pois}(np)$ 近似,即:
\[C_n^kp^k(1-p)^{n-k}\approx\frac{e^{-\lambda}\lambda^k}{k!}, 其中, \lambda\approx np\]几何分布
若 $X$ 满足 $P(X=k)=p(1-p)^{k-1}$,$k=1,2,3,\cdots$,其中 $0<p<1$,则称 $X$ 服从 几何分布(Geometric),记为 $X\sim \text{Geom}(p)$ 或 $X \sim G(p)$
几何分布的用途:在n重贝努里实验中,实验进行到某种结果出现第一次为止,此时的实验总次数服从几何分布。
以上列出的分布要熟记。