\(\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \end{align*}\)
离散时间信号
时域描述
虽然在信号与系统中已经学过离散时间信号,但我们依然要说一下。
模拟信号(Analog Signal)表示为 $x_a(t)$,其中 $t$ 为连续量;数字信号 $x[n]$ 可以看做对模拟信号的采样,其中 $n$ 为离散量。所以我们将数字信号用序列表示,称作 样本,即:
\[x[n] = \{ \cdots, x[-1], \belowarrow{x}[0], x[1],\cdots \}\]箭头 $\uparrow$ 指示 $t=0$ 时刻的样本值。
下面说几个概念:
序列可以分解为 实序列 和 虚序列:$x[n]=x_\text{re}[n]+jx_\text{im}[n]$
序列的长度可以为有限长或无限长。对于有限长序列,其 长度 或 时宽 $N=N_右-N_左+1$。我们可以通过 补零 的方法将有限长序列变为无限长序列。
如果序列在 $n \leq N_1$ 时为 0,则为 右边序列,若 $N_1\geq 0$ 则称为 因果序列。反之在 $n \geq N_2$ 时为 0,则为 左边序列,若 $N_2\leq 0$ 则称为 反因果序列。关于这个我们会在后面进一步讨论。
有时候时域分析不方便,我们会对时域样本进行变换。假设 $\bd{x}$ 是序列在时域对应的向量,$\bd{X}$ 则是序列在变换域对应的向量,定义可逆矩阵 $\bd{D}$,满足:
\[正变换:\bd{X}=\bd{Dx}\\ 逆变换:\bd{x}=\bd{D}^{-1}\bd{x}\]信号的强度
之前学过信号的能量和功率,这里要讲得“强度”类似。我们一般用 $\L_p$ 范数 来衡量:
\[\|x\|_p = \left( \sum_{n=-\infty}^{+\infty} \big|\, x[n]\,\big|^p \right)^{1/p}\]$p$ 常取 $1,2,\infty$。范数有一些性质,比如:$|x|_2 \leq |x|_1$,证明过程如下:
\[\|x\|_1 = \sum_{n=-\infty}^{+\infty} \big|\, x[n]\,\big|\\ \|x\|_2 = \sqrt{ \sum_{n=-\infty}^{+\infty} \big|\, x[n]\,\big|^2 }\\ 对两式平方:\\ \begin{align} \|x\|_1^2 &= (\cdots +|x[-1]|+|x[0]|+|x[1]|+\cdots)^2\\ &= \|x\|_2^2+\sum_{i\neq j} |x[i]\cdot x[j]| \end{align}\]另一个常用的性质是:$\|x \|\infty = \vert x\vert\text{max}$(容易通过极限来证明)
范数在其他定义中也有用到,比如:
- 均方根值(rms):$\text{rms}=\dfrac{\|x\|_2}{\sqrt{N}}$
- 均方误差(MSE):$\text{MSE}=\frac{1}{N} (\|y[n] - x[n] \|_2)^2$
- 相对误差:$\text{E}_\text{rel} = \dfrac{\| y[n]-x[n]\|_2}{\|x[n]\|_2}$
norm(x,1) %L1范数
norm(x,2) %L2范数
norm(x,inf) %L_infinity范数
基本序列
下面列出了一些基本序列,和对应的matlab代码。下面所有的 $n$ 的取值范围都是 $(-\infty,+\infty)$,以后凡是未标范围的都默认是 $(-\infty,+\infty)$。
单位样本序列 Unit Sample Sequence
\[\delta[n]= \begin{cases} 1, & n=0\\ 0, & n\neq 0 \end{cases} =\{ \cdots, 0, 0, \belowarrow{1}, 0, 0, \cdots\}\]function [x,n] = impseq(n0,n1,n2)
% Generates x[n] = delta(n-n0); n1<=n<=n2
n = [n1:n2];
x = [(n-n0) == 0];
end
单位阶跃序列 Unit Step Sequence
\[u[n]= \begin{cases} 1, & n\geq 0\\ 0, & n\lt 0 \end{cases} =\{ \cdots, 0, 0, \belowarrow{1}, 1, 1, \cdots\}\]function [x,n] = stepseq(n0,n1,n2)
% Generates x[n] = u(n-n0); n1<=n<=n2
n = [n1:n2];
x = [(n-n0)>=0];
end
指数序列 Exponential Sequence
实指数的形式比较简单:$x[n]=A a^n,\;\; A,a\in \mathbb{R}$;将 $A,a$ 的定义域换成复数域就得到复指数:
\[\alpha = e^{(\sigma_0+j\omega_0)}, \quad A = \vert A \vert e^{j\phi}\\ x[n] = \vert A \vert e^{j\phi} e^{(\sigma_0+j\omega_0)n}\]有的人喜欢将虚部和实部分开:
\[\begin{align} x[n] &= \vert A \vert e^{\sigma_0n} e^{j(\omega_0n+\phi) }\\ &=\vert A \vert e^{\sigma_0n} \big[ \cos(\omega_0n+\phi) + j \sin(\omega_0n+\phi)\big] \end{align}\]这样可以很清晰的看出,实部和虚部都是衰减/增长的三角序列。至于什么时候增长,什么时候衰减,以及周期问题,请去复习 SCUTEEE-信号与系统-信号
function [x,n] = expseq(A,a,n1,n2)
% Generates x[n] = A*exp(a*n); n1<=n<=n2
n = [n1:n2];
x = A*exp(a*n);
end
正弦序列 Sinusoidal Sequence
说是正弦序列,但其实我们用余弦函数来表示:
\[x[n] = A \cos(\omega_0n+\phi)\]$A$,$\omega_0$,$\phi$ 分别称为 振幅,归一化角频率 和 相位(准确来讲是初相位)
正弦序列可以分解为 同相分量(in-phase) 与 正交分量(quadrature):
\[\begin{align} x[n] &=x_i[n]+x_q[n]\\ &=A\cos \phi \cos (\omega_0 n) - A \sin \phi \sin(\omega_n) \end{align}\]在通信原理中可能会接触一个 IQ调制,其中 I 和 Q 就是指同相与正交。想了解更多,可以去看 详解IQ调制
>> n = [0:10];
>> x = 3*cos(2*pi*n+pi/3)
关于正弦序列的周期问题,我们在 SCUTEEE-信号与系统-信号 已经讨论过,在此仅列举结论:
- 若 $\omega_0 N = 2\pi r$($N,r$ 为正整数),则为周期的。$N$ 的最小取值为基本周期
- 在 $[0,\pi]$ 内,振荡频率随 $\omega_0$ 增加而增加,在 $[\pi,\pi]$ 内,振荡频率随 $\omega_0$ 增加而减小。$\pi$ 称为 折叠频率
矩形窗序列 Rectangular Window
\[w_R[n] = \begin{cases} 0, & n<N_1\\ 1, & N_1 \leq n \leq N_2\\ 0, & n>N_2 \end{cases}\]function [x,n] = recwindow(n1,n2,n3,n4)
% Generates rectangular window
n = [n3:n4];
x = [n>=n1|n<=n2];
end
序列的运算
简单运算
| 运算 | 器件 | 表达式 |
|---|---|---|
| 乘积 multiplication | 调制器 | $y[n]=x_1[n]\cdot x_2[n]$ |
| 标量积 scaling | 乘法器 | $y[n]=A x_[n]$ |
| 相加 addition | 加法器 | $y[n]=x_1[n]+ x_2[n]$ |
| 延迟/超前 shifting | 延时器 | $y[n]=x[n-N]$($N<0$ 为延迟,$N>0$ 为超前) |
| 反转(折叠)folding | $y[n]=x[-n]$ |
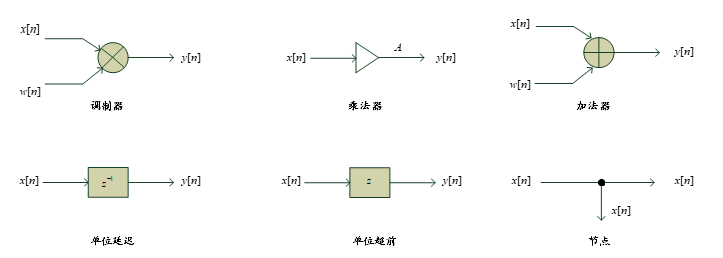
在实现这几个运算时,要考虑序列不等长,以及序列范围不一致的情况。Matlab 代码如下:
function [y,n] = sigadd(x1,n1,x2,n2)
% implements y(n) = x1(n) + x2(n)
% y = sum sequence over n, which includes n1 and n2
% x1 = first sequence over n1
% x2 = second sequence over n2
% 加法器
n = min(min(n1),min(n2)):max(max(n1),max(n2));
y1 = zeros(1,length(n));
y2 = y1;
y1(find((n>=min(n1))&(n<=max(n1))==1))=x1;
y2(find((n>=min(n2))&(n<=max(n2))==1))=x2;
y = y1+y2;
end
function [y,n] = sigmult(x1,n1,x2,n2)
% implements y(n) = x1(n)*x2(n)
% y = product sequence over n, which includes n1 and n2
% x1 = first sequence over n1
% x2 = second sequence over n2
% 乘法器
n = min(min(n1),min(n2)):max(max(n1),max(n2));
y1 = zeros(1,length(n));
y2 = y1;
y1(find((n>=min(n1))&(n<=max(n1))==1))=x1;
y2(find((n>=min(n2))&(n<=max(n2))=x2))=x2;
y = y1.*y2
end
function [y,n] = sigshift(x,m,k)
% implement y(n) = x(n-k)
% 延时器
n = m+k;
y = x;
end
function [y,n] = sigfold(x,n)
% implements y(n) = x(-n)
% 反转
y = fliplr(x);
n = -fliplr(n);
end
卷积和 Convolution
\[y[n] = \sum_{k-\infty}^{+\infty} x[n-k]h[k]=x[n]\circledast h[n]\\ 使用 \circledast 以免与共轭 {}^* 混淆\]卷积和的相关性质请参考:卷积和与卷积积分 - SCUTEEE
function [y,ny] = conv_m(x,nx,h,nh)
%Modified convolution routine for signal processing
% [y,ny] = conv_m(x,nx,h,nh)
% [y,ny] = convolution result
% [x,nx] = first signal
% [h,nh] = second signal
nyb = nx(1)+nh(1);
nye = nx(length(x)) + nh(length(h));
ny = [nyb:nye];
y = conv(x,h);
end
抽样率转换
抽样率转换实际上就是内插 or 再抽取。假如 $x[n]$ 是抽样率为 $F_T$(Hz)的序列,现在将其转化为抽样率为 $F’_T$(Hz)的序列 $y[n]$,其比值 $R = \dfrac{F’_T}{F_T}$ 定义为 抽样转换比
- 若 $R>1$,说明抽样率提高,该转化系统为 内插器
- 若 $R<1$,说明抽样率降低,该转化系统为 抽取器
要实现抽样率转换,最简单的就是进行 上抽样(up-sampling) 和 下抽样(down-sampling) 运算。这两个运算方法很简单:上抽样就是在两个样本之间补零,下抽样就是去掉某些样本。具体如下:
\[\begin{align} &上抽样:x_u[n] = \begin{cases} x[n/L], & n=0,\pm L, \pm 2L\\ 0, &其他 \end{cases}\\ &下抽样:y[n]=x[nM] \end{align}\]经过上述两个变换后,抽样率变为了 $L$ 倍或 $1/M$ 倍。所以上抽样器也称为 抽样率扩展器,下抽样器也称为 抽样率压缩器。
有限长序列的反转与平移
有时候,我们希望有限长序列在做完运算后,定义域不改变。所以我们规定限长序列的反转与平移运算如下:假如定义域为 $0,1,\cdots,N-1$,则:
- 反转:$y[n]=x[(-n)\mod N]$ 写作 $x[\langle -n \rangle_N ]$ 1
- 平移:$y[n]=x[(n-n_0) \mod N]$ 写作 $x[\langle n-n_0 \rangle_N ]$
如果我们将样本放在一个圆周上,那么平移就相当于转动这个圆周,而反转则相当于对这个圆周以 $x[0]$ 对应的直径进行镜像。因此,这两个运算又称作 圆周时间反转(circular shift) 和 圆周平移(circular time-reversal)
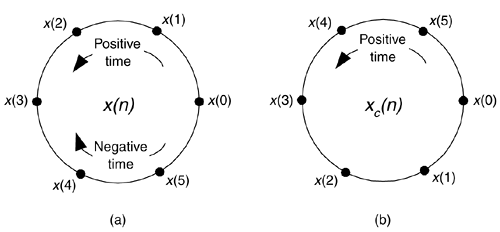
扩展:圆周卷积 circular convolution
\[g[n]\,Ⓝ\,h[n] = \sum_{k=0}^{N-1} g[k]h[\langle n-k \rangle_N ]\\ 相当于:\\ \begin{bmatrix} y[0] \\ y[1] \\ \cdots \\y[N-1] \end{bmatrix} = \begin{bmatrix} h[0] & h[N-1] & \cdots & h[1]\\ h[1] & h[0] & \cdots & h[2]\\ \vdots & \vdots & & \vdots\\ h[N-1] & h[N-2] & \cdots & h[0] \end{bmatrix} \begin{bmatrix} g[0] \\ g[1] \\ \cdots \\g[N-1] \end{bmatrix}\]序列的分类
因为懒得打字,所以就抄了别人的博文
-
基于对称性
若满足 $x[n] = x^*[-n]$ ,称为 共轭对称序列;
若满足 $x[n] = - x^*[-n]$ ,称为 共轭反对称序列。
- 实共轭对称序列称为偶序列
- 实共轭反对称序列称为奇序列
- 任何复序列都能表示成共轭对称部分 $x_\text{cs}[n]$ 与共轭反对称部分 $x_\text{ca}[n]$ 之和,其中: \(x_\text{cs}[n]=\frac{1}{2}(x[n]+x^*[-n])\\ x_\text{ca}[n]=\frac{1}{2}(x[n]-x^*[-n])\)
- 周期信号 与 非周期信号。周期信号用 $\tilde{x}[n]$ 表示
- 能量信号 与 功率信号
- 其他序列 有界序列、绝对可和序列、平方可和序列、n点序列等,都是有某些特征的序列。
信号的相关
自相关与互相关
为了比较两个信号的相似程度,我们可以将两个信号相减:
\[\sum_{n=-\infty}^{+\infty} (x[n]-y[n-\ell])^2\\ =\sum_{n=-\infty}^{+\infty} (x^2[n]-2x[n]y[n-\ell]+y^2[n-\ell])\]如果越相似,那么差值就越小。注意到式中,$x^2[n]$ 与 $y^2[n-\ell]$ 都是正值,要让差值越小,那么只能让 $x[n]y[n-\ell]$ 越大。于是我们定义 相关 如下:
\[互相关:r_{xy}[\ell] = \sum_{n=-\infty}^{+\infty} x[n]y[n-\ell]\\ 自相关:r_{xx}[\ell] = \sum_{n=-\infty}^{+\infty} x[n]x[n-\ell]\\\]其中,$\ell$ 称为 时滞。自相关和互相关的最大值所对应的 $\ell$ 就是信号最相似的部分。显然,自相关应该在 $\ell=0$ 处取最大值,证明如下:
\[\begin{align} &\sum_{n=-\infty}^{+\infty} (x[n]-x[n-\ell])^2\\ =& \sum_{n=-\infty}^{+\infty} x^2[n] -2 \sum_{n=-\infty}^{+\infty} x[n]x[n-\ell] + \sum_{n=-\infty}^{+\infty} x^2 [n-\ell]\\ =& r_{xx}[0] - 2 r_{xx}[\ell]+r_{xx}[0]\\ \geq& 0 \end{align}\\ \therefore r_{xx}[\ell] \leq r_{xx}[0] = \mathscr{E}_x\]书上有个更为巧妙,适用范围更广的证法:
\[\begin{align} &\sum_{n=-\infty}^{+\infty} (ax[n]+y[n-\ell])^2\\ =& a^2\sum_{n=-\infty}^{+\infty} x^2[n] +2a \sum_{n=-\infty}^{+\infty} x[n]y[n-\ell] + \sum_{n=-\infty}^{+\infty} y^2 [n-\ell]\\ =& a^2 r_{xx}[0] + 2a r_{xy}[\ell]+r_{yy}[0]\\ \geq& 0 \end{align}\\ \therefore \begin{bmatrix} a & 1 \end{bmatrix} \begin{bmatrix} r_{xx}[0] & r_{xy}[\ell]\\ r_{xy}[\ell] & r_{yy}[0] \end{bmatrix} \begin{bmatrix} a \\ 1 \end{bmatrix} \geq 0\\ \Rightarrow \begin{bmatrix} r_{xx}[0] & r_{xy}[\ell]\\ r_{xy}[\ell] & r_{yy}[0] \end{bmatrix} 半正定\\ \therefore \begin{vmatrix} r_{xx}[0] & r_{xy}[\ell]\\ r_{xy}[\ell] & r_{yy}[0] \end{vmatrix} \geq 0\\ -\sqrt{r_{xx}[0]r_{yy}[0]} \leq r_{xy}[\ell] \leq \sqrt{r_{xx}[0]r_{yy}[0]}\]这个证明给出了 $r_{xy}[\ell]$ 的上下界,并且在 $y[n]=x[n]$ 时,就得到我们上面自相关的结论。
相关的归一化形式
由于相关不仅会受到相似程度的影响,也会受信号本身的能量影响,因此我们需要对相关进行归一化,即让相关函数的值落在 $[-1,1]$ 之间。注意到 $r_{xy}[\ell]$ 的上下界是 $\sqrt{r_{xx}[0]r_{yy}[0]}$,将自相关和互相关除以这个值就能得到它们的归一化形式
\[\rho_{xx}[\ell] = \frac{r_{xx}[\ell]}{\mathscr{E}_x}\\ \rho_{xy}[\ell] = \frac{r_{xx}[\ell]}{\sqrt{\mathscr{E}_x \mathscr{E}_y}}\]经过归一化后,$\vert \rho_{xx}[\ell] \vert\leq 1$,$\vert \rho_{xy}[\ell] \vert\leq 1$,与信号本身的大小无关。
本章练习题
2.24(a) 证明:当定义域为 $[0,+\infty)$ 时,因果实序列 $x[n]$ 可以从其偶部 $x_\text{ev}[n]$ 中完全恢复出来;而当定义域为 $(0,+\infty)$ 时,因果实序列 $x[n]$ 可以从其奇部 $x_\text{od}[n]$ 中完全恢复出来。
证:$x[n]$ 的偶部和奇部可以表示为:
$$
x_\text{ev}[n] = \frac{x[n]+x[-n]}{2}\\
x_\text{od}[n] = \frac{x[n]-x[-n]}{2}
$$
由前提条件,在 $(-\infty,0)$ 上 $x[n]=0$,所以有:
$$
x_\text{ev}[n] = \frac{x[n]}{2},\; n>0\\
x_\text{od}[n] = \frac{x[n]}{2},\; n>0\\
\therefore x[n]=2x_\text{ev}[n]=2x_\text{od}[n],\; n>0
$$
再考虑 $x=0$ 处,显然 $x[0]=x[-0]$,所以有:
$$
x_\text{ev}[0] = x[0]\\
x_\text{od}[0] = 0\quad\\
$$
综上,可以从偶部得到因果序列在 $n\geq 0$ 处的值,可以从虚部得到因果序列在 $n >0$ 处的值。证毕。
另外,在推导过程中并未考虑序列的实部与虚部,说明该结论对复序列一样成立。
2.24(b) 证明:因果复序列 $y[n]$ 可以从其共轭对称部分 $y_\text{cs}[n]$ 中完全恢复出来;$y[n]$ 可以从其共轭反对称部分 $y_\text{ca}[n]$ 中完全恢复出来。
证:共轭对称部分与共轭反对称部分可以表示为:
$$
\begin{align}
y_\text{cs}[n] &= \frac{1}{2}(y[n]+y^*[-n])\\
&=\frac{y_\text{re}[n]+y_\text{re}[-n]}{2}+j \frac{y_\text{im}[n]-y_\text{im}[-n]}{2}\\
&=y_\text{re,ev}[n]+y_\text{im,od}[n]\\
y_\text{ca}[n] &= \frac{1}{2}(y[n]-y^*[-n])\\
&=\frac{y_\text{re}[n]-y_\text{re}[-n]}{2}+j \frac{y_\text{im}[n]+y_\text{im}[-n]}{2}\\
&=y_\text{re,od}[n]+y_\text{im,ev}[n]
\end{align}
$$
根据上一题 2.24(a) 的结论:可以从偶部得到因果信号在 $n\geq 0$ 处的值,可以从虚部得到因果信号在 $n >0$ 处的值。我们可以推导出如下结论:
(1) 可以从 $y_\text{cs}[n]$ 得到 $y_\text{re}[n]$ 在 $n\geq 0$ 处的值,以及 $y_\text{im}[n]$ 在 $n>0$ 处的值。
(2) 可以从 $y_\text{ca}[n]$ 得到 $y_\text{re}[n]$ 在 $n>0$ 处的值,以及 $y_\text{im}[n]$ 在 $n\geq 0$ 处的值。
因此,当所有 $n>0$ 时,因果复序列 $y[n]$ 可以从其共轭对称部分 $y_\text{cs}[n]$ 中完全恢复出来,也可以从其共轭反对称部分 $y_\text{ca}[n]$ 中完全恢复出来。证毕。
2.39(d)(e) 求以下信号的基本周期:
$$
\begin{align}
\text{(d)}\;\tilde{x}[n]&=6\sin(0.15\pi n)-\cos(0.12\pi n+0.1\pi)\\
\text{(e)}\;\tilde{x}[n]&=\sin(0.1\pi n + 0.75\pi)-3\cos(0.8\pi n+0.2\pi)+\cos(1.3\pi n)
\end{align}
$$
解:求出各部分的基本周期,再求最小公倍数。
对于 $\text{(d)}$,其各部分的基本周期分别为:$T_1=\frac{2\pi}{0.15\pi}\times3=40$,$T_2=\frac{2\pi}{0.12\pi}\times 3=50$,则 $T=\frac{40\times50}{\text{GCD}(40,50)}=200$
对于 $\text{(d)}$,其各部分的基本周期分别为:$T_1=\frac{2\pi}{0.1\pi}=20$,$T_2=\frac{2\pi}{0.8\pi}\times 2=5$,$T_3=\frac{2\pi}{1.3\pi}\times 13=20$,则 $T=20$
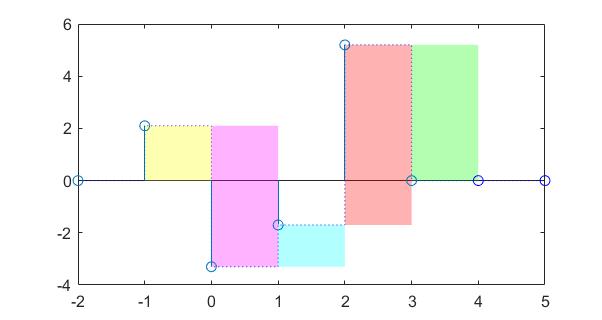
2.44 用单位阶跃序列 $\mu[n]$ 表示 $x[n]=\{2.1,\belowarrow{-3.3},-1.7,5.2\}$
解:仿照杜阿美积分,我们可以写出: $$ \begin{align} x[n]=&\mu[n+1](x[-1]-0)\\ &+\mu[n+0](x[0]-x[-1])\\ &+\mu[n-1](x[1]-x[0])\\ &+\mu[n-2](x[2]-x[1])\\ &+\mu[n-3](0-x[2])\\ =&2.1\mu[n+1]-5.4\mu[n+0]+1.6\mu[n-1]\\ &+6.9\mu[n-2]-5.2\mu[n-3] \end{align} $$
2.51 连续时间信号 $x_a(t)=\cos \Omega_o t$ 在 $t=nT$ 抽样,$-\infty\lt n\lt +\infty$,生成离散时间序列 $x[n]=x_a(nT)=\cos (\Omega_o nT)$。当 $T$ 取咩值时 $x[n]$ 是一个周期序列?若 $\Omega_o=30\text{rad}$ 且 $T=\pi/6\text{s}$,$x[n]$ 的基本周期是多少?
解:若 $x[n]$ 是一个周期序列,则要满足 $\dfrac{2\pi}{\Omega_o T}=\dfrac{N}{r}$,$N,r\in \mathbb{N}$,即 $T=k\dfrac{2\pi}{\Omega_o}且 T\neq 0$,$k\in\mathbb{R}$
若 $\Omega_o=30\text{rad}$ 且 $T=\pi/6\text{s}$,则 $x[n]=\cos(5 \pi n)$,基本周期 $T=\dfrac{2\pi}{5\pi}\times 5=2$
-
我们用 $\langle n \rangle_N$ 表示 $n \mod N$ ,某些教材(比如 Oppenheim 的教材)也将取模运算写作:$((n))_N$ ↩