设计 IIR 滤波器
总的来说,就是利用模拟滤波器来设计数字滤波器,根据转换的方法不同,分为:
- 冲激响应不变法
- 双线性变换法
冲激响应不变法
变换原理:数字滤波器的脉冲响应为 $h[n]$,模拟滤波器的冲激响应为 $h_a(t)$,冲激响应不变就是指这俩在 $t=nT$ 时相同,即:
\[h[n]=h_a(t) \Big\vert_{t=nT}\\ H(z)\Big\vert_{z=e^{sT}} = \hat{H}_a (s)=\frac{1}{T}\sum_{k=-\infty}^{+\infty} H_a \left( s-j\frac{2\pi}{T}k \right)\]映射关系如下图(多对一):
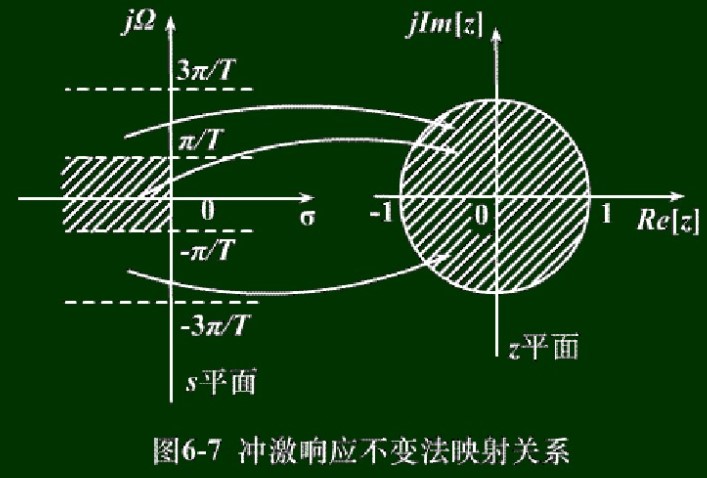
由于数字滤波器相当于对模拟滤波器在时域上采样,频域上进行周期延拓,所以只适合设计低通和带通滤波器(避免混叠)。这种方法的优点是时域逼近良好,且相位保持线性关系。
模拟到数字的转换过程如下:
\[H_a(s) \rightarrow h_a(t) \rightarrow h_a(nT) \rightarrow h(n) \rightarrow H(z)\]- $H_a(s)=\sum_{k=1}^N \dfrac{A_k}{s-p_k}$
- $h_a(t)=\sum_{k=1}^N A_k e^{p_k t}u(t)$
- $h(n)=h_a(nT)=\sum_{k=1}^N A_k (e^{p_kT})^n u(n)$
- $H(z)=\sum_{n=-\infty}^\infty h(n)z^{-n}$ $=\sum_{n=0}^{\infty}\sum_{k=1}^N A_k \left( e^{p_kT}\right)^n z^{-n}$ $=\sum_{k=1}^N \frac{A_k}{1-e^{p_k T}z^{-1}}$
最终我们得到:
\[H_a(s)=\sum_{k=1}^N \frac{A_k}{s-p_k} \rightarrow H(z)=\sum_{k=1}^N \frac{A_k}{1-e^{s_kT}z^{-1}}\]综上,设计过程是这样的:
- 选择 $T$,然后求出对应的模拟频率: \(\Omega = \frac{\omega}{T}\)
- 根据 $\Omega_p$,$\Omega_s$,$R_p$,$A_s$ 设计模拟滤波器
- 将 $H_a(s)$ 展开为部分分式的形式: \(H_a(s)=\sum_{k=1}^{N} \frac{R_k}{s-p_k}\)
- 将模拟转化为数字: \(H(z)=\sum_{k=1}^N \frac{R_k}{1-e^{p_k T}z^{-1}}\)
双线性变换法
双线性变换就是用了不同的 $s\rightarrow z$ 转换方法:
\[s=\frac{1-z^{-1}}{1+z^{-1}}\\ z=\frac{1+s}{1-s}\]它的映射关系如下(一对一):
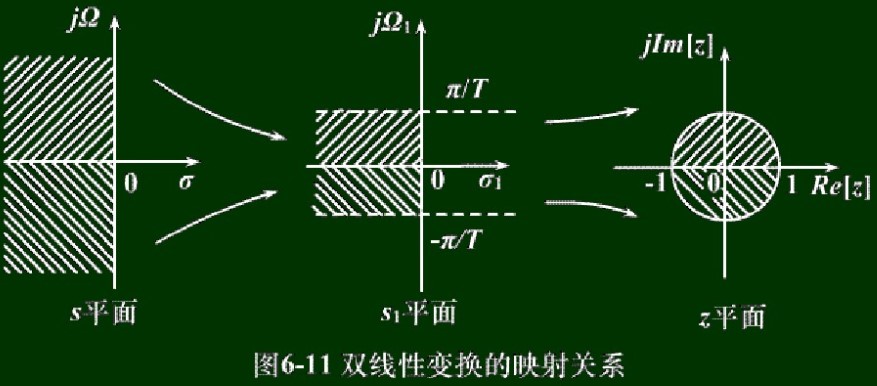
这种变换的优点就是:s平面与z平面是单值变换,所以避免了混叠。缺点就是:除了零频率附近,模拟频率 $\Omega$ 与数字频率 $\omega$ 之间非线性,因此要求幅度响应应该为分段常数型,否则会产生畸变。
公式的推导过程如下:
我们先将模拟频率 $\Omega=[-\infty,+\infty]$ 压缩到 $\Omega_1=[-\pi/T,\pi/T]$
\[\Omega=\tan \frac{\Omega_1 T}{2}\]然后再将 $\Omega_1$ 映射到 $z$(就是冲激响应不变法中的过程):
\[z=e^{s_1 T}\]将两个结合起来,有:
\[\begin{aligned} \Omega&=\tan \frac{\Omega_1 T}{2}\\ &=\frac{\sin\frac{\Omega_1 T}{2}}{\cos\frac{\Omega_1 T}{2}}\\ &=\frac{e^{j\frac{\Omega_1 T}{2}}-e^{-j\frac{\Omega_1 T}{2}}}{2j}\bigg/ \frac{e^{j\frac{\Omega_1 T}{2}}+e^{-j\frac{\Omega_1 T}{2}}}{2} \end{aligned}\] \[\begin{aligned} s&=j\Omega\\ &=\frac{e^{j\frac{\Omega_1 T}{2}}-e^{-j\frac{\Omega_1 T}{2}}}{e^{j\frac{\Omega_1 T}{2}}+e^{-j\frac{\Omega_1 T}{2}}}\\ &=\frac{1-e^{-s_1 T}}{1+e^{-s_1T}}\\ &=\frac{1-z^{-1}}{1+z^{-1}} \end{aligned}\]推导完毕。从上面推导中,可以注意到模拟频率 $\Omega$ 与数字频率 $\omega=\Omega_1 T$ 的对应关系不是线性的,而我们希望它越接近线性越好,于是我们进行一个拉伸操作:
\[\Omega = c \cdot \tan \frac{\omega}{2}\\ s = c \frac{1-z^{-1}}{1+z^{-1}}\\ z=\frac{c+s}{c-s}\]若要求在低频处有比较明确的(线性)对应关系,那么:
\[\Omega_1 \approx \Omega = c \cdot \tan \frac{\Omega_1 T}{2} \approx c \cdot \frac{\Omega_1T}{2}\\ \Rightarrow c = \frac{2}{T}\]从而双线性变换可以进一步写为:
\[s = \frac{2}{T} \left(\frac{1-z^{-1}}{1+z^{-1}}\right)\]这正是课本中介绍的双线性变换。
若要求在某个频率 $\Omega_c\leftrightarrow \omega_c$ 处有比较明确的(线性)对应关系,那么:
\[\Omega_c = c \cdot \tan \frac{\omega_c}{2}\\ \Rightarrow c = \Omega_c \cot \frac{\omega_c}{2}\]式中的 $\Omega_c, \omega_c$ 是自己设定的。
习题
9.3 设一个低通滤波器 $H(z)$ 的通带波纹为 $\delta_p$,阻带波纹为 $\delta_s$。若将两个 $H(z)$ 级联,则波纹是多少?若 n 个级联呢?
解:系统级联则幅度响应相乘,故阻带波纹为:$\delta_s^n$,通带波纹为 $(1+\delta_p)^n-1$
对通带波纹的一点讨论:课本中对 $\delta_p$ 的定义是这样的:
在通带内,要求幅度响应以误差 $\pm \delta_p$ 逼近 1,即 $1-\delta_p \leq \vert G(e^{j\omega}) \vert 1+\delta_p$
级联后,通带内的最大值为:$(1+\delta_p)^n$,偏离 1 的幅度为 $2\delta_p+\delta_p^2$;最小值为 $(1-\delta_p)^2$,偏离 1 的幅度为 $2\delta_p-\delta_p^2$
由于 $2\delta_p+\delta_p^2>2\delta_p-\delta_p^2$,根据定义应该取较大的那个作为误差。
9.16 设一个模拟低通滤波器 $H_a(z)$ 的截止频率为 $\Omega_c$,以 $t=nT$ 进行采样,得到 $H_1(e^{j\omega})$ 和 $H_2(e^{j\omega})$,其中,$T_1=3\pi/2\Omega_c$,$T_2=\pi/\Omega_c$。令 $G_1=H_1+H_2$,$G_2 = H_1-H_2$,请画出 $G_1,G_2$ 的图像,并判断类型。
解:最高频为 $f_c=\frac{\Omega_c}{2\pi}$,由采样定理,不混叠的条件是 $f_T>\frac{\Omega_c}{\pi}$. 因为 $\frac{1}{T_1}< f_T=\frac{1}{T_2}$,所以 $H_1(e^{j\omega})$ 存在混叠,而 $H_2(e^{j\omega)}$ 无混叠。图像如下:
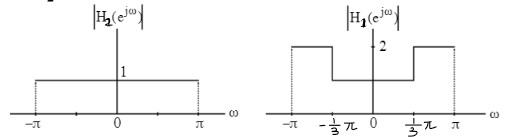
从而 $G_1,G_2$ 的图像如下:
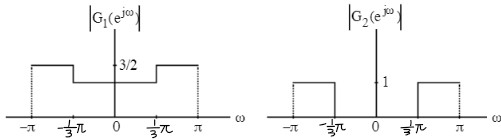
9.27 一个 3dB 截止频率为 $\omega_c$ 的二阶低通 IIR 滤波器为:
$$
G_\text{LP} (z)=\frac{0.3404(1+z^{-1})^2}{1+0.1842 z^{-1}+0.1776 z^{-2}}
$$
请通过低通到低通的谱变换设计一个 $\hat{\omega}_c = 0.27 \pi$ 的低通滤波器 $H_\text{LP}(z)$
解:就是代公式。
$$
\lambda = \frac{\sin \left( \frac{\omega_c-\hat{\omega}_c}{2} \right)}{\sin \left( \frac{\omega_c+\hat{\omega}_c}{2} \right)}=0.4434
$$
$$
H_\text{LP} = G_\text{LP}(z^{-1}=\frac{\hat{z}^{-1}-\lambda}{1-\lambda \hat{z}^{-1}}) = \frac{0.1055+0.2109 \hat{z}^{-1} + 0.1055 \hat{z}^{-2}}{0.9532-0.8239\hat{z}^{-1}+0.2925 \hat{z}^{-2}}
$$