\(\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \end{align*}\)
讲真我觉得这个实验老师没讲什么有用的。
实验要求
- 编写一个频率可调、声音大小可调的函数,能产生20Hz到20kHz的响度可调的单频声音信号
-
编写一个频率范围可调, 幅度/时长可调的函数, 能产生在20Hz到20KHz的范围内的线性调频信号,信号形式如下:
\[x[nT]=\exp (j2\pi f_c nT + j \pi \mu (nT)^2)\]$f_c$ 是中心频率,$T$ 是采样间隔,$\mu$ 是调频率
- 将产生的线形调频信号作为输入,并做线性延时相加运算,然后利用互相关对延时信号进行延时估计,观察不同频宽、时长线性调频信号的估计精度差别。
实验过程
要求1. 很简单,用正弦函数即可,我们要注意的是采样率。matlab 中 sound 函数对采样率的规定如下:
sound(y) % 以默认采样率 2^13=8192 赫兹向扬声器发送音频信号 y。
sound(y,Fs) % 以采样率 Fs 向扬声器发送音频信号 y。
sound(y,Fs,nBits) % 对音频信号 y 使用 nBits 的采样位数。
%附:采样率最小为 1000Hz
所以容易写出 soundgen(sound generator):
function y = soundgen(A,f,n,fs)
y = A*sin(2*pi*f*n/fs);
sound(y, fs);
end
我们来产生一个中央C(do~🎵):
soundgen(1,261.6,1000,1000);
让我们来唱一下小星星(莫扎特的小星星变奏曲🎵):
little_star_right=[1 1 5 5 6 6 5 5 4 4 3 3 2 3 1];
little_star_left=[1 8 10 8 11 8 10 8 9 7 8 6 4 5 1];
notes = [1 3 5 6 8 10 12 13 15 17 18 20];
for note = 1:15
r = 220*2.^((notes(little_star_right(note))+2)./12);
l = 220*2.^((notes(little_star_left(note))-10)./12);
soundgen(1,r,1024,2048);
soundgen(0.3,l,1024,2048);
pause(0.5)
end
可以听一下原曲:
还是差很多,因为钢琴还有一些泛音啥的,所以听起来会好听很多。
等会儿,不是要弄自相关吗?怎么跑偏了???让我们一边听着小星星一边写下面的内容吧!
下一个是调频信号,题目中给的公式是一类特定的调频信号,叫作 线性调频(Linear Frequency Modulated)信号,其定义式如下:
\[x(t)=\exp (j2\pi f_c t + j \pi \mu t^2)\]通过对相位进行微分,可以求出其频率为:
\[\frac{1}{2\pi} \frac{\dif \theta}{\dif t} = f_c+\mu t\]其频率会随时间变大而变大,$\mu$ 可以看做是“斜率”。
function [x,xn] = LFM(A, fc, u, T, n1, n2)
%generate signal: A*exp(j*2*pi*fc*n*T+j*pi*u*(n*T)^2)
% A = amplitude
% fc = center frequence
% u = slope
% T = sampling time
% n1 = start time
% n2 = end time
xn=[n1:n2];
x=A*exp(1i*2*pi*fc*xn*T+1i*pi*u*(xn*T).^2);
end
%为了方便看,相位就从0开始
[x,xn]=LFM(1, 0, 100, 0.001, 0, 300);
plot(xn,real(x),'b')
%为了好玩,可以听一下这个声音
%[x,xn] = LFM(1, 20, 100, 0.001, 0, 3000);
%sound(real(x),1000)
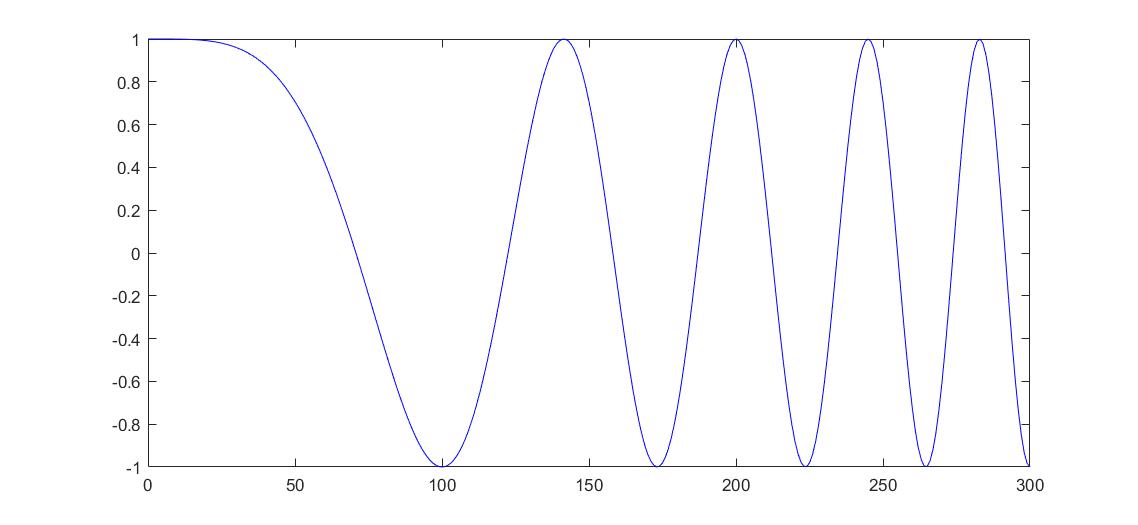
顺便提一句,由于频率是不断升高的,所以采样频率到后面是不够的,如果后面出现了一些“周期性”的图案,可以调小 $\mu$ 或调大采样频率。
然后我们对信号进行线性延时相加:(利用之前定义过的 sigadd 和 sigshift,这里再写一次)
function [y,n] = sigadd(x1,n1,x2,n2)
% implements y(n) = x1(n) + x2(n)
% y = sum sequence over n, which includes n1 and n2
% x1 = first sequence over n1
% x2 = second sequence over n2
% 加法器
n = min(min(n1),min(n2)):max(max(n1),max(n2));
y1 = zeros(1,length(n));
y2 = y1;
y1(find((n>=min(n1))&(n<=max(n1))==1))=x1;
y2(find((n>=min(n2))&(n<=max(n2))==1))=x2;
y = y1+y2;
end
function [y,n] = sigshift(x,m,k)
% implement y(n) = x(n-k)
% 延时器
n = m+k;
y = x;
end
我们对信号分别延时 50 和 -100,然后将两个延时信号相加:
[y1, yn1] = sigshift(x, xn, 50);
[y2, yn2] = sigshift(x, xn, -100);
[y yn] = sigadd(y1*0.5,yn1,y2*2,yn2);
然后终于迎来最重要的自相关啦!matlab 中已经有现成的 xcorr 可用,想要挑战自我的同学也可以根据定义写一个自相关。
function [z,zn] = myxcorr(x,xn,y,yn)
% calculate xcorr(x,y)
%将两个信号补零到相同长度
n = min(min(xn),min(yn)):max(max(xn),max(yn));
x1 = zeros(1,length(n));
y1 = x1;
x1(find((n>=min(xn))&(n<=max(xn))==1))=x;
y1(find((n>=min(yn))&(n<=max(yn))==1))=y;
z = xcorr(x1,y1);
zn = [-length(n)+1:length(n)-1];
end
[z,zn]=myxcorr(y,yn,x,xn);
plot(zn,z);
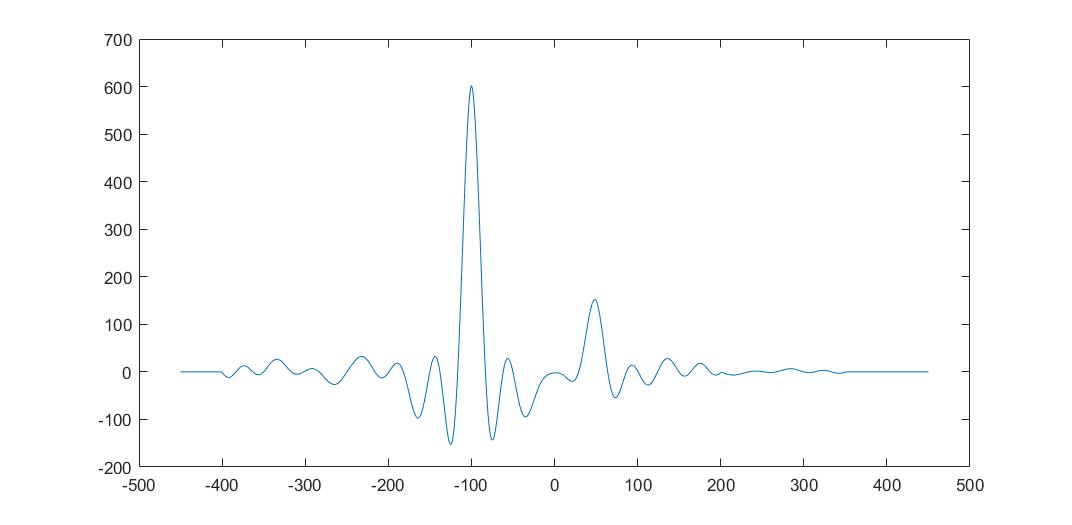
从图中可以估算信号分别时移了 -100 和 50,与实际吻合。
[x,xn]=LFM(1, 0, 500, 0.001, 0, 300); plot(xn,real(x),’b’) [y1, yn1] = sigshift(x, xn, 50); [y2, yn2] = sigshift(x, xn, -100); [y yn] = sigadd(y10.5,yn1,y22,yn2); [z,zn]=myxcorr(y,yn,x,xn); plot(zn,z);